Конспект урока «Теорема Пифагора» по геометрии для 8 класса
План – конспект урока геометрии в 8 классе
по теме «Теорема Пифагора»
Учитель: Платонова Валентина Николаевна
Цель урока: изучить доказательство теоремы Пифагора и научить решать
задачи на её применение.
Задачи:
• образовательные (формирование познавательных УУД):
формирование умения учащихся применять теорему Пифагора в реальных
ситуациях, знаково–символические и логические действия, осознанно и
произвольно строить свои высказывания;
• развивающие (формирование регулятивных УУД):
умение обрабатывать информацию и ранжировать её по указанным
основаниям; планировать свою деятельность в зависимости от конкретных
условий; контроль и оценка процесса и результатов деятельности;
• воспитательные (формирование коммуникативных и личностных УУД):
умение слушать и вступать в диалог, участвовать в коллективном обсужде-
нии проблем, воспитывать ответственность и аккуратность.
Тип урока: урок изучения нового материала.
Планируемые результаты:
Личностные УУД:
Формировать учебную мотивацию, адекватную самооценку, необходимость
приобретения новых знаний.
Метапредметные УУД:
Регулятивные:
понимать учебную задачу урока, осуществлять решение учебной задачи
под руководством учителя, определять цель учебного задания, контроли-
ровать свои действия в процессе его выполнения, обнаруживать и исправ-
лять ошибки, отвечать на итоговые вопросы и оценивать свои достижения.
Познавательные:
формировать навыки применения теоремы Пифагора, вырабатывать навыки
решения задач по данной теме, научить составлять план решения задач.
Коммуникативные:
воспитывать любовь к математике, коллективизм, уважение друг к другу,
умение слушать, дисциплинированность, самостоятельность мышления.
Формы работы: фронтальная, индивидуальная, парная.
Оборудование: проектор, экран, презентация PowerPoint, учебник
Геометрия 7-9 кл. (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк,
И.И.Юдина).
Методы обучения:
• Репродуктивный (стимулирование учебной деятельности)
• Наглядный
• Проблемно-поисковый
• Эвристическая беседа
Структура урока.
-
Организационный момент (1 мин.)
2. Этап проверки домашнего задания. (7 мин.)
3. Этап актуализации темы и мотивация.(3 мин.)
4. Изучение нового материала.(7 мин.)
5. Практическая часть. Решение задач.(7 мин.)
6. Физкультминутка.(2 мин.)
7. Проверочная работа.(5 мин.)
8. Решение старинной задачи (из «Арифметики» Л.Ф.Магницкого).(5 мин.)
9. Подведение итогов урока. (2 мин.)
10. Домашнее задание. (1 мин.)
Ход урока.
1. Организационный момент. (1 мин.)
Цель: подготовить учащихся к работе на уроке.
Деятельность учителя:
Приветствует учащихся, проверяет готовность к уроку, организует внима-
ние, включает в деловой ритм учащихся, задаёт настрой на урок. Цитирует
девиз урока «Чем больше я знаю, тем больше умею»
. Деятельность учащихся:
Приветствуют учителя, отвечают на вопросы, делают выводы.
Формируемые УУД:
Личностные: смыслообразование
Познавательные: целеполагание
Коммуникативные: планирование учебного сотрудничества
2. Этап проверки домашнего задания. (7 мин.)
Цель: проверить правильность и осознанность выполнения домашнего
задания всеми учащимися, установить пробелы в знаниях, совершенство-
вать знания и умения учащихся о фигурах квадрат, прямоугольный треу-
гольник и свойствах их элементов.
Деятельность учителя: Координирует деятельность учащихся, организует
устную работу учащихся.
Деятельность учащихся: рассказывают решение задач по готовому черте-
жу, отвечают на вопросы учителя. Идёт индивидуальная и фронтальная
работа.
Формируемые УУД:
Познавательные: анализ, синтез, обобщение, классификация, подведение
под понятие, осознанное и произвольное построение речевого высказы-
вания.
Регулятивные: выполнение пробного учебного действия, фиксирование
индивидуального затруднения в пробном действии, волевая саморегуляция
в ситуации затруднения
Личностные: формирование ценностных ориентиров и смыслов учебной
деятельности на основе развития познавательных интересов, учебных
мотивов.
Коммуникативные: выражение своих мыслей с достаточной полнотой и
точностью, аргументация своего мнения, учёт разных мнений учащихся.
Вопросы классу:
а) Рассказать решение задач по готовому чертежу.
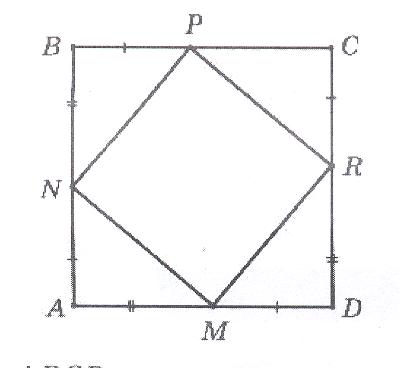 1.Дано: АВСD – квадрат;
1.Дано: АВСD – квадрат;
АN=BP=CR=DM, NB=PC=RD=MA.
Доказать, что NPRM – квадрат.
2.Дано: NPRM – квадрат, ABCD –
квадрат; AN=3 cм, NB=4cм.
Найти сторону квадрата NPRM.
б) Устная работа.
1.Сторона квадрата равна a cм. Найдите его площадь.
2.Сторона квадрата равна a + b. Как найти его площадь?
3.Какой треугольник называется прямоугольным? Как называются его
стороны?
4.В треугольнике MPO угол О прямой. Назовите его гипотенузу и катеты.
5.Как найти площадь прямоугольного треугольника? 3. Этап актуализация темы и мотивация.(3 мин.)
Цель: Сформулировать теорему Пифагора.
Деятельность учителя: Учитель начинает беседу с проблемной задачи по бу-
дущей теме урока, возвращаясь к задаче 2 предыдущего этапа урока.
Деятельность учащихся: Учащиеся отвечают на вопросы учителя, подгото-
вленный заранее ученик читает доклад о Пифагоре (историческая справка).
Формируемые УУД:
Познавательные: анализ, синтез, обобщение, классификация, подведение
под понятие, осознанное и произвольное построение речевого высказы-
вания.
Регулятивные: выполнение пробного учебного действия, волевая
саморегуляция в ситуации затруднения
Личностные: формирование ценностных ориентиров и смыслов учебной
деятельности на основе развития познавательных интересов, учебных
мотивов.
Коммуникативные: выражение своих мыслей с достаточной полнотой и
точностью, аргументация своего мнения, учёт разных мнений учащихся.
а) Беседа учителя. Основной вопрос: решена задача 2, известны стороны
прямоугольного треугольника. Какую связь можно установить между
гипотенузой и катетами этого треугольника? (Возможна помощь со сто-
роны учителя)
б) Подготовленный заранее ученик делает сообщение о Пифагоре.
Историческая справка.
Пифагор родился в 576 г. до н.э. на острове Самос, расположенном в
Эгейском море. Четыре раза подряд Пифагор был олимпийским чемпио-
ном. По совету Фалеса 22 года Пифагор набирался мудрости в Египте.
Во время завоевательных походов попал в плен, был продан в рабство и
10 лет жил в Вавилоне. Вернувшись на родину, Пифагор организовал Пи-
фагорейский орден – школу философов и математиков. Во время народно-
го восстания в 496 г. до н.э. он был убит в уличной схватке.
4. Изучение нового материала.(7 мин.)
Цель: учить оперировать знаниями, развивать гибкость использования
знаний при выстраивании логической цепочки доказательства
теоремы Пифагора.
Деятельность учителя: Слова учителя: теорема Пифагора занимает в
геометрии особое место. На её основе можно вывести или доказать
большинство теорем. А ещё она замечательна тем, что сама по себе не
очевидна. Сколько ни смотри на прямоугольный треугольник, никак не
увидишь, что его стороны связывает простое соотношение: квадрат
гипотенузы равен сумме квадратов его катетов.
Деятельность учащихся: Самостоятельное изучение учащимися
доказательства теоремы Пифагора (стр.130 учебника).
Формируемые УУД:
Познавательные: извлечение необходимой информации из текстов; анализ,
синтез, сравнение, обобщение, аналогия; подведение под понятие; постро-
ение логической цепи рассуждений, доказательство; структурирование
знаний.
Регулятивные: фиксация индивидуального затруднения, волевая
саморегуляция в ситуации затруднения.
Коммуникативные: выражение своих мыслей с достаточной полнотой и
точностью.
Личностные: осознание ответственности.
5. Практическая часть. Решение задач.(8 мин.)
Цель: закрепить изученный материал, научиться правильно оформлять
решение задач на применение теоремы Пифагора, запомнить новое.
Деятельность учителя: проектирует задачи на экран, оказывает помощь
ученикам, испытывающим затруднения при выполнении практической
работы.
Деятельность учащихся: решают задачи на применение теоремы, проверяют
решения заданий 2 и 3 одноклассниками, исправляют и дополняют свои
решения в тетрадях.
Формируемые УУД:
Познавательные: анализ, синтез, сравнение, обобщение, моделирование,
использование знаково-символических средств, выполнение действия по
алгоритму, осознанное и произвольное построение речевого высказывания.
Регулятивные: контроль полученного результата, коррекция
полученного результата, элемент волевой саморегуляции и осознание
качества и уровня усвоения..
Личностные: планирование учебного сотрудничества с учителем и
одноклассниками.
Коммуникативные: умение самостоятельно анализировать свои действия
Задания классу:
Задание 1.(работа в парах)
Вычислите, если возможно:
а) сторону АС треугольника АВС;
б) сторону МN треугольника KMN;
в) диагональBD квадрата ВСDF;
г) сторону KP треугольника KPR;
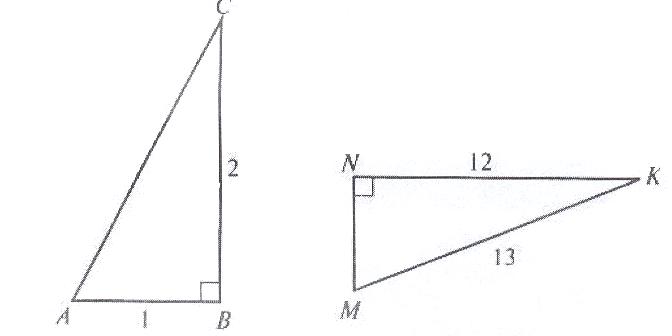
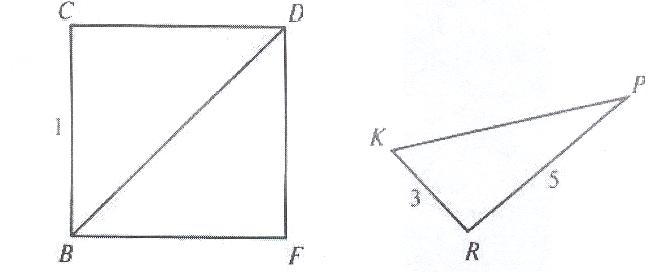
Ответы: а) ![]() ; б) 5; в)
; б) 5; в) ![]() ; г) сторону треугольника вычислить нельзя.
; г) сторону треугольника вычислить нельзя.
Замечание. Учитель, направляя работу учащихся, должен обратить
внимание на то, что увидели ли учащиеся, что в задаче 1,г не хватает
данных для решения. Неясно, какой вид имеет треугольник KPR.
В такой ситуации теорема Пифагора, конечно, неприменима.
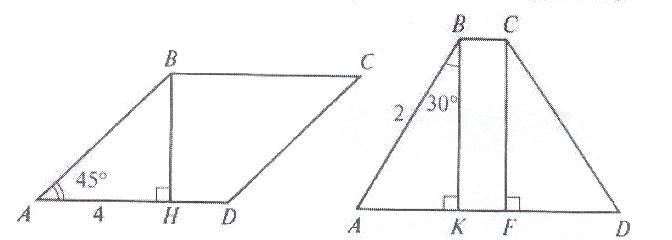
Задание 2.(Один ученик готовит решение на 1 обороте доски)
Найдите сторону CD параллелограмма ABCD. (Ответ: 4![]() .)
.)
Задание 3. ( Другой ученик готовит решение на 2 обороте доски)
Вычислите высоту CF трапеции ABCD. (Ответ: ![]() .)
.)
6.Физкультминутка.(2 мин.)
Цель: снять напряжение в зрительной системе учащихся.
Деятельность учителя:
Почти 90% всей информации человек воспринимает глазами. Если устают
глаза, снижается наше внимание и активность. Давайте перед следующим
заданием дадим отдых глазам и себе.
1.Закройте глаза на несколько секунд, сильно напрягая глазные мыщцы,
затем раскройте их, расслабив мышцы. Повторите 3-4 раза.
2.Посмотрите на переносицу и задержите взор. Затем посмотрите вдаль.
Повторите 3-4 раза.
3.Медленно наклоняйте голову: вперёд – влево – вправо – назад. Повтори-
те 3-4 раза.
4.Поморгайте несколько раз глазами, не напрягая мышц. Сделайте глубо-
кий вздох и медленный выдох.
Деятельность учащихся: выполняют упражнения, отдыхают.
Формируемые УУД:
Регулятивные: элемент волевой саморегуляции
Личностные: осознание ценности здоровья.
7. Проверочная работа.(5 мин.)
Цель: запомнить новое.
Деятельность учителя: проектирует задание на экран, оказывает помощь
учащимся, испытывающим затруднения при выполнении задания.
Деятельность учащихся: Выполняют самостоятельно задание.
Формируемые УУД:
Познавательные: анализ, синтез, сравнение, обобщение, использование
знаково-символических средств, выполнение действий по алгоритму.
Регулятивные: контроль полученного результата, коррекция полученно-
го результата, элемент волевой саморегуляции и осознание качества и уровня
усвоения.
Личностные: планирование учебного сотрудничества с учителем и
одноклассниками.
Коммуникативные: умение самостоятельно анализировать свои действия.
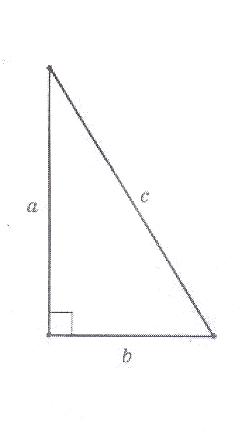
Задание. В прямоугольном треугольнике a, b – катеты, с – гипотенуза.
Заполните таблицу.
| b | c | |
| 30 |
| 50 |
| 1 | 1 | |
| 12 | 15 | |
| 8 | 10 |
8. Решение старинной задачи (из «Арифметики» Л.Ф.Магницкого).
( 5 мин.)
Цель: применить новое.
Деятельность учителя: проектирует задачу на экран, даёт время для само-
стоятельного решения задачи, верное решение обязательно оценивает по
высшему баллу.
Деятельность учащихся: Решают самостоятельно задачу.
Формируемые УУД:
Познавательные: анализ, синтез, обобщение, моделирование, преобразо-
вание модели, самостоятельное создание алгоритмов деятельности,
доказательство.
Регулятивные: контроль полученного результата, коррекция полученно-
го результата, элемент волевой саморегуляции и осознание качества и уровня
усвоения.
Личностные: планирование учебного сотрудничества с учителем и
одноклассниками.
Коммуникативные: умение самостоятельно анализировать свои действия
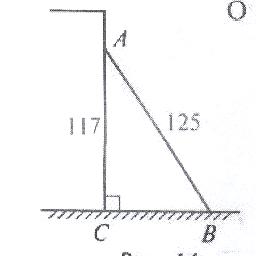
Задача. Случися некоему человеку к стене лествицу прибрати, стены же тоя
высота есть 117 стоп. И обрете лествицу долготою 125 стоп. И ведати
хощет, колико стоп сея лествицы нижний конец от стены отстояти
имать.
Решение. Треугольник АВС – прямоугольный. Пусть ВС=х стоп, тогда по
теореме Пифагора АС![]() + СВ
+ СВ![]() = АВ
= АВ![]() , 117
, 117![]() + х
+ х![]() = 125
= 125![]()
х![]() = 125
= 125![]() – 117
– 117![]() ,
,
х![]() = (125 – 117)(125 +117),
= (125 – 117)(125 +117),
х![]() = 8 ∙ 242, х = 44.
= 8 ∙ 242, х = 44.
Ответ: 44 стопы.
9. Подведение итогов урока (2мин.).
Цель: зафиксировать новое содержание, изученное на уроке: теорема
Пифагора и её применение при решении задач.
Деятельность учителя: выставляет оценки за активную работу на уроке и хорошие результаты практической работы, задаёт вопросы классу по итогам урока.
Деятельность учащихся: оценить собственную деятельность на уроке, поблагодарить одноклассников, которые помогли получить результат урока, зафиксировать неразрешённые затруднения как направления будущей учебной деятельности.
Формируемые УУД:
Познавательные: рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности, адекватное понимание причин успеха или неуспеха
Коммуникативные: аргументация своего мнения, планирование учебного сотрудничества
Вопросы учителя классу:
1.О чём сегодня на уроке шла речь?
2. Какие вы испытали трудности и как из них вышли?
3.Где в жизни использует теорему Пифагора обычный человек?
10. Домашнее задание(1 мин)
Цель: задать дозированное домашнее задание.
Деятельность учителя: задаёт дозированное домашнее задание и коммен-
тирует его.
Деятельность учащихся: учащиеся записывают домашнее задание в днев-
ники.
Формируемые УУД:
Познавательные: самостоятельное создание способов решения проблем
творческого характера.
Регулятивные: планирование, саморегуляция.
Личностные: проявление готовности к самообразованию и самовоспитанию.
Коммуникативные: умение слушать и вступать в диалог.
Задание на дом: обязательно п.54, с.129-131, № 486(б,в).
Дополнительно: найти и выучить другое доказательство теоремы Пифа-
гора (их более 100), это будет вашим индивидуальным проектом;
выяснить, что такое «пифагоровы штаны».
Здесь представлен конспект к уроку на тему «Теорема Пифагора», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Геометрия (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

