Конспект урока «Различные способы доказательства теоремы Пифагора» по геометрии для 8 класса
Ход урока:
Здравствуйте, садитесь. Меня зовут Людмила Александровна, я рада всех Вас видеть (слайд 1).
Пребудет вечной истина, как скоро
Её познает слабый человек!
И ныне теорема Пифагора верна,
Как и в его далёкий век.
Немецкий писатель-романист Шамиссо.
Эти слова посвящены одной из известнейших теорем математики. Теореме Пифагора (слайд 2).
Перед Вами портрет великого Пифагора (слайд 3). Он известен как древнегреческий философ и педагог. Пифагор – это прозвище, данное ему за красноречие («Пифагор» - значит «убеждающий речью»). Сам он ничего не писал, а все его мысли записывали ученики. Он был первым, кто назвал свои рассуждения о смысле жизни философией.
Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с его теоремой. Пожалуй даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах». Причина такой популярности – её простота, красота и значимость. В самом деле, теорема Пифагора проста и имеет огромное значение, потому что она применяется в различных областях, а тот факт, что существует около 500 различных доказательств этой теоремы, свидетельствует о её широком применении. Теорема Пифагора заслужила место в «Книге рекордов Гиннеса», как получившая наибольшее число доказательств.
Тема нашего урока «Различные способы доказательства теоремы Пифагора».
Как вы считаете, чем мы с Вами будем заниматься на уроке?
(учащиеся формулируют цель урока).
Конечно же каждый из вас понимает, что за один урок невозможно рассмотреть 500 доказательств, но еще с двумя доказательствами теоремы, помимо рассмотренного вами ранее мы познакомимся.
Вы уже рассмотрели эту теорему, поэтому давайте повторим (слайд 4).
1. К каким треугольникам можно применить теорему Пифагора?
2. Как звучит теорема Пифагора?
3. Чему равна гипотенуза прямоугольного треугольника, катеты которого равны 6см и 8см?
4. Верно ли, что в прямоугольном треугольнике любой из катетов меньше гипотенузы?
5. Гипотенуза прямоугольного треугольника равна 5см, катет 3см. Найти длину второго катета?
Проводится обсуждение и проверка по ответам.
Учитель: Молодцы, мы с вами очень хорошо справились с заданием.
А знаете ли Вы, что доказательство теоремы Пифагора считалось в кругах учащихся средних веков очень трудным и называлось иногда «ослиным мостом» или «бегством убогих», потому что некоторые слабые ученики бежали от геометрии. Они, не пытаясь понять доказательство, просто его зазубривали. Поэтому, возникали различные карикатуры, которые сопровождали доказательство теоремы (слайд 5).
Я думаю, что мы с Вами сможем преодолеть все трудности, и не будем спасаться бегством при рассмотрении доказательств этой теоремы.
Сейчас мы с Вами проведем небольшую лабораторную работу. (Откройте, пожалуйста, тетради, запишите число и классная работа).
(кто-то работает у доски).
Вам нужно (слайд 6):
-
Начертить в тетрадях прямоугольный треугольник со сторонами 3; 4 и 5 см;
-
Построить на катетах и гипотенузе квадраты;
-
Найти площади построенных квадратов.
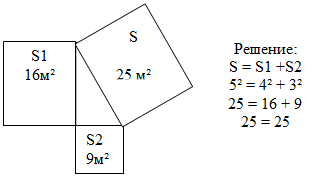
Как вы считаете, доказали мы, что квадрат гипотенузы равен сумме квадратов его катетов?
Оказывается, что мы с Вами рассмотрели один из частных случаев доказательства теоремы Пифагора (слайд 7).
У каждого из Вас лежат листочки с таблицами, которые называются Пифагоровыми тройками (слайд 8).
Пифагоровы тройки
| 3 | 5 | 6 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | |
| b | 4 | 12 | 8 | 24 | 40 | 60 | 84 | 112 | 144 | 180 |
| c | 5 | 13 | 10 | 25 | 41 | 61 | 85 | 113 | 145 | 181 |
Эти числа обладают рядом интересных особенностей, познакомимся с ними: один из «катетов» должен быть кратным трём;
один из «катетов» должен быть равен четырём;
одно из пифагоровых чисел должно быть кратно пяти.
С помощью предложенных таблиц решите следующие задачи (слайд 9).
«Всё есть число», «Числа правят миром» - изречения Пифагорам (слайд 10). Он считал, что через числа можно выразить все закономерности мира. Нужно отметить, что все Пифагорейцы обожествляли числа и геометрические фигуры. Давайте немного отвлечемся и поговорим о числовой мистике.
Число 1 означало огонь,
2 – землю,
3 – воду,
4 – воздух,
Сумма этих чисел 10 – весь мир,
5 – любовь.
Проведем физкультминутку и получим заряд энергии от чисел.
Раз, два – встать пора,
Три, четыре – руки шире,
Пять, шесть – тихо сесть,
Семь, восемь – лень отбросим.
Э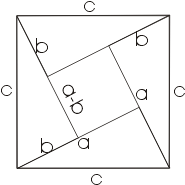 нергией мы зарядились, а сейчас рассмотрим еще одно геометрическое доказательство теоремы (слайд 11). Изобразите пожалуйста чертеж в своих тетрадях.
нергией мы зарядились, а сейчас рассмотрим еще одно геометрическое доказательство теоремы (слайд 11). Изобразите пожалуйста чертеж в своих тетрадях.
Этот способ доказательства рассмотрел индийский математик Бхаскара. В пояснение к доказательству он написал только одну строчку: «Смотри!» Другие ученые предположили, что он выражал площадь квадрата, построенного на гипотенузе, как сумму площадей треугольников и площади квадрата. Давайте, восстановим это доказательство. Кто желает выступить в роли учёного?
Получаем: c²=4ab/2+(a-b)²
c=2ab+a²-2ab+b²
c²=a²+b²
Как вы считаете, доказали мы, что квадрат гипотенузы равен сумме квадратов его катетов?
Очень хорошо. Мы надеемся, что ты станешь великим математиком.
А теперь давайте решим ещё несколько задач (слайд 12).
Домашнее задание (слайд 13): Найти интересное, на ваш взгляд, доказательство теоремы Пифагора и красочно его оформить. Лучшими работами оформим стенд.
Итог:
-
Скажите, пожалуйста, сколько всего существует доказательств теорем Пифагора?
-
А сколько доказательств теорем теперь знаете Вы?
-
Сформулируйте ещё раз теорему.
На следующих уроках вы рассмотрите практическое применение рассмотренной нами теоремы.
По окончанию урока я попрошу каждого из Вас подойти к доске и прикрепить карточку с одним из предложенных Вам чисел. «10»(целый мир), если урок понравился; «5»(любовь) - если, что-то не понравилось и «1»(огонь) - если урок не понравился.
(слайд 14). Благодарю Вас всех за урок, мне было очень приятно с вами сотрудничать.
Здесь представлен конспект к уроку на тему «Различные способы доказательства теоремы Пифагора», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Геометрия (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

