государственное бюджетное общеобразовательное учреждение Самарской области средняя общеобразовательная школа с. Троицкое

муниципального района Сызранский Самарской области

Открытый урок по геометрии в 8 классе

на тему

Разработал и провёл учитель математики

Пуговкина Татьяна Викторовна

с. Троицкое

2013-2014 учебный год

Конспект урока по геометрии.

Класс: 8.

Дата проведения: 15.12.2013г.

Время проведения: 11.20-12.05 час.

Тема урока: Теорема Пифагора.

Цель урока: Изучить теорему Пифагора.

Задачи: 1. Познакомить учащихся с теоремой Пифагора и способами её доказательства.

2. Воспитание ответственности, самостоятельности, умений оценивать свои знания, учиться работать на доверии, самопроверке.

3. Формирование организованности, ответственности, дисциплинированности, культуры общения учащихся.

План урока:

I. Подготовительный этап.

II. Изучение теоремы.

III. Закрепление теоремы.

IV. Заключительный.

Форма проведения урока: урок-путешествие.

Оборудование урока: ПК, экран, презентация урока (слайды- карта Средиземного моря, портрет Пифагора, вопросы и задания), модель для доказательства теоремы Пифагора, пентаграммы с иголками, карточки с заданием на дом.

Ход урока.

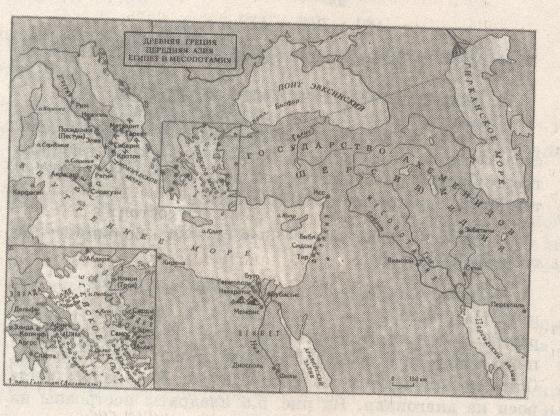
На экране появляется карта Средиземного моря (в течение урока слайды сменяют друг друга).

У

А

читель: Сегодня у нас необычный урок. Попробуем совершить путешествие на остров Самос, расположенный в Эгейском море. Мы узнаем , чем интересен этот остров, и какие «математические события» там происходили. Путешествовать будем на сверхскоростном самолёте, ведь время у нас ограничено – 45 минут. Итак, мы в самолёте. Проверим вашу готовность.

1. Подготовительный этап.

Повторение. Актуализация знаний.

1. Фронтальный опрос.

(По рисунку 1)

1. Как называется фигура, изображённая на рисунке 1?

2. Какой треугольник называется прямоугольным?

3. Как называются его стороны?

4. Что такое гипотенуза?

5. Ч

   С

   В

   то такое катет?

6. Назовите по рисунку гипотенузу и катеты.

7. Как найти площадь прямоугольного треугольника? Рис. 1

8. Катеты прямоугольного треугольника равны

16см и 10см. Чему равна его площадь?

В

С

(По рисунку 2)

1) Какая фигура изображена на рисунке 2?

2) Что такое квадрат?

3) Как найти его площадь?

4

D

) Сторона квадрата 8см. Найдите его площадь.

5

А

) Сторона квадрата равна а+в. Как найти его площадь?

Рис. 2

У

9

читель: Теперь в путь! Наш самолёт находится на высоте 9 км.

На земле мы преодолели расстояние 12 км.

Какой путь пролетел самолёт в воздухе с момента взлёта (рис. 3)?

12

Рис. 3

2. Практическая работа.

С

В

b

N

C

a

формулируем задачу в общем виде: известны катеты прямоугольного треугольника. Найти длину его гипотенузы. Пока мы не можем решить эту задачу. Давайте рассмотрим её на модели (рис. 4), а выводы запишем в тетрадях.

В

a

озьмём прямоугольный треугольник с катетами а и b

и гипотенузой с и достроим его до квадрата со стороной а+ b.

П

M

b

c

лощадь его равна .

Р

c

анее мы доказали, что четырёхугольник KMNP- квадрат.

Найдём площадь квадрата ABCD:

b

c

.

Т

P

c

огда

a

D

K

А

b

a

А

.

Рис. 4

II. Изучение теоремы.

Сделаем вывод: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Доказательство этого факта принадлежит древнегреческому учёному Пифагору.

Вернёмся к рассматриваемой задаче. Применим теорему Пифагора для вычисления длины гипотенузы.

Дано: АВС, В= 90 , а=9км, b=12км.

Найти: с

Решение: Так как по условию АВС- прямоугольный, то по теореме Пифагора имеем:

, с=15.

Ответ. Самолёт пролетел путь, равный 15км.

III. Закрепление теоремы.

1. Историческая справка.

Учитель: Мы с вами прибыли на остров Самос, и нас встречают экскурсоводы. Экскурсоводы рассказывают о жизни Пифагора, пифагорейской школе и истории открытия теоремы.

1 экскурсовод. Здравствуйте, ребята! На нашем острове в VI в. до н.э. жил величайший древнегреческий математик Пифагор. Известно, что родился он на острове Самос, расположенном в Эгейском море. По совету Фалеса 22 года Пифагор набирался мудрости в Египте. В Вавилон он попал не по своей воле. Во время завоевательных походов на Египет войска полководца Камбиза взяли Пифагора в плен и продали в рабство. Он более 10 лет жил в Вавилоне, изучал древнюю культуру и достижения науки разных стран.

2 экскурсовод. Вернувшись на Родину, Пифагор организовал пифагорейский орден и школу философов и математиков. Туда принимались с большими церемониями после долгих испытаний. В школе существовал декрет, по которому авторство всех математических работ приписывалось самому Пифагору. В школе была очень серьёзная дисциплина. Главным безоговорочным аргументом в научных спорах были слова «сам сказал». После этого дискуссия прекращалась.

1 экскурсовод. Излюбленной геометрической фигурой пифагорейцев была пентаграмма или пифагорейская звезда. При встрече они рисовали её на песке, тем самым приветствуя друг друга. Пентаграмма служила им паролем и была символом здоровья и счастья.

2 экскурсовод. Наконец, последний штрих к портрету учёного. Он был четыре раза подряд олимпийским чемпионом. В пятисотых годах до нашей эры Пифагор был убит в уличной схватке во время народного восстания. После смерти его ученики окружили имя своего учителя множеством легенд, так что правду о Пифагоре установить невозможно.

2. Решение задач.

У

3

4

читель: По традиции этого острова всякий прибывающий на него сдаёт экзамен на право быть пифагорейцем. Для этого выполните устно следующие упражнения.

1. Дан прямоугольный треугольник (рис. 5).

Вычислите длину гипотенузы.

2. В

   x

   треугольнике АВС (рис. 6)

вычислите длину стороны ВС.

Рис. 5

B

Решить в тетрадях задачу:

Н

10

айти диагонали прямоугольника, если

его стороны равны 3/4 м и 4/7 м.

1

x

экскурсовод (обращаясь к классу). Вы становитесь

членами нашего ордена. Теперь каждый из вас носит

почётное имя пифагорейца и получает пентаграмму,

к

A

C

ак символ здоровья и счастья.

(

6

Всем раздаются пентаграммы.)

Рис. 6

IV. Заключительный.

Учитель: Мы возвращаемся домой. Подведём итог нашего путешествия. Теорема Пифагора – одна из главных теорем геометрии. Значение её состоит в том, что из неё или с её помощью можно вывести большинство теорем геометрии и решить множество задач. Этой теореме даже посвящены стихи.

2 экскурсовод читает стихи Шамиссо.

О теореме Пифагора.

Суть истины вся в том, что нам она – навечно,

Когда хоть раз в прозрении её увидим свет,

И теорема Пифагора через столько лет

Для нас, как для него, бесспорна, безупречна.

На радостях богам был Пифагором дан обет:

За то, что мудрости коснулся бесконечной,

Он сто быков заклал, благодаря предвечных;

Моленья и хвалы вознёс он жертве вслед.

С тех пор быки, когда учуят, тужась,

Что к новой истине людей опять подводит след,

Ревут остервенело, так что слушать мочи нет,

Такой в них Пифагор вселил навеки ужас.

Быкам, бессильным новой правде противостоять,

Что остаётся? – Лишь глаза закрыв, реветь, дрожать.

Задание на дом:

Каждому учащемуся раздаются карточки с домашним заданием:

1. § 3, п. 54 (по учебнику Л.С. Атанасян и др.)

2. Индивидуальные задания по карточкам: В изображённом прямоугольном треугольнике измерить катеты и вычислить длину гипотенузы.

3. №№ 483(а), 484(а).

Список использованной литературы

• 1. Учебник «Геометрия 7-9 классы», авт. Л.С. Атанасян и др., М. «Просвещение», 2010

• Коллекция рисунков в сети Интернет

• Стихотворение Шамиссо «О теореме Пифагора»