Презентация "История геометрии" – проект, доклад
Презентацию на тему "История геометрии" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 25 слайд(ов).
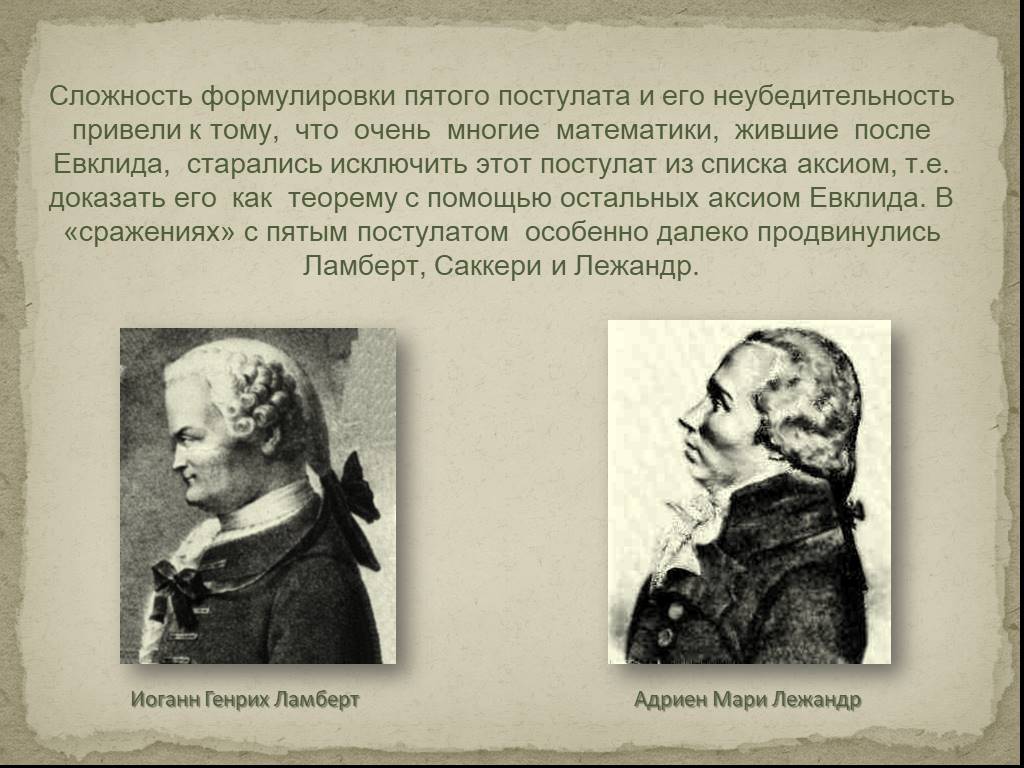
Слайды презентации
Список похожих презентаций
История геометрии
" Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать". ...История развития геометрии
ВВЕДЕНИЕ:. Геометрия возникла очень давно, это одна из самых древних наук. Геометрия (греческое, от geо — земля и metrein — измерять) - такое название ...История возникновения геометрии
В.Е. Антипина, МОУ СОШ №1 г. Красновишерска. Необходимость возникновения науки. Геометрия возникла в результате практической деятельности людей: нужно ...История возникновения Геометрии
Для первобытных людей важную роль играла форма окружавших их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для ...Зарождение и история геометрии
Мы узнаем откуда пришла, и какой раньше была геометрия. Прежде, чем идти на урок. Давайте узнаем историю геометрии и области ее применения. Геоме́трия ...Урок-семинар по геометрии на тему "Тела вращения". 11-й класс
Цели семинара. Обобщение и систематизация знаний учащихся по теме «Тела вращения». Развитие познавательных и исследовательских умений учащихся. План ...Развитие геометрии
Геометрия. Геометрия – одна из наиболее древних наук. Первые геометрические факты найдены в Вавилонских клинописных таблицах и Египетских папирусах ...Построение двумерной флаговой геометрии на основе системы аксиом Вейля
Содержание:. Эпиграф Вступление Биография Германа Вейля Система аксиом Вейля аффинной и евклидовой геометрии на плоскости Аксиоматика Вейля флаговой ...Лабораторный практикум по геометрии
Свойство равнобедренного треугольника. Сумма углов треугольника. Сумма острых углов прямоугольного треугольника. Внешний угол треугольника. Вертикальные ...История чисел. Запись чисел
Записывать числа люди научились гораздо позже, чем считать. Как вы думаете, что люди научились делать раньше: считать или записывать числа? Числа ...История треугольника
Что такое треугольник? Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства которых человек узнал еще в глубокой древности, ...История систем счисления
Десятичная система счисления. Обычная система записи чисел который мы привыкли пользоваться жизни. Десятичная система счисления встречается везде ...Вектор в геометрии
Понятие вектора. В курсе планиметрии мы познакомились с векторами на плоскости и действиями над ними. Основные понятия для векторов в пространстве ...Вводный урок геометрии
круг. МАТЕМАТИКА Алгебра Геометрия. квадрат треугольник прямая. ФИГУРЫ. ГЕОМЕТРИЯ Планиметрия Стереометрия. Изучает свойства фигур на плоскости. Изучает ...Вводное повторение курса геометрии о параллельных прямых
Назвать все углы, образовавшиеся при пересечении двух прямых третьей. 1 3 4 5 6 7 8 а в. Задача №1 2 А В Е К. Дано:. Задача № 2 С. Отрезки АВ и СЕ ...Вводное повторение курса геометрии
Задача № 1 Доказать: АС = СD. Задача № 2 В Доказать: АD = DС. Задача № 3 Доказать:. Задача № 4. Дано: АD = ЕС Доказать: DBE - равнобедренный. Задача ...Вводное повторени для 8 классов по геометрии
8 9 10 11 14 15 16 17 18 30 33 34 35 36 1 3 4 5 6 13 19 31 7. Найти: 440 D С О В А ? 2. Дано:. a0 F b0. O. N R M L. a b c 650. . 450 K E 1350 800. ...Вводное занятие по геометрии
В мире геометрии. Планиметрия Стереометрия. Сами того не зная, люди все время занимались геометрией. Издавна люди любили украшать себя, свою одежду, ...В геометрии нет царских дорог
Супертест, 1 команда. 1. 1.Как образно говорят о большом количестве чего-нибудь? А.Пруд пруди. В. Болото болтай. Б. Залив заливай. Г. Море маринуй. ...Бумажные складные модели и их использование на уроках геометрии в 10 классе
Модель 1 – «Две пересекающиеся плоскости». Согнутый пополам лист бумаги служит моделью двух пересекающихся плоскостей. Линия сгиба – прямая их пересечения. ...Конспекты
История возникновения и развития геометрии. Начальные геометрические сведения
Урок геометрии с использованием ИКТ. . Класс:. 7. Учитель:. Петрова Марина Николаевна,. учитель математики МБОУ СОШ №76. . Орджоникидзевского ...Путешествие в мир геометрии
Автор материала: Баранова Ирина Владимировна. . Место работы: МОУ «Могойтуйская средняя общеобразовательная школа №1», пгт Могойтуй, Агинского ...Применение производной в физике, алгебре и геометрии
ПЛАН-КОНСПЕКТ ЗАНЯТИЯ. . Применение производной в физике, алгебре и геометрии. . ФИО (полностью). . Сидоренко Ольга Викторовна. . ...Применение мультимедийных презентаций на уроках геометрии
Мастер-класс по теме:. «Применение мультимедийных презентаций на уроках геометрии». Пояснительная записка. Мастер-класс проходил в рамках городского ...Практикум «Решение задач по геометрии
Муниципальное общеобразовательное учреждение. средняя общеобразовательная школа № 29 поселка Мостовского. муниципального образования Мостовский ...Обобщение за курс геометрии 7 класса
Урок геометрии. 7 класс. Тема урока: Обобщение за курс геометрии 7 класса. Тип урока:. урок обобщающего повторения. Методы:. иллюстративный, ...История чисел. Запись чисел
. ПЛАН-КОНСПЕКТ. Тема: История чисел. Запись чисел. Родыгина Людмила Николаевна. . МОУ-сош №3 г.Красный Кут. . Учителя математики. . ...История чисел
Краевое государственное казённое образовательное учреждение. «Камчатская санаторная школа – интернат». Елизовского района Камчатского края. . ...История Ульяновска в числах
Технологическая карта урока. Данные об учителе: Хренкова Нина Александровна. Предмет: математика Класс: 6 ...История Нововаршавской школы в задачах на умножение дробей
Интегрированный урок по математике с элементами краеведения по теме "История Нововаршавской школы в задачах на умножение дробей", 6-й класс. . ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:6 февраля 2019
Категория:Математика
Содержит:25 слайд(ов)
Поделись с друзьями:
Скачать презентацию