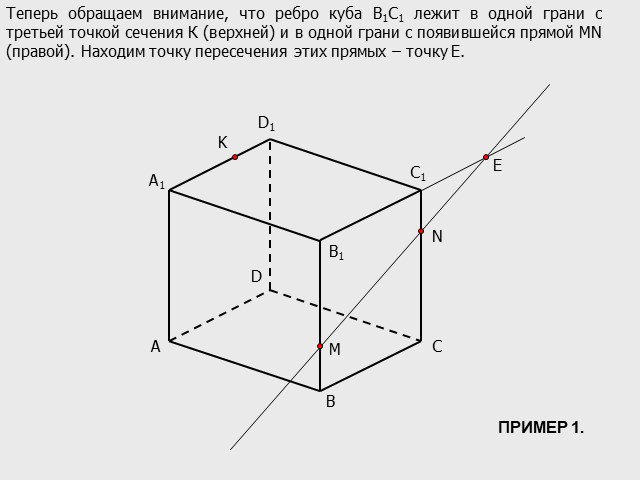
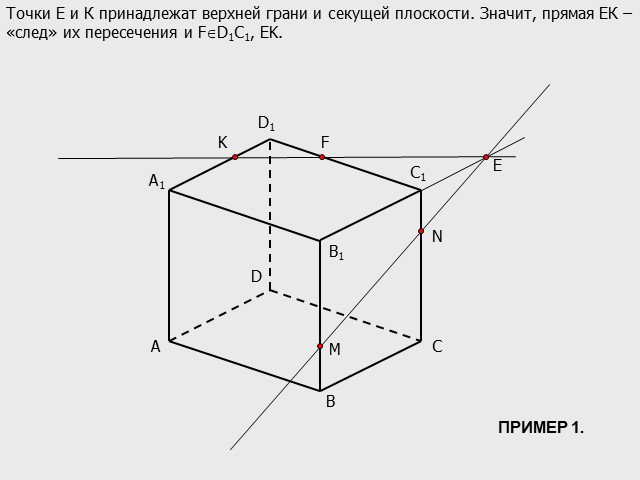
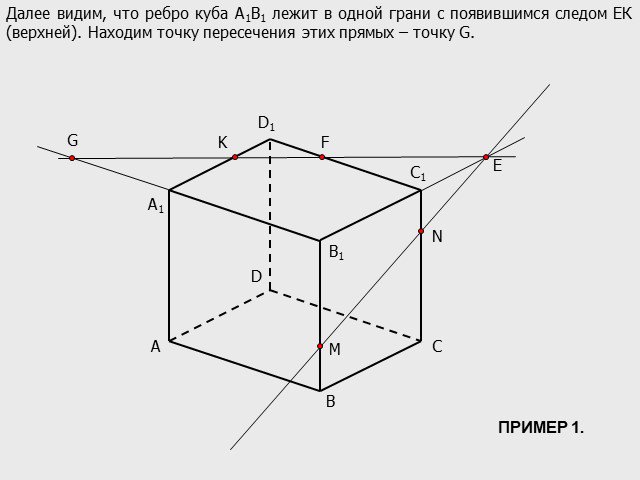
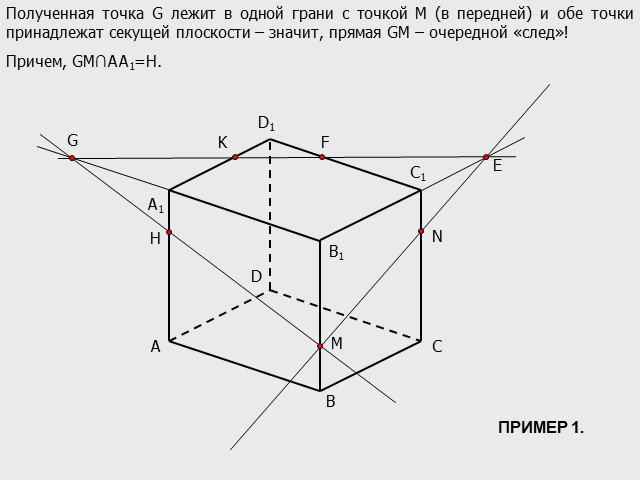
Презентация "Построение сечений многогранников методом «следа»" по математике – проект, доклад
Презентацию на тему "Построение сечений многогранников методом «следа»" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 17 слайд(ов).
Слайды презентации
Список похожих презентаций
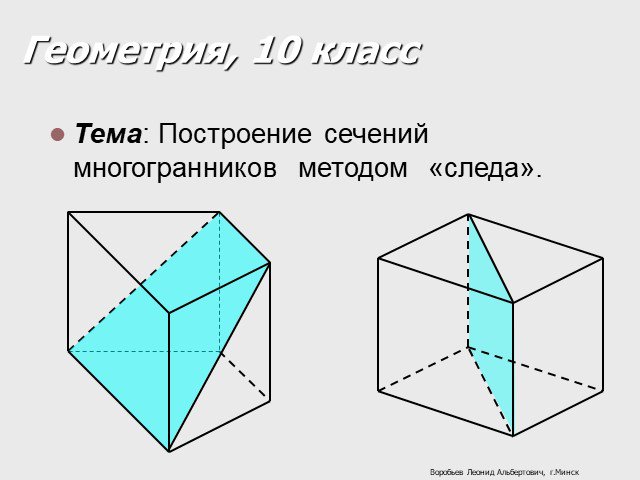
Построение сечений многогранников
Содержание. Определение. Примеры построений сечений. Задания на построение сечений. Определение. Если пересечением многогранника и плоскости является ...Построение сечений многогранников
В работе над проектом принимали участие ученики 9 класса ГОУ СОШ «Школа здоровья» №198 г. Москвы. Пономарёв Руслан Нелюбова Татьяна. Колотикова Дарина. ...Построение сечений многогранников
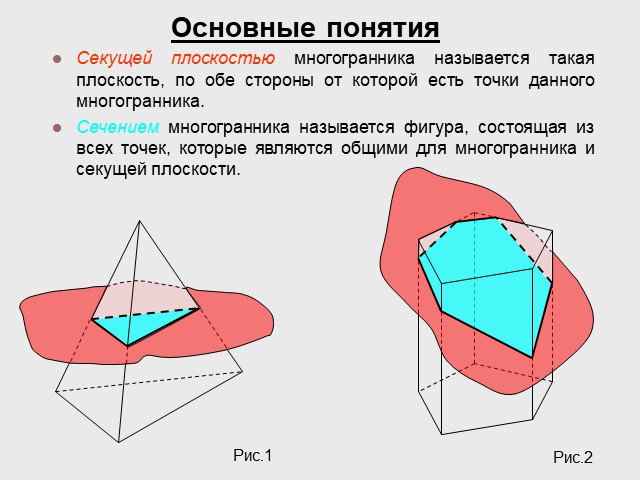
Определение сечения. Секущей плоскостью многогранника назовем любую плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая ...Построение сечений многогранников
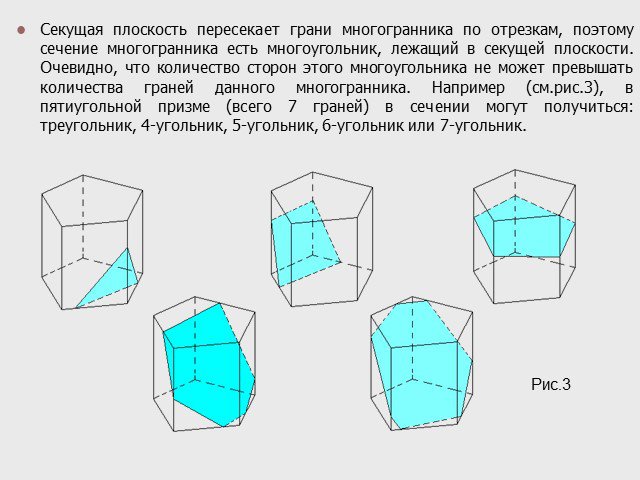
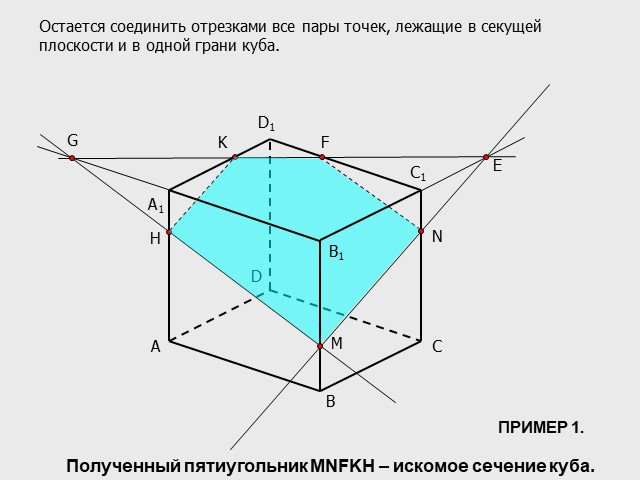
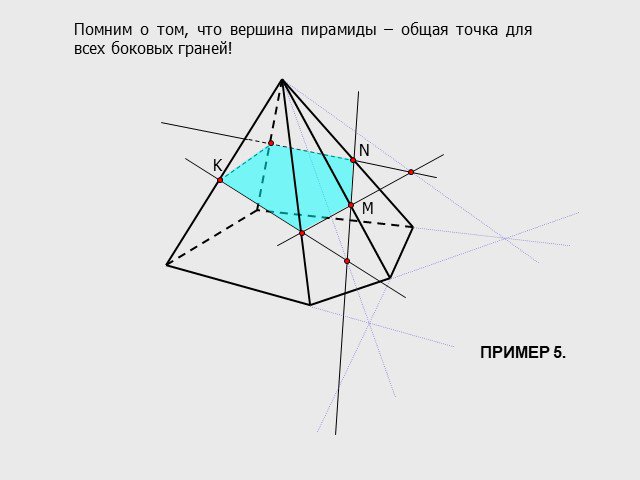
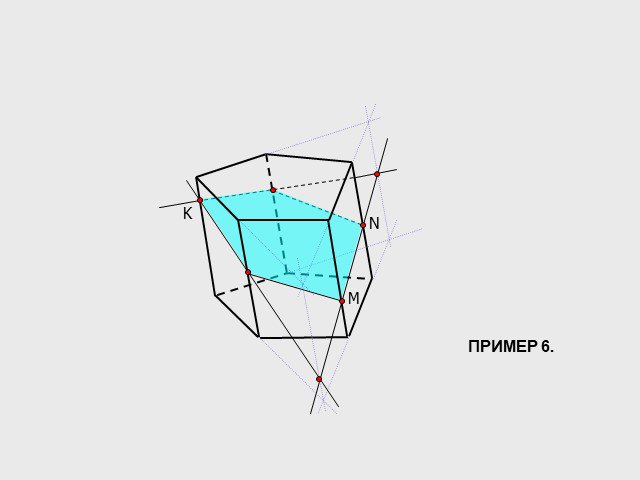
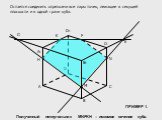
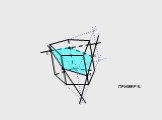
A C D A1 D1 C1 1 B B1. Многоугольник, вершины которого лежат на рёбрах многогранника, а стороны – отрезки боковых граней, называется сечением многогранника. ...Построение сечений многогранников
МНОГОГРАННИКИ. КУБ. МНОГОГРАННИКИ. ЧЕТЫРЕХУГОЛЬНАЯ ПИРАМИДА.C. МНОГОГРАННИКИ. ТЕТРАЭДР. МНОГОГРАННИКИ. ТРЕУГОЛЬНАЯ ПРИЗМА. МНОГОГРАННИКИ. ОТВЕТЬТЕ ...
Построение сечений многогранников геометрия
Обучающая цель: формирование умений и навыков построения сечений. Развивающая цель: формирование и развитие у учащихся пространственного представления. ...Построение сечений многогранников
Задачи урока:. Повторим геометрические понятия и утверждения. Отработаем умения построения сечений. Решим проблемные задачи. Сформулируем инструкцию ...Решение задач на построение сечений многогранников
№69. N M P R. Найдите периметр сечения, если SВ=8 см, АС=6 см. №70. К М. №71. Р. №78. №79(а). А С В D. №79(б). №81. в) построить сечение через точки ...Задачи на построение сечений куба
1. Актуализация. 2. Изучение нового материала. 3. Домашнее задание. 4. Подведение итогов. Дайте определение многограннику. Назовите следующие фигуры:. ...Задачи на построение сечений
Сечение Может быть построено по трем точкам, не лежащим на одной прямой, а также если заданы точка и прямая, причем точка не лежит на прямой. Рассмотрим ...Решение сложных геометрических задач на построение методом спрямления
Задача №1. «Построить равнобедренный треугольник по его периметру P и высоте h». P h. Анализ B C O A С1 A1. Построение C1. Доказательство α. Исследование. ...Моделирование в стереометрии Построение сечений
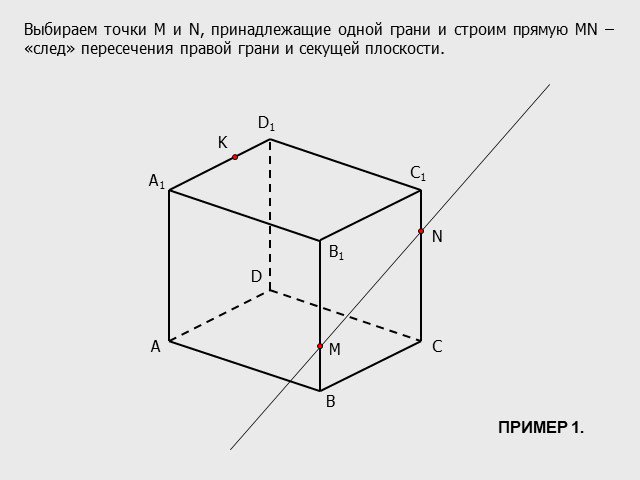
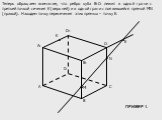
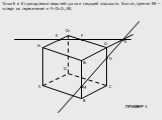
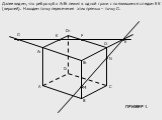
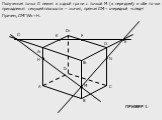
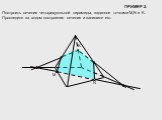
Теорема:. Если две непараллельные прямые, принадлежащие одной плоскости, пересекают прямую, не лежащую в этой плоскости, то все три прямые пересекаются ...Построение сечений: метод следа
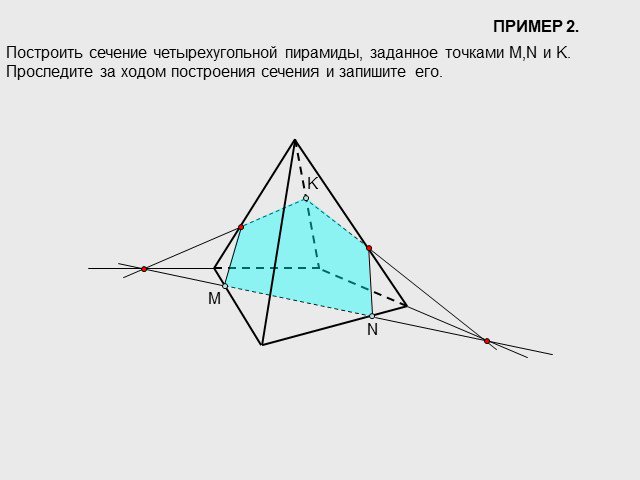
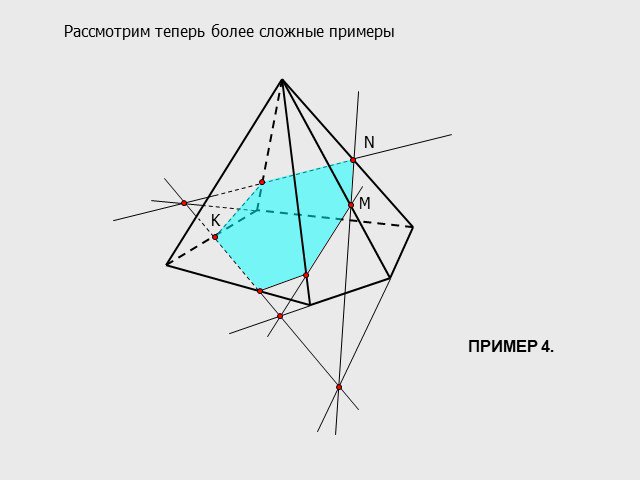
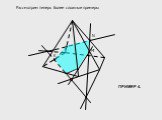
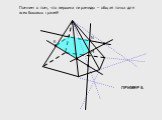
Существует три основных метода построения сечений многогранников: Метод следов. Метод вспомогательных сечений. Комбинированный метод. Метод следов ...Решение задач на построение сечений тетраэдра
Тестирование по теме «Тетраэдр».Запишите правильные ответы в тетрадь. Поменяйтесь тетрадями и проверьте правильность ответов. C B C A C A B A B ...
Построение сечений
Цели, объект и предмет исследования. Цель — обобщение сведений по теме «сечения» и построение 3D моделей сечений многогранников. Объект исследования ...Построение сечений параллепипеда
Цели урока. Определить виды сечений параллелепипеда Установить взаимосвязь между видом сечения и расположением точек на ребрах параллелепипеда Научиться ...Пирамида. Построение пирамиды и её плоских сечений. Усечённая пирамида. Правильная пирамида.
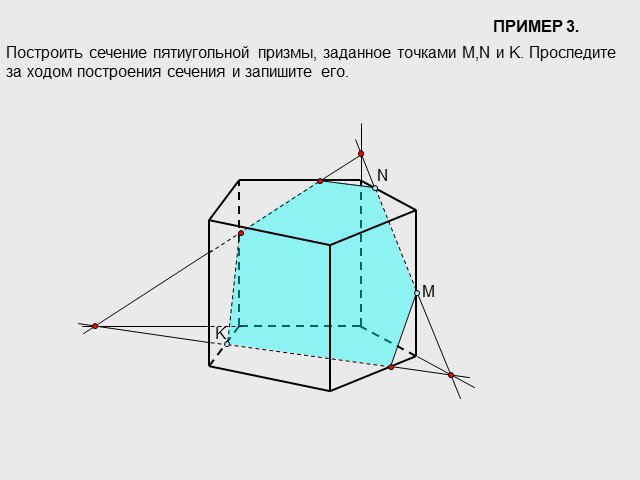
Что такое пирамида? Пирамида – это многогранник, у которого одна грань ( основание пирамиды ) – это произвольный многоугольник ( ABCDE, рис.), а остальные ...Призма. Построение сечений призмы плоскостями
План урока. Тема: Призма. Построение сечений призмы плоскостями. Цель: Дать определение призмы. Научить строить сечения призмы плоскостями. Оборудование: ...Построение сечений многогранника
Содержание. Определение. Примеры построений сечений. Задания на построение сечений. Определение. Если пересечением многогранника и плоскости является ...Построение графика функции методом ее исследования с помощью производной
доцент кафедры математического образования Батан Любовь Федоровна. учитель математики первой квалификационной категории МОУ лицей № 176 Ткаченко Зоя ...Конспекты
Построение сечений многогранников
Муниципальное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа № 1 им. Гриши Акулова. . г.Донецка, Ростовской области. ...Построение сечений многогранников на основе аксиоматики
Чудаева Елена Владимировна, учитель математики,. МОУ «Инсарская средняя общеобразовательная школа №1»,. г. Инсар, Республика Мордовия. . Автор. ...Построение сечений многогранников
Государственное бюджетное образовательное учреждение. Лицей №281. «Построение сечений многогранников». Урок геометрии. 10 класс. ...Построение сечений многогранников. Параллельность прямых и плоскостей в пространстве
Построение сечений многогранников. Параллельность прямых и плоскостей в пространстве. Тип урока:. повторительно-обобщающий. Цели и задачи урока:. ...Построение сечений многогранника
Матлашевская Лилия Петровна. Учитель математики. . МАОУ «Гимназия № 2» г.Перми. Построение сечений многогранника. Цели и задачи урока:. Закрепление ...Построение сечений
Шарова Елена Владимировна. Учитель математики. Муниципального общеобразовательного учреждения Усвятская средняя общеобразовательная школа. Номинация: ...Решение уравнений методом подстановки
Открытый урок по теме:. . . Решение уравнений методом подстановки. . . Учитель математики ГОУ гимназии № 1549 Шмелева Ирина Дмитриевна. ...Уравнение. Решение уравнений методом подбора
Конспект урока математики. 2 класс. Тема:. «Уравнение. Решение уравнений методом подбора». Цель:. Формирование. . представления об уравнении ...Решение неравенств методом интервалов
ПЛАН-КОНСПЕКТ УРОКА Решение неравенств методом интервалов. . ФИО: Метельская Т.А. . . . . Место работы : МОУ Лицей №7 г. Саяногорска. ...Решение неравенств методом интервалов
Тема урока «Решение неравенств методом интервалов». Цель урока. : формировать навыки и умения учащихся при решение неравенств методом интервалов; ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Математика
Автор презентации:Воробьев Леонид Альбертович
Содержит:17 слайд(ов)
Поделись с друзьями:
Скачать презентацию