Конспект урока «Построение сечений многогранников» по геометрии для 10 класса

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа № 1 им. Гриши Акулова

г.Донецка, Ростовской области

Конспект урока по геометрии в 10 классе

«Построение сечений многогранников»

подготовил

учитель математики

Кущий Надежда Васильевна

2011

Тип урока: Урок-практикум

Цели урока:

1. Развитие пространственного воображения обучаемых, их логического мышления и индуктивного анализа.

2. Формирования навыков решения задач на построение сечений многогранников.

3. Обучение умению анализировать свои действия для достижения поставленной цели, поиску оптимального пути ее выполнения, самоконтролю.

Оборудование: ПК, проектор, Microsoft PowerPoint, презентация «Построение сечений многогранников», раздаточный материал в виде готовых чертежей с задачами, тела многогранников.

Ход урока:

1. Сообщение темы и цели урока.

2. Проверка опорных знаний и умений обучаемых. (Сл. 4-7)

3. Решение задач с объяснением хода решения учителем. (Сл. 8, 10, 11)

4. Применение пространственного моделирования для решения задач. (Сл. 9, 12, 13, 14)

5. Подведение итогов.

6. Домашнее задание. (Сл. 15)

Сообщение темы и цели урока

Проверка опорных знаний и умений

Вопросы к классу:

- Что значит построить сечение многогранника плоскостью?

- Как могут располагаться относительно друг друга многогранник и плоскость?

- Как задается плоскость?

- Когда задача на построение сечения многогранника плоскостью считается решенной?

Правила построения сечений многогранников:

1) проводим прямые через точки, лежащие в одной плоскости;

2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого

а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);

б) параллельные грани плоскость сечения пересекает по параллельным прямым.

Построение простейших сечений многогранников. Слайды 4 -7, задание 1 - 4.

Решение задач с объяснением хода решения учителем. (Сл. 8, 10, 11)

Применение пространственного моделирования для решения задач. (Сл. 9, 12, 13, 14)

Данные этапы урока посвящены непосредственному решению задач. Часть задач решается и комментируется учителем. Навыки построения сечений закрепляются обучаемыми самостоятельно с последующей проверкой и комментированием.

Метод следов заключается в построении следов секущей плоскости на плоскость каждой грани многогранника. Построение сечения многогранника методом следов обычно начинают с построения, так называемого, основного следа секущей плоскости, т.е. следа секущей плоскости на плоскости основания многогранника.

Задача №5. Построить сечение четырехугольной пирамиды, проходящее через M, N, K. (Слайд 8)

К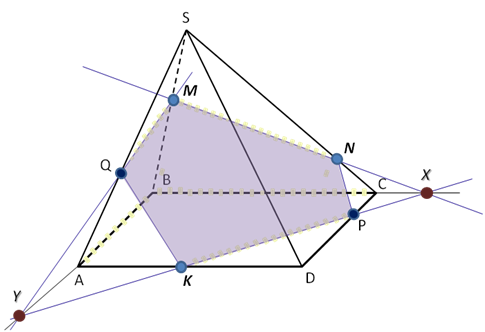раткая запись решения

1. M↔N

2. MN ∩ BC = X

3. X ↔ K

4. XK ∩ DC = P

5. N ↔ P

6. XK ∩ BA = Y

7. Y ↔ M

8. YM ∩ AS = Q

MNPKQ – искомое сечение

Задача №6. Построить сечение призмы, проходящее через точки:

K – принадлежит ребру АА₁

L – принадлежит грани АА₁В₁В

M – принадлежит грани АВС (Слайд 9)

К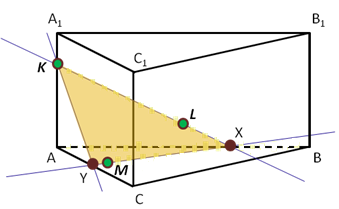раткая запись решения

1. K ↔ L

2. KL ∩ AB = X

3. X ↔ M

4. XM ∩ AC = P

5. Y ↔ K

KXY – искомое сечение

Задача 7. Построить сечение параллелепипеда, проходящее через точки H, I, F:

а) используя свойство параллельных плоскостей, пересеченных третьей (Слайд 10)

б) используя метод следов (Слайд 11)

a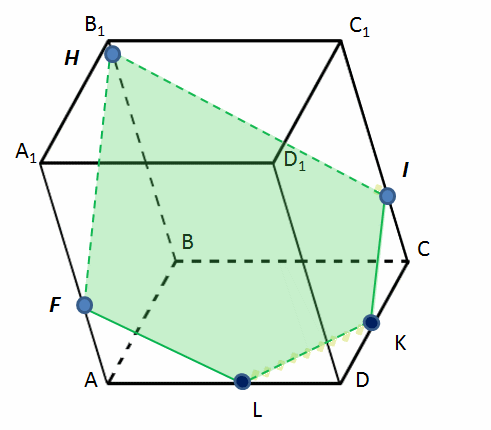) Краткая запись решения

1. H ↔ I

2. H ↔ F

3. FL || HI

4. FL ∩ AD = L

5. IK || HF

6. IK ∩ DC = K

7. L ↔ K

HIKLF – искомое сечение

б)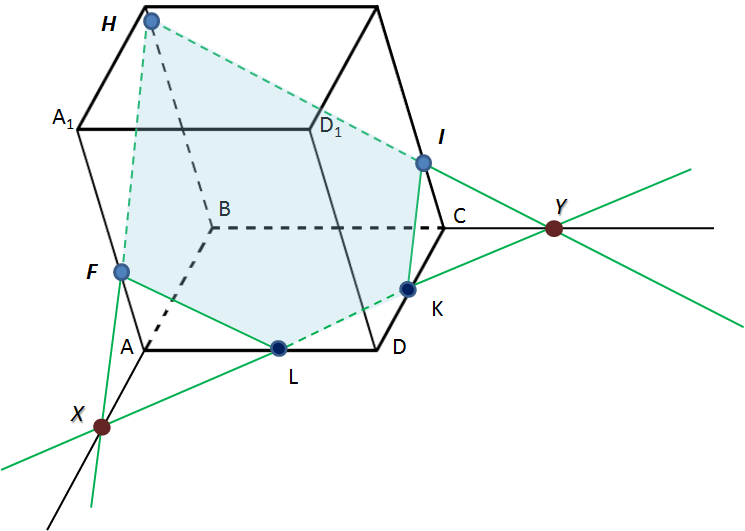

Краткая запись решения

1. H ↔ F

2. H ↔ I

3. HF ∩ BA = X

4. HI ∩ BC =Y

5. XY ∩ AD = L

6. XY ∩ CD = K

7. F ↔ L

8. I ↔ K

HIKLF – искомое сечение

Задача 8. Построить сечение призмы, проходящее через точки H, K, R. (Слайд 12)

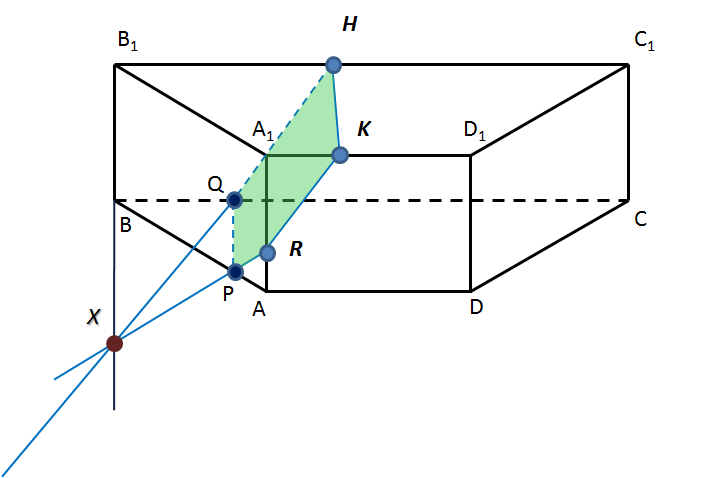
Краткая запись решения

1. H ↔ K

2. K ↔ R

3. HQ || KR

4. HQ ∩ B₁B =X

5. X ↔ R

6. XR ∩ AB =P

7. P ↔ Q

HKRPQ – искомое сечение

Задача 9. Построить сечение параллелепипеда, проходящее через точки M, N, K:

а) используя свойство параллельных плоскостей, пересеченных третьей (Слайд 13)

б) используя метод следов (Слайд 14)

a)

К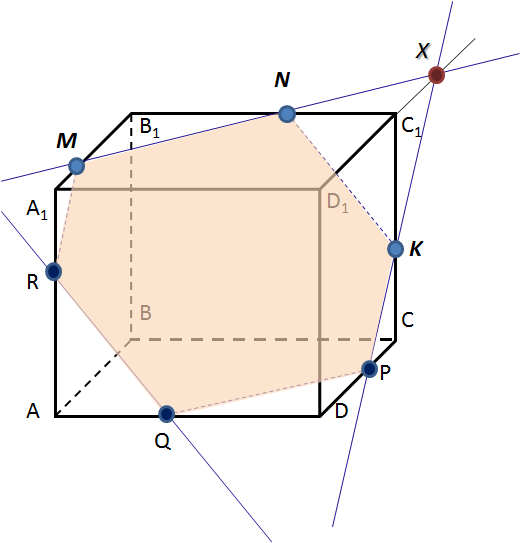раткая запись решения

1. M ↔ N

2. N ↔ K

3. MN ∩ D₁C₁ = X

4. XK ∩ DC = P

5. PQ || NM

6. QP || KN

7. R ↔ M

MNKPQR – искомое сечение

б)

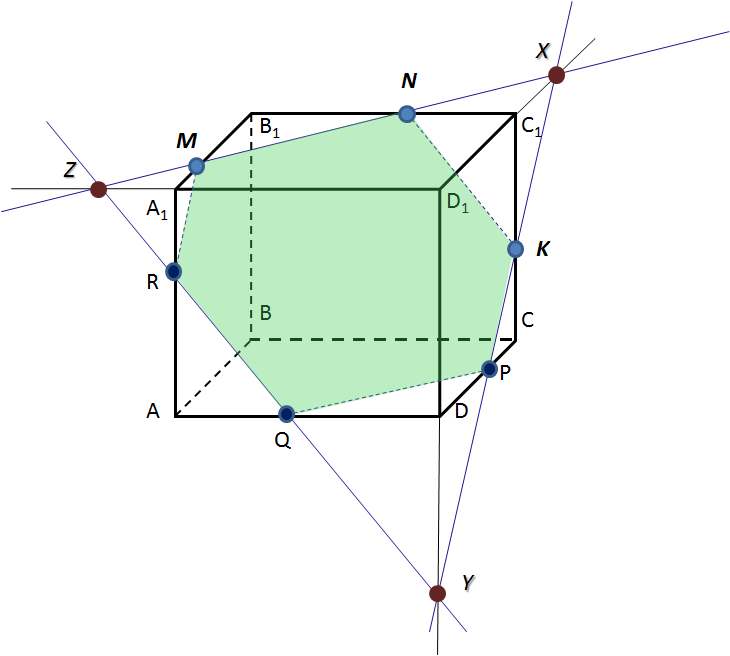
Краткая запись решения

1. M ↔ N

2. MN ∩ D₁C₁ = X

3. X ↔ K

4. XK ∩ DC = P

5. N ↔ K

6. D₁D ∩ XK = Y

7. A₁D₁ ∩ MN = Z

8. Z ↔ Y

9. ZY ∩ A₁A = R

10. ZY ∩ AD = Q

11. M ↔ R

12. Q ↔ P

MNKPQR – искомое сечение

Домашнее задание

Уровень А

Учебник §4, п. 14; № 71, 80.

Уровень В (Слайд 15)

Построить сечение тетраэдра, проходящее через точки:

Q – принадлежит грани ABC;

R – принадлежит ребру AB;

S – принадлежит ребру DB.

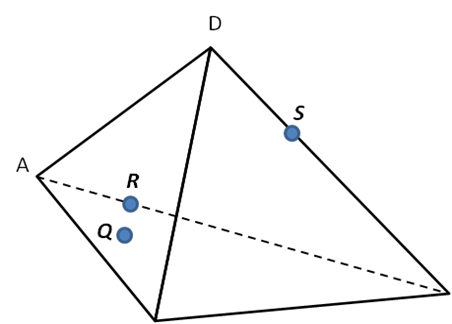
Уровень С

Придумать и решить задачу на построение сечения прямоугольного параллелепипеда плоскостью, проходящей через 3 произвольно выбранные точки на ребрах и/или гранях.

Подготовить карточку с данной задачей.

Подведение итогов

В ходе урока были сформированы навыки решения задач на построение сечений многогранников.

Использованные материалы и ресурсы

1. Атанасян Л.С., и др. Геометрия 10-11. – М.: Просвещение, 2008.

2. Литвиненко В.Н., Многогранники. Задачи и решения. – М.: Вита-Пресс, 1995.

3. Смирнов В.А., Смирнова И. М., ЕГЭ 100 баллов. Геометрия. Сечение многогранников. – М.: Экзамен, 2011.

4. Учебно-методическое приложение к газете «Первое сентября» «Математика». Федотова О., Кабакова Т. Интегрированный урок "Построение сечений призмы", 9/2010.

5. http://www.cartoonclipartfree.com/Cliparts_Free/Schule_Free/Cartoon_Clipart_Free_Page_1.html