Конспект урока «Площади плоских фигур. Пространственные тела. Площади поверхности многогранников» по геометрии



















 Приложения 1
Приложения 1
Разработки уроков с профессиональной направленностью
Урок 1
Тема урока:
Площади плоских фигур. Пространственные тела. Площади поверхности многогранников.
Тип учебного занятия:
Урок обобщения и систематизации.
Цели урока:
-
Организовать деятельность учащихся по обобщению и систематизации знаний
-
Выявить типичные ошибки и проблемы в знаниях учащихся с целью их последовательного устранения
-
Создавать условия для развития у учащихся умения анализировать, применять знания при решении задач с практическим содержанием, умение осуществлять самоконтроль
-
Помочь учащимся осознать практическую значимость данных понятий
Форма учебного занятия:
Комбинированный урок
Оснащение урока:
-
Справочные материалы;
-
Модели пространственных тел и их развертки
Ход урока:
I. Организация занятия
1) Проверка готовности класса к уроку
2) Знакомство с темой, целями и задачами урока.
II. Повторение ранее изученного материала
1) Повторение понятия площади, площади плоских фигур и формул для их вычисления проходит с помощью демонстрационных таблиц и справочных таблиц, находящихся на столах учащихся.
Вопросы учащимся:
-
Какие плоские фигуры вы знаете, почему они называются плоскими?
-
Что значит найти площадь фигуры?
-
Какие измерения необходимы, чтобы найти площадь
Прямоугольника
Параллелограмма
Треугольника
Трапеции
Правильного многоугольника
(треугольника, многоугольника)?
2) Решение тренировочных упражнений на применение формул площади плоских фигур.
По количеству верно решенных заданий учащиеся выставляют себе предварительную оценку.
-
понятие «Пространственное тело», площадь поверхности пространственных тел осуществляется по таблице «Пространственные тела». Для повторения используются модели многогранников и их развертки.
Ключевые вопросы:
-
чем пространственное тело отличается от плоской фигуры?
-
Какие вы знаете пространственные тела?
-
Что является поверхностью пространственного тела и из каких фигур она состоит?
-
Задание учащимися:
-По предложенным моделям определить:
-
параллелепипед, прямоугольный параллелепипед,
-
призму, пирамиду, усеченную пирамиду.
-Вспомните определения и свойства данных тел.
-Запишите формулы для вычисления площади их поверхности. (Работа проводится с комментированием учащихся)
Наиболее подготовленные учащиеся получают задание: «Вычислите площадь поверхности пространственного тела (по выбору)»,
III. Применение знаний данной темы при решении задач.
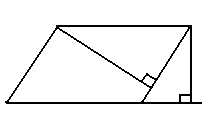
Решите задачу: Сколько квадратных метров материала пошло на изготовление чехла сиденья в кабине автомобиля, (размеры на рисунке)
130
1250
D С
180
A B
480
Учащийся проводит анализ задачи:
-
Сидение – прямая четырехугольная призма, в основании – трапеция
S пов. призмы = 2Sосн +Sбок; Sбок = Pосн*H
2) так. одна боковая грань не обшивается, то
Sбок=(AD+DC+CB)*H
3) Чтобы найти длину стороны DC применяем теорему Пифагора для
∆ MCD – прямоугольный: DC =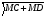
Решение учащиеся выполняют самостоятельно.
IV. Подведение итогов.
Общая характеристика работы класса, оценки учащихся, работающих самостоятельно, сравнение с их самооценкой.
Рекомендации учащимся по преодолению вскрытых недостатков.
V. Домашнее задание.
-
повторить формулы площади фигур
-
составить и решить задачу с практическим содержанием на вычисление площади поверхности
-
индивидуальные задания: выполнить соответствующие измерения и найти площадь поверхности металлического гаража
-
темы проектов по теме: «Объем и площадь поверхности пространственного тела». Сообщение учащегося по историческому блоку.
VI. Рефлексия.
Оценки урока, самооценка учащихся, выводы и предложения учащихся по вопросам дальнейшего сознательного изучения темы.
Общая оценка урока учащимися.
Учащиеся ставят «+» в какой-то отдел листа рефлексии
| Не совсем понял | Ничего не понял | И не хочу понимать! |
Справочный материал
Свойства и формулы площади плоских фигур:
1) прямоугольник
а С Д
АД=ВС; АД II BC
L А=L В=L Д=98
в 0
в
а В А
Площадь:
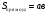
(площадь прямоугольника равна произведению сторон: длинны и высоты)
2) Ромб
М
В
а
а
А
С
Д
а
а
л
АС┴ДВ (диагонали ромба взаимно перпендикулярны
и делятся точкой пересечения М пополам)
АМ=МС; ДМ=МВ
АД=ДС=ВС=АВ=а
Площадь:
S=а2sin л (л-угол между сторонами).  (d1 и d2- диагонали ромба)
(d1 и d2- диагонали ромба)
3) квадрат
АС=ДВ=d- диагональ
d=а √2
а А С Д
а
а
а
4) параллелограмм
h а
a
в
л
Площадь: S=aв sin л, S=ah
Справочные и тренировочные упражнения: ( III)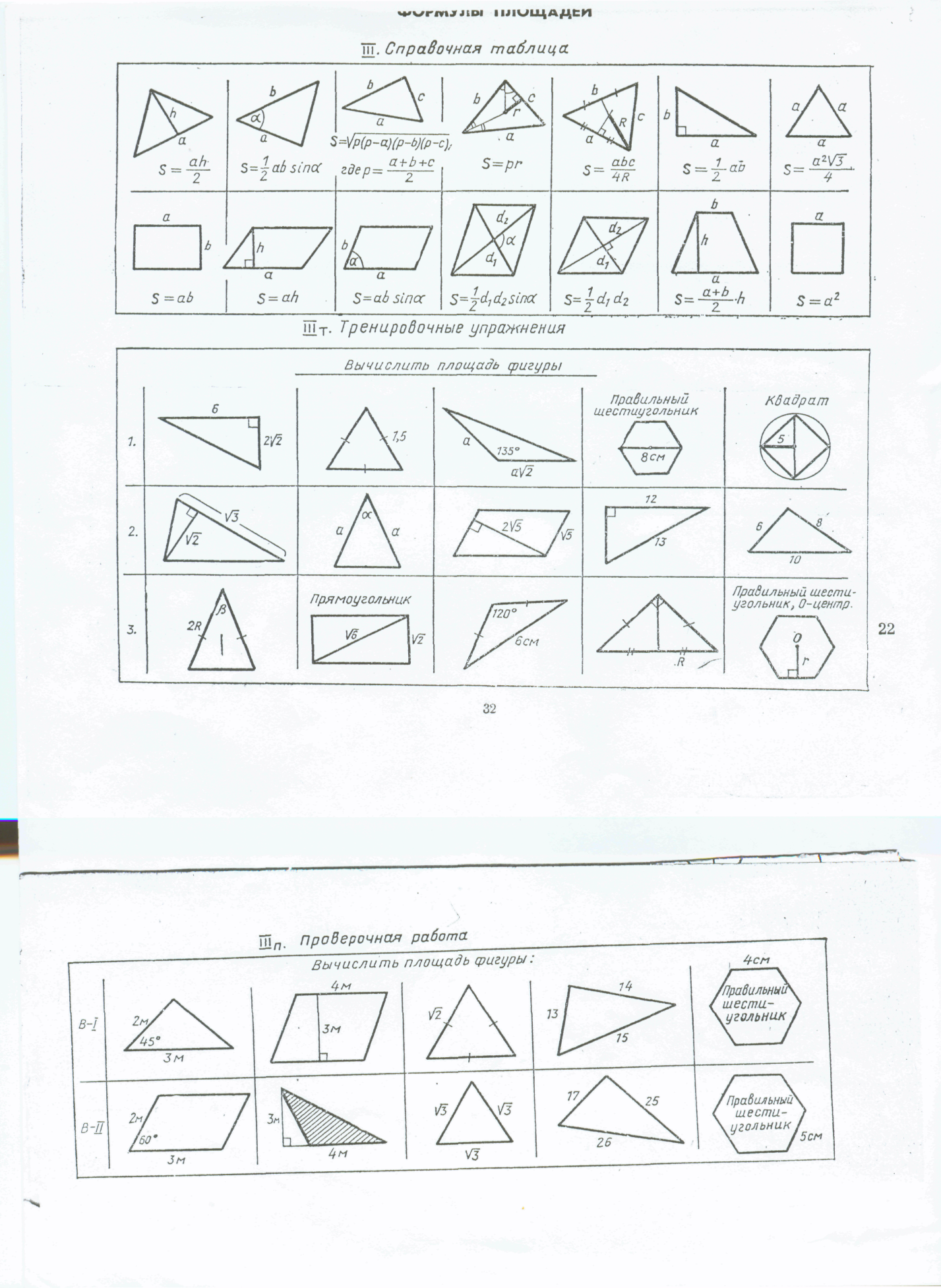
Здесь представлен конспект к уроку на тему «Площади плоских фигур. Пространственные тела. Площади поверхности многогранников», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Геометрия Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

