Конспект урока «Площади фигур» по геометрии для 8 класса

Конспект урока для 8 класса по геометрии "Площади фигур"

Цели урока: повторить пройденный материал, вывести формулу нахождения площади прямоугольного треугольника, ромба, любого треугольника; ознакомить со свойствами площади треугольника. Сформулировать и доказывать теорему о площадях треугольников с равными углами.

Воспитание аккуратности;

воспитание творческого подхода к решению задач.

Развитие самостоятельности, интереса к математике.

Ход урока. I. Организационный момент.

II. Актуализация знаний.

1. Устные упражнения для повторения.

ВЕРНО ЛИ, что:

Задача 1.Дан прямоугольник со сторонами 8 и 3.

Верно ли, что: S = 2 ( а + в ) =2 ( 8 + 3 ) =2 ∙11= 22.

Ответ: нет, S = a b = 8 ∙ 3 = 24.

Задача 2. Дан параллелограмм.

a = 12, h_a = 3, b = 4, h_b = 9.

Верно ли, что: S = a b =12∙ 4 = 48?

Ответ: нет, S = a h = 12 ∙ 3 = 36.

Задача 3. Дан квадрат. S = 10.

Верно ли, что: а =5?

Ответ: нет, а = √10.

2. Знаете ли вы свойства площадей:

Задача 1. (рис.1) S пр. = Q , CO = OD. S _ABE = ?

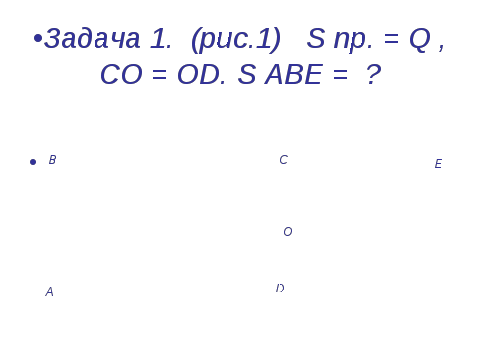
Задача 2. (рис.2) S _ABCD = S , OA = OK. S _AKD = ?

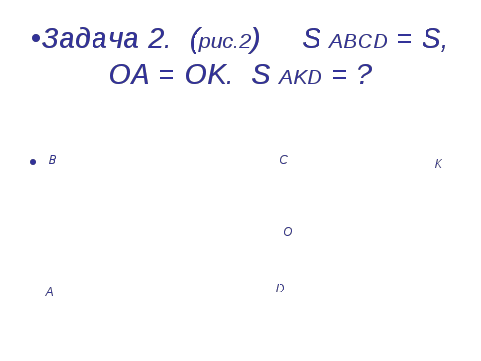
3. Основная часть.

Рассмотрим задачу: Дан прямоугольник со сторонами а и b (рис 3). Найти площадь прямоугольного треугольного треугольника АВD.

Решение: (обучающиеся)

ВЫВОД: площадь прямоугольного треугольного равна половине произведения его катетов.

Устно (рис.4,5)

Задача о ромбе 1: диагонали ромба равны 6 и 8.

Найти его площадь (рис 6).

Задача о ромбе 2: диагонали ромба равны d1 u d2/

Найти его площадь (рис 7).

ВЫВОД: площадь ромба равна половине произведения его диагоналей. S =

Вернемся к треугольникам. А если рассмотреть не прямоугольный, а любой произвольный треугольник? Как найти его площадь?

Решают ученики.

Вывод: S =

(рис.8,9)

Примеры: (рис10)

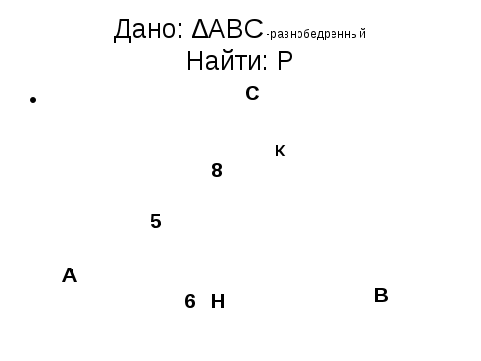
Задача. В равнобедренном треугольнике основание равно 6, высота, опущенная к основанию, равна 8, а высота,. проведенная к боковой стороне, равна 5. Найти Р. (рис11)

3. Закрепление. Задачи.

Свойство 1. Если вершину треугольника двигать по прямой, параллельно основанию, то площади полученных треугольников равны (рис 12)

Свойство 2. Медиана треугольника делит его на два равновеликих

треугольника.

Задача. Пусть площадь треугольника АВС равна S.

Если основание треугольника разделить на 3

равные части и провести отрезки CD , CE, то

площадь треугольника ADC равна?

S _ADC = 1/3 S _ABC.

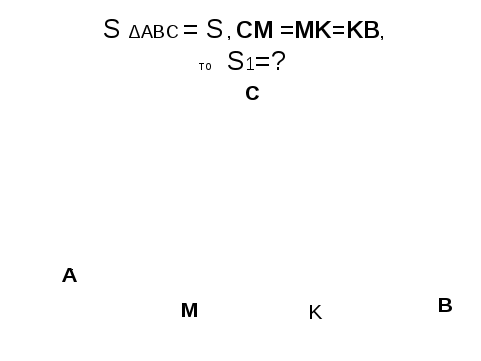
Как относится площадь треугольника AKC к площади треугольника ABC?

S _FEC = 2/3 S _ABC .

Дополнительная задача. Сторону параллелограмма разделили на 4 равные части (рис13). Найти площадь треугольника АВЕ, если площадь параллелограмма равна S.

Свойство 3. Рассмотрим два треугольника с

одинаковыми высотами, равными h

НАЙТИ отношение S1 к S2.

Решение: = =

Вывод:

Если высоты треугольников равны, то их площади относятся как основания.

ТЕОРЕМА: Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведение сторон, заключающих эти равные стороны.

Доказательство.

Задача для закрепления теоремы (рис 14).

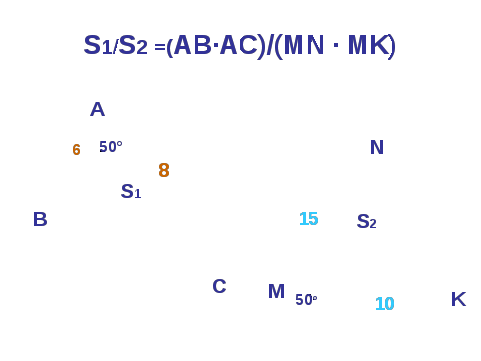
3. Графический диктант.

1. S квадрата = a²

2. F₁ = F₂ ,то S ₁ = S₂

3. Sромба= 4 a

4. a = 1,5 , то S квадрата = 6

5. a = 6, b = 5 ,то S = 30 ( прямоугольного треугольника)

6. S ромба = d₁ d₂ /4

7. 1 кв.м.= 10000 кв.см

8. Sпрям. = 2ab

Ответы: ++ - - - -+ -

3. Заключение.

Значит, сегодня вы узнали, как вычислить площадь прямоугольного треугольника, площадь ромба, площадь любого треугольника. А также рассмотрели свойства площадей треугольников.

Повторение по слайдам.

Оценивание.

Список использованной литературы:

1. Геометрия. Учебник для 7-9 классов общеобразовательных учреждений. Авторы: Л.С. Атанасян и др.

2. Ресурсы Интернета: www. images.yandex.ru, ru.wikipedia.org.

3. Начальные геометрические сведения. 7-й класс. Швиммер Галина Евгеньевна. Преподавание математики, Конкурс «Презентация к уроку»

4. http://ru.wikipedia.org/wiki/Геометрия - свободная энциклопедия.

5. http://www.krugosvet.ru/enc/nauka_i_tehnika/matematika/GEOMETRIYA.html