Конспект урока «Построение сечений многогранников. Параллельность прямых и плоскостей в пространстве» по математике

Построение сечений многогранников.

Параллельность прямых и плоскостей в пространстве

Тип урока: повторительно-обобщающий.

Цели и задачи урока:

• повторение и обобщение знаний, умений и навыков по построению сечений многогранников;

• развитие устной речи учащихся, абстрактно-логического мышления, пространственного воображения;

• воспитание умения слушать других людей, организованности, ответственности за свой труд и труд одноклассников.

Оборудование: компьютер, проектор, экран, карточки с заданиями.

Ход урока

1. Организационный момент.

Сообщение учащимся целей и плана урока.

2. Теоретический опрос

А) фронтальный:

Вопросы:

1. Какой многогранник называется правильным?

2. Что такое тетраэдр?

3. Дайте понятие секущей плоскости.

4. Что такое сечение?

5. Как построить сечение многогранника плоскостью?

6. Какие прямые называются параллельными?

7. Какие прямые называются скрещивающимися?

8. Признак параллельности прямых. (две прямые параллельны третьей)

9. Какие прямая и плоскость называются параллельными?

10. Признак параллельности прямой и плоскости.

11. Какие плоскости называются параллельными?

12. Свойство параллельных плоскостей, используемое при построении сечений.

13. Признак параллельности плоскостей.

Б) тест по теоретическому материалу

Тест

1. Если две плоскости имеют общую точку, то

а) они называются пересекающимися

б) они пересекаются по прямой, проходящей через эту точку

в) они параллельны

2. Через прямую и не лежащую на ней точку

а) проходит плоскость, и притом только одна

б) проходит бесконечное количество плоскостей

в) нельзя провести плоскость

3. Если прямая пересекает две параллельные прямые, то

а) она пересекает плоскость, образованную этими прямыми

б) она параллельна плоскости, образованной этими прямыми

в) она лежит в плоскости, определяемой этими параллельными прямыми

4. Две прямые называются скрещивающимися, если

а) они лежат в одной плоскости и не пересекаются

б) если они не пересекаются

в) если они не пересекаются и не параллельны

5. Если две прямые параллельны третьей прямой, то

а) они параллельны

б) они лежат в одной плоскости

в) они скрещивающиеся

1 – Б, 2 – А, 3 – В, 4 – В, 5 – А.

3. Самостоятельная работа.

Учащиеся выполняют построение сечений многогранников. Затем правильное решение высвечивается на экране с помощью проектора. Ученики самостоятельно проверяют правильность своего построения. Количество верных ответов заносится в таблицу достижений учащихся.

Задания для самостоятельной работы

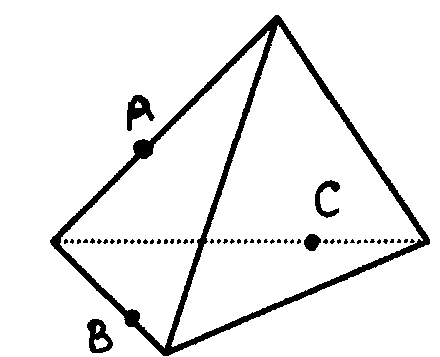
1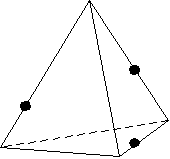. Постройте сечение тетраэдра плоскостью, проходящей через точки А, В, и С.

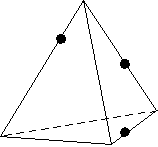
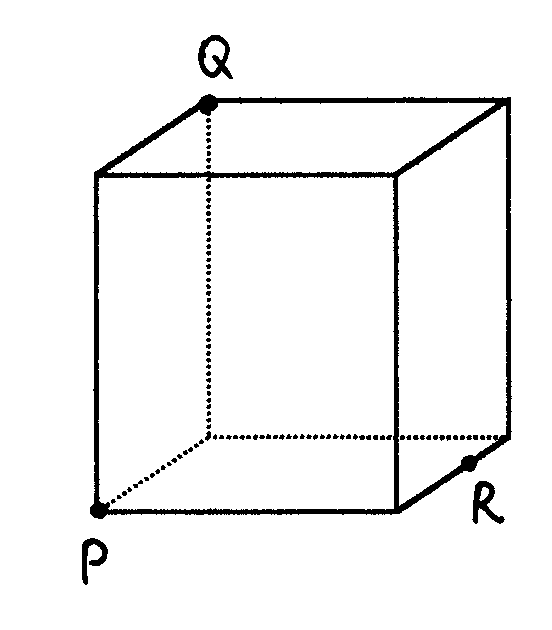
2. Постройте сечение прямоугольного

параллелепипеда плоскостью, проходящей

через отмеченные точки

4. Индивидуальная работа

Каждый ученик получает индивидуальную задачу. Трое решают свою задачу на доске. Остальным в это время предлагается рассказать, как решалась задача по готовому чертежу, который высвечивается на экране с помощью проектора.

З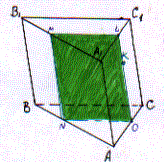адачи для самостоятельного решения у доски.

1. Точка K взята в грани ACC₁A₁ треугольной призмы АВСА₁В₁С₁. Постройте сечение призмы плоскостью, проходящей через точку K параллельно плоскости BCC1.

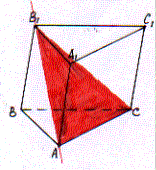
2. Постройте сечение призмы ABCA1B1C1 плоскостью, проходящей через прямую AB1

параллельно прямой A1C1.

3. На ребрах AD, CD и MD пирамиды MABCD взяты соответственно точки P, Q и D₁. Постройте линию пересечения плоскостей MDB и D₁PQ.

4. АВСА₁С₁– треугольная призма, точка F – середина ребра АВ, точка О лежит на продолжении ребра ВС так, что С расположена между В и О. Постройте сечение призмы плоскостью В₁FO.

После ответа каждого ученика идет совместное обсуждение оценок, результат которого записывается в таблицу достижений учащихся. Обсуждается так же грамотность речи, отмечаются наиболее удачные ответы

5. Подведение итогов.

Подсчитывается общее количество набранных баллов, выставляются отметки в журнал.

6. Домашнее задание