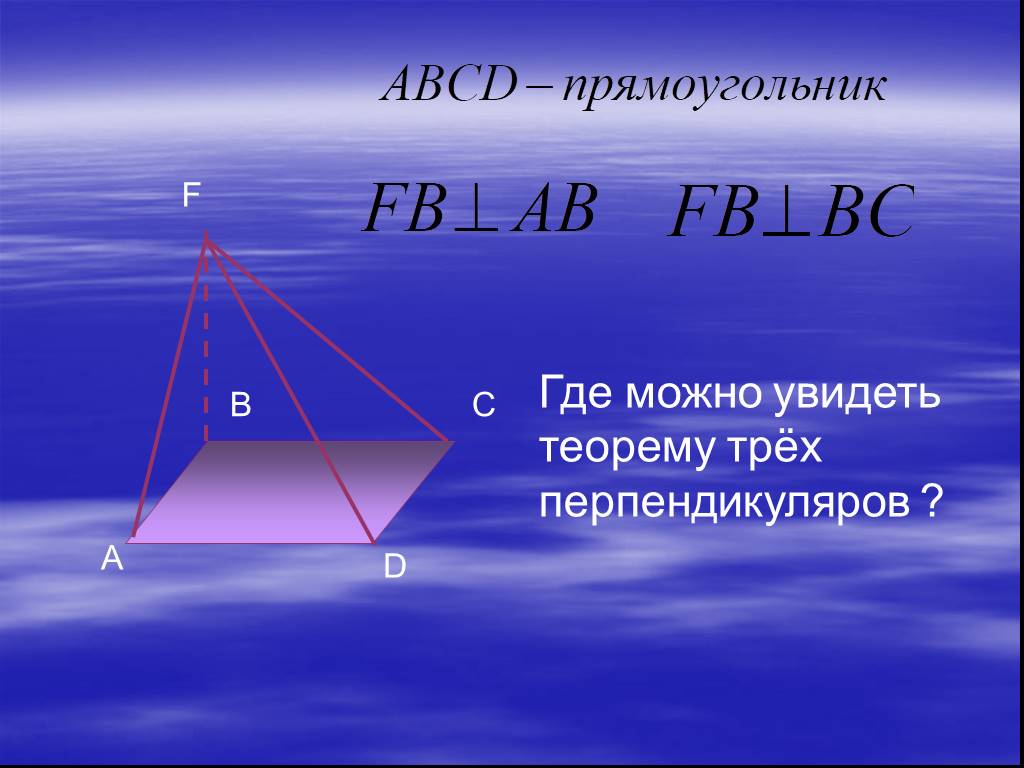
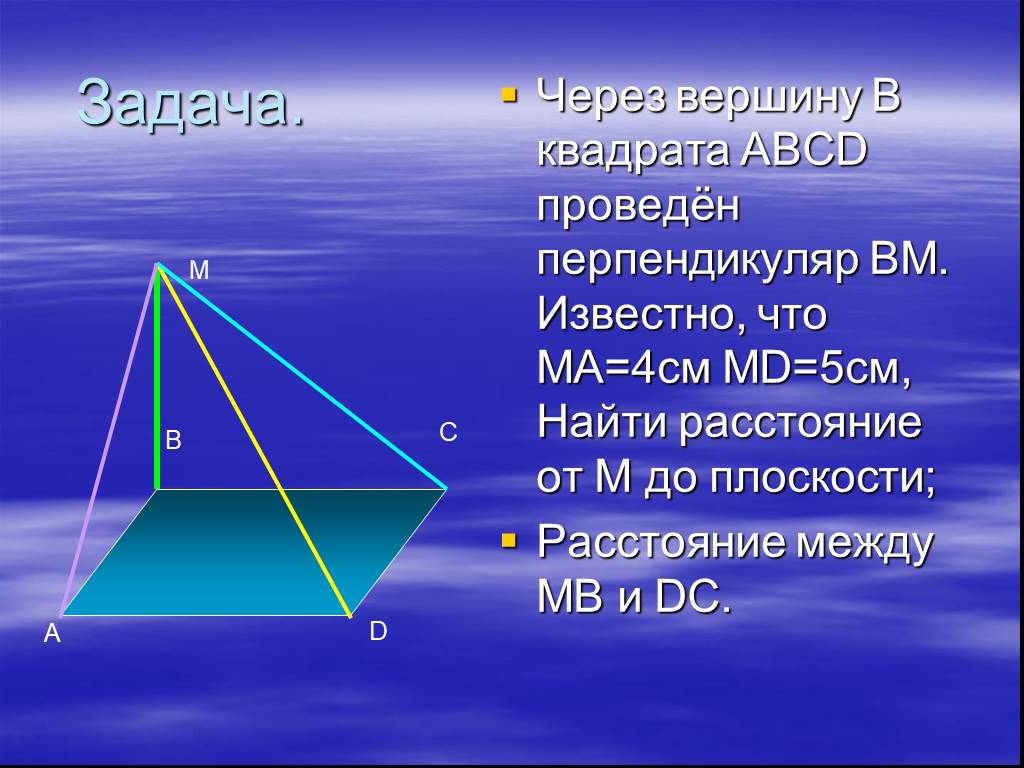
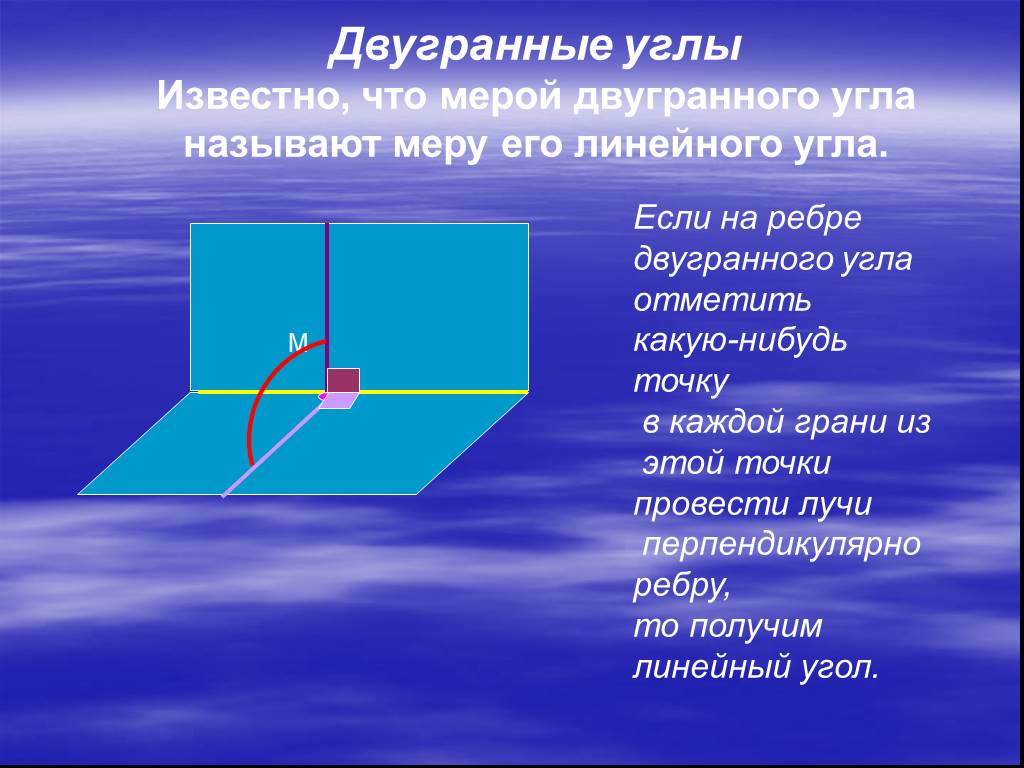
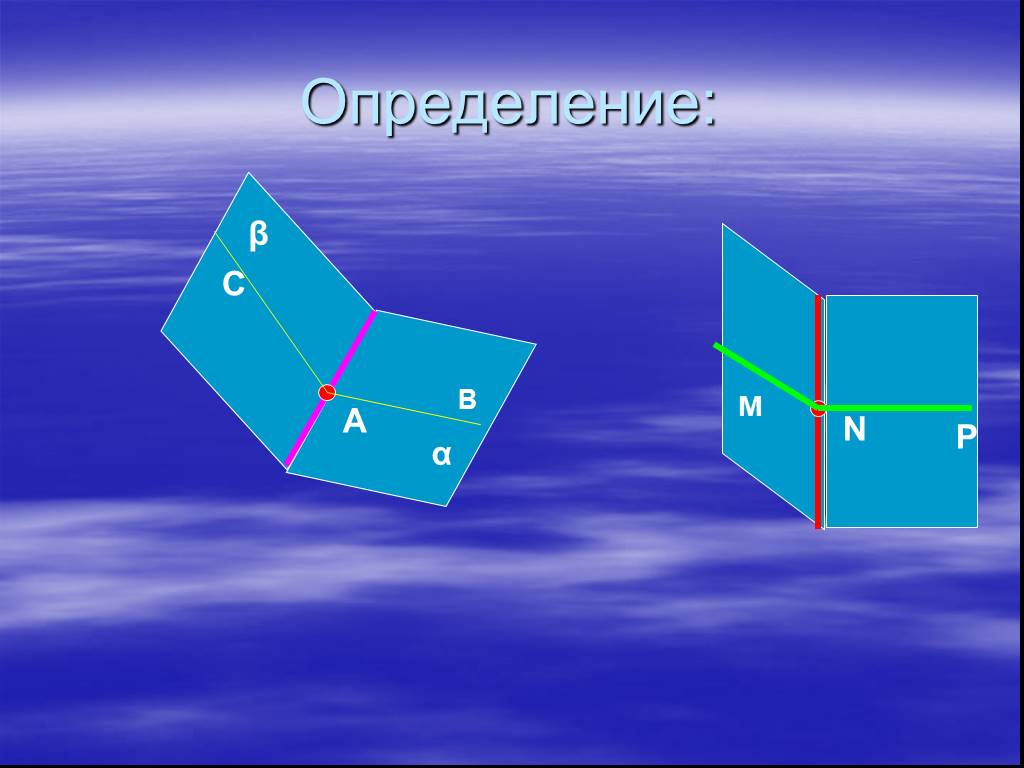
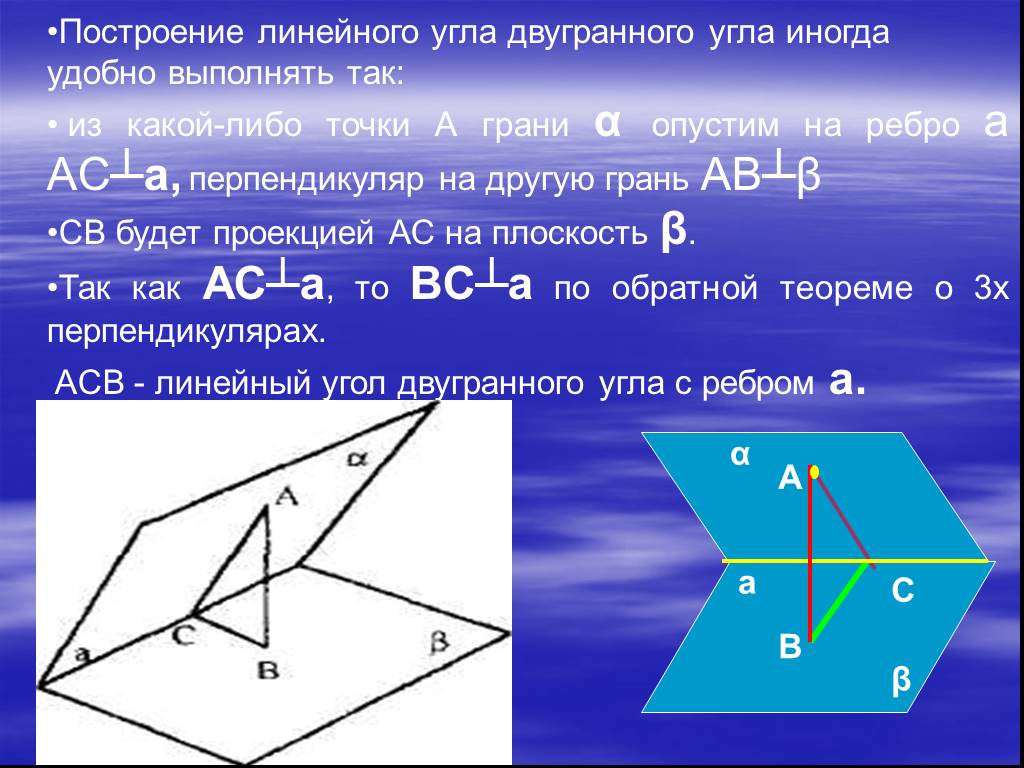
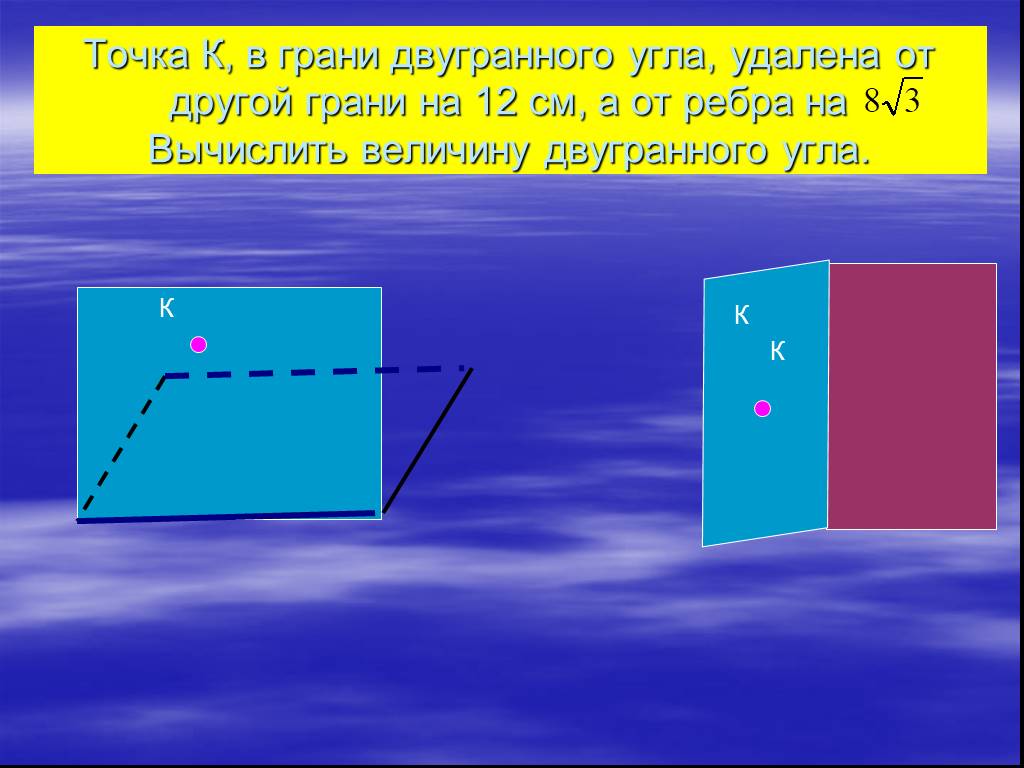
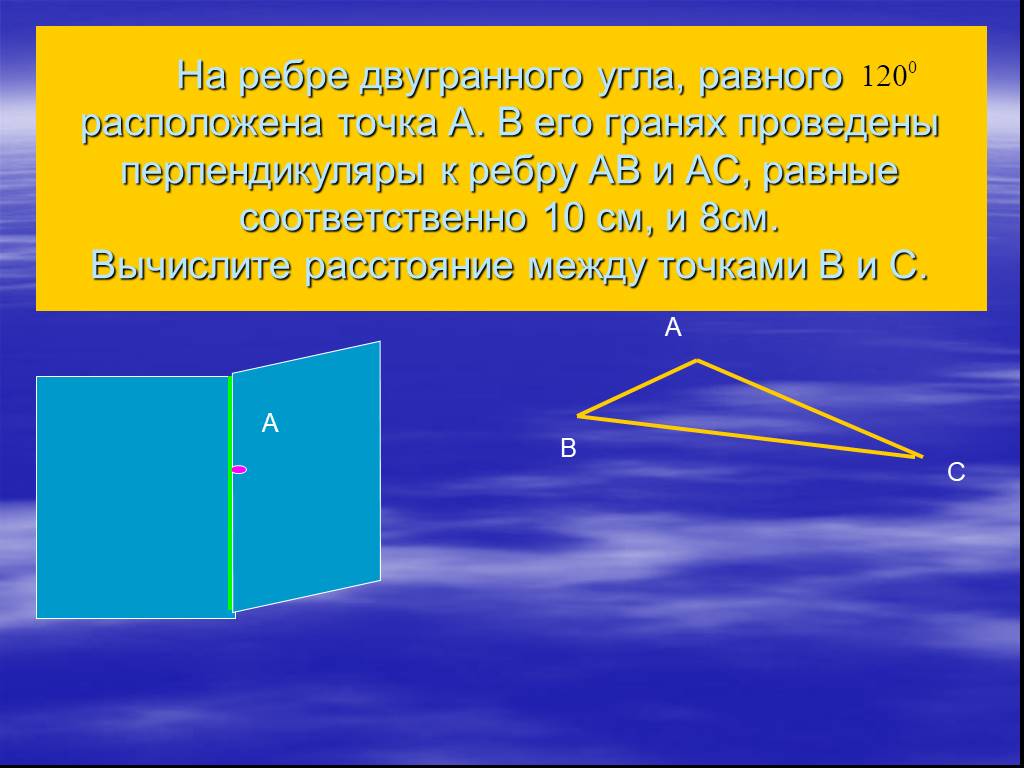
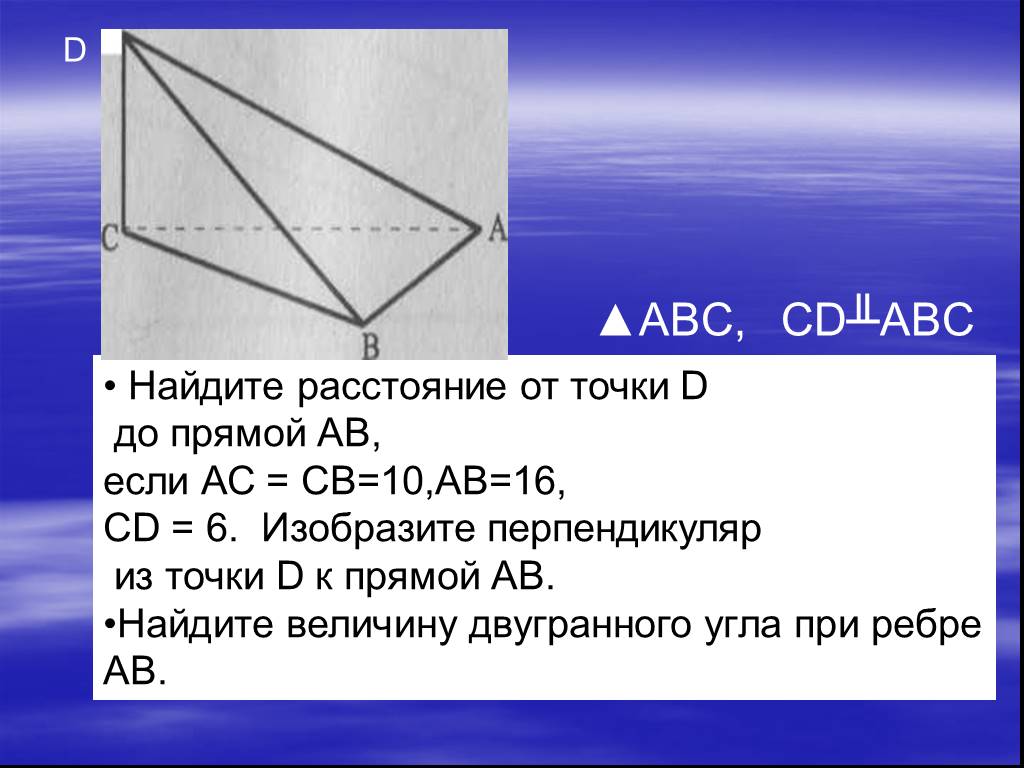
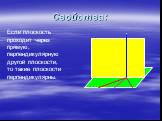
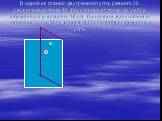
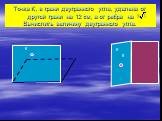
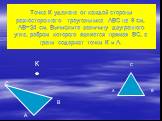
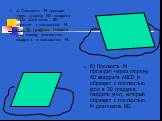
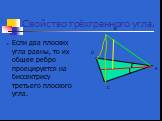
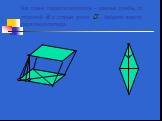
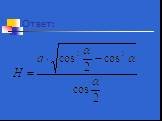
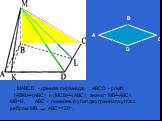
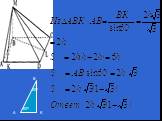
Презентация "Определение двугранных углов" по математике – проект, доклад
Презентацию на тему "Определение двугранных углов" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 50 слайд(ов).
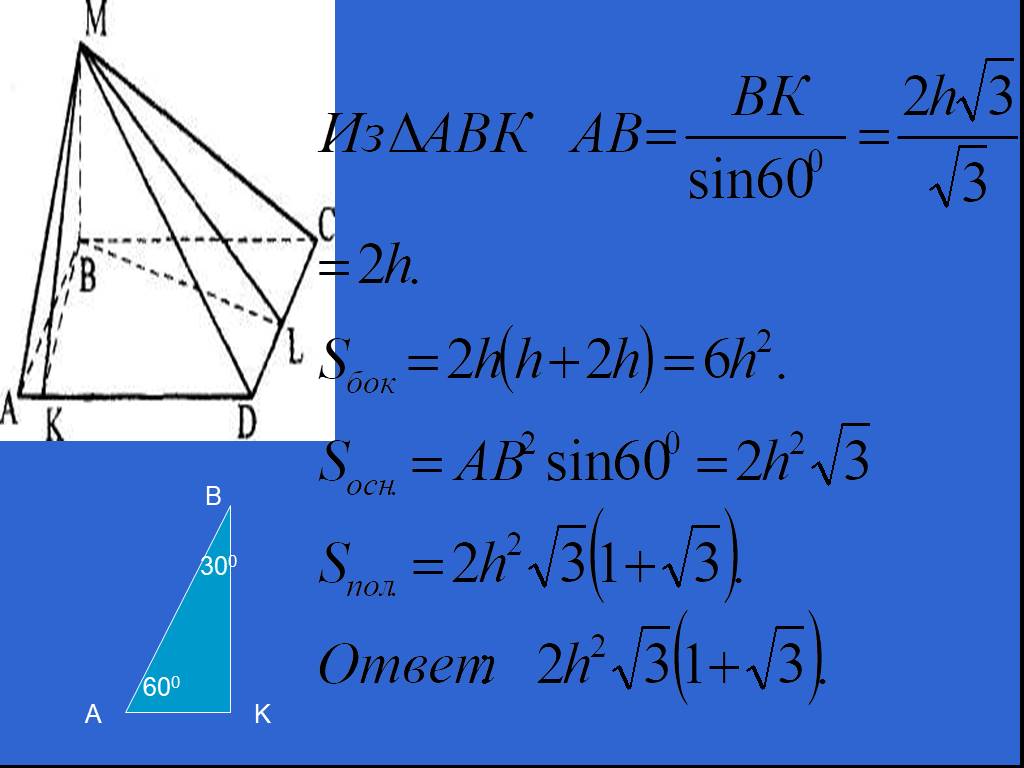
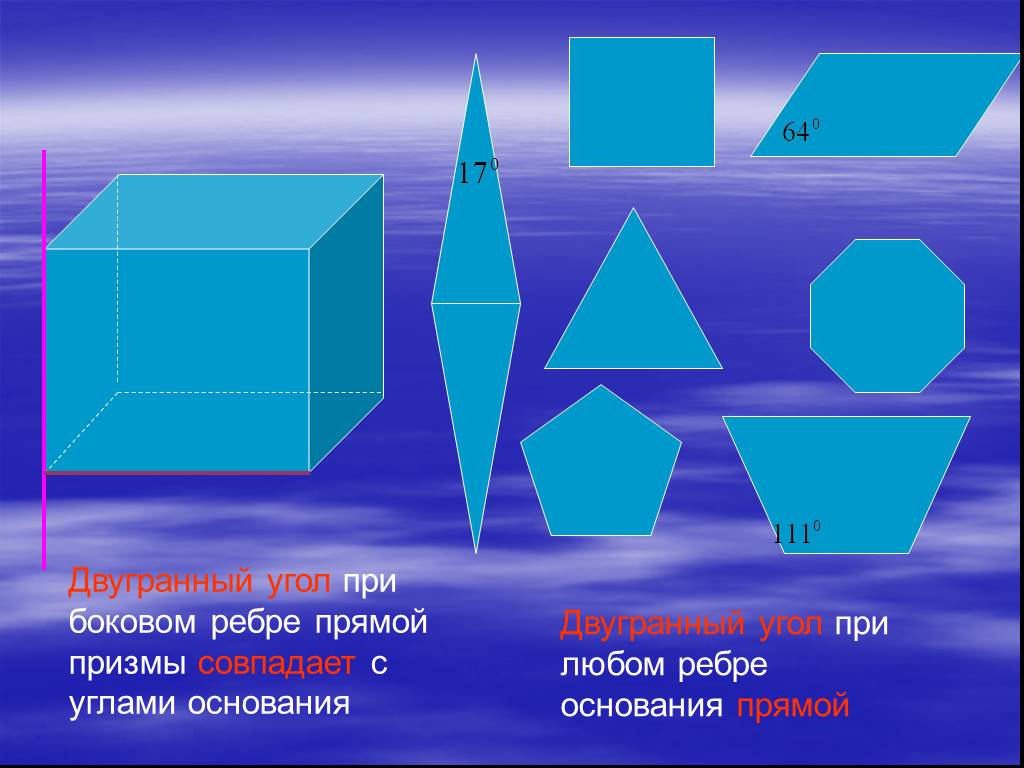
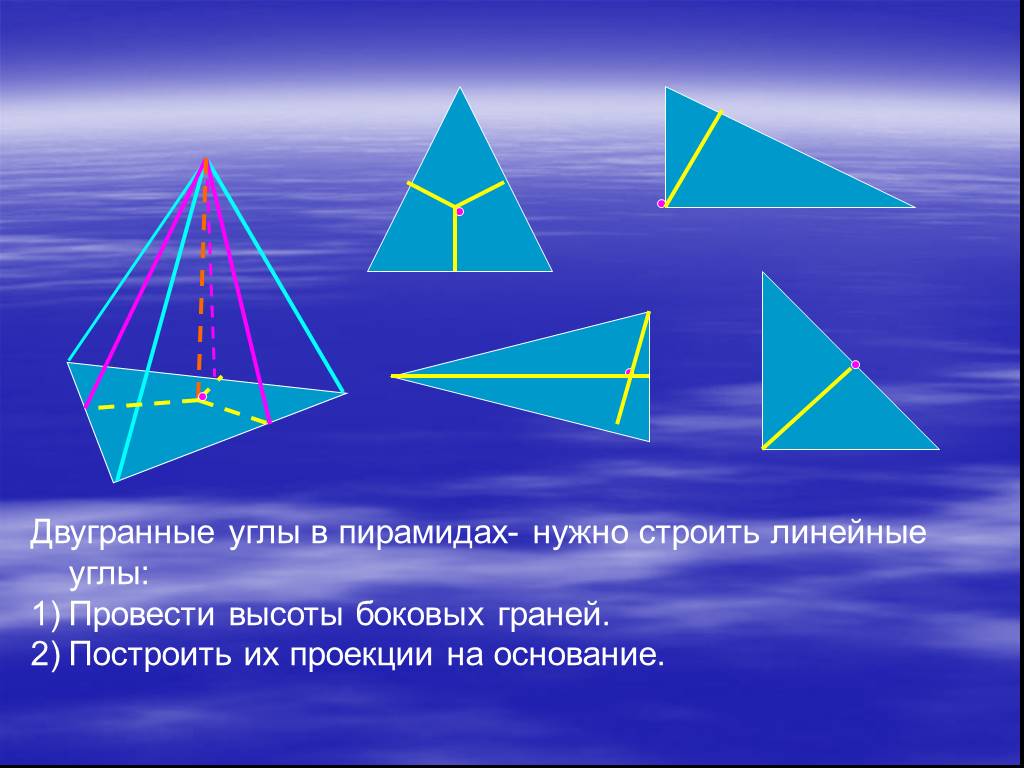
Слайды презентации
Список похожих презентаций
Определение синуса, косинуса, тангенса и котангенса углов поворота
x y 1 0. Вспомним, что любая точка координатной плоскости имеет две координаты – абсциссу и ординату:. y – ордината точки M. x – абсцисса точки M. ...Сравнение углов
Математика. Я упомянул о математике как о способе приучить ум к точному и последовательному мышлению. Я не хотел этим сказать, что, по моему мнению, ...Свойство углов треугольника
Виды треугольников. B A C E F D N M K Остроугольный Прямоугольный Тупоугольный. Верно ли, что:. - остроугольный треугольник – это треугольник у которого ...Построение углов
Цель:. учить измерять углы; учить строить углы заданной градусной величины. Вспомним! сторона вершина А В О АОВ, ВОА, О. Виды углов развёрнутыйугол. ...Определение чисел arcsina, arccosa,arctga, arcctga
План. Теорема о корне монотонной функции Возрастание синуса на отрезке [−π/2; π/2] Определение арксинуса числа График синуса на отрезке [−π/2; π/2] ...Устные упражнения на уроках геометрии. Свойства смежных и вертикальных углов
Ответ. 105о. . . . . . 116о. 50о. . 60о. 40о. ...Тригонометрические функции углов в произвольном треугольнике 1-2
Продолжите фразу:. Синусом острого угла прямоугольного треугольника называется. А С В. отношение противолежащего катета к гипотенузе. Косинусом острого ...Сумма углов треугольника
. Решите устно А В С 1 2 4 5 6 7 8 Е D ? 4= 6 2= 1= 5= 8 5=70°, 4=30° 70° 80° } 180°. Теорема о сумме углов треугольника. Эпиграф. Легче остановить ...Измерение углов
I. Проверочная самостоятельная работа (проверка усвоения свойств длин отрезков) (10 минут). II. Новый материал. 1. Измерение углов аналогично измерению ...Измерение углов
I. Проверочная самостоятельная работа (проверка усвоения свойств длин отрезков) (10 минут). II. Новый материал. 1. Измерение углов аналогично измерению ...Измерение углов
А В. С М N K. Равные углы имеют равные градусные меры. . Меньший угол имеет меньшую градусную меру. О Р. Если луч делит угол на два угла, градусная ...Значения синуса, косинуса, тангенса для углов 30, 45, 60
Устный счёт В а с С b А. закрепление. В 1 С 2 А 1) Найти ответы: 2) Найти 3)Найти 4)Найти 5)Найти 6)Найти. Изучение нового материала. В 2a угол А ...Значение синуса, косинуса и тангенса для углов 30°, 45°, 60°
Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. AB² = AC² + BC². Синусом острого угла прямоугольного ...ГИА-2012. Решение планиметрических задач на нахождение углов геометрических фигур
1 3 4 5 6 7 8 9 10 11. Вашему вниманию представлено двенадцать прототипов задачи № 11 Открытого банка заданий по математике. ГИА – 2012. Два острых ...Сумма углов в треугольнике
Устная работа На рисунке 1=51, 2=129, 3=52, ВЕ – биссектриса угла АВС. Найдите угол 4. ПРАКТИЧЕСКАЯ РАБОТА. Сумма углов треугольника равна 180. УСТНАЯ ...Сумма углов треугольника
5º, 12º, 104º, 33º, 99º, 178º, 4º, 95º,180º, 89º, 23º, 125º, 11º,76º, 1º. Определи виды углов. Устный счёт. Прочитайте чертёж. 2 1 40° 150° ? 140° ...Измерение углов
За единицу измерения углов обычно принимается угол, составляющий одну сто восьмидесятую часть развернутого угла. Считают, что величина этого угла ...Теорема о сумме углов треугольника
A C. Найдите углы треугольников:. B D 50˚ 120˚. Дано: BD AC Найти: 1 2 4 5. Теорема: Сумма углов треугольника равна 180˚. Дано: ▲ABC Треб. док. : ...Измерение углов
Действия с десятичными дробями. Разминка. Какой знак можно поставить в следующих примерах? 0,21 + 105 2 цифры 1 цифра 3 цифры 21 5 0,735 0 - 70. 0,52 ...Угол. Виды углов
Единица измерения времени.2. Единица измерения массы.
3. Сотая часть числа.
4. Инструмент для измерения длины отрезков.
М И Н У Т А Г Р П О Ц ...
Конспекты
Сумма углов треугольника
Урок по геометрии в 7 классена тему: «Сумма углов треугольника». Тип урока:. урок изучения нового материала.Цели урока:. Образовательные:. доказать ...Сумма углов треугольника
Урок по теме «Сумма углов треугольника», 7 класс. . Ладанова И.В. – учитель математики. . МКОУ «Верх-Жилинская ООШ». Косихинский район Алтайский ...Сумма углов треугольника
ПЛАН-КОНСПЕКТ УРОКА Сумма углов треугольника. . . ФИО (полностью). . Нагорнова Елена Владимировна. . . . . Место работы. . ...Сумма углов треугольника
Муниципальное казенное общеобразовательное. . учреждение лицей №11. Открытый урок в 7 классе по теме:. Сумма углов треугольника. Подготовила ...Определение числовой функции. Область определения, область значений функции
Муниципальное общеобразовательное учреждение. Оковецкая средняя общеобразовательная школа. Селижаровский район Тверская область. Тема урока:. ...Сумма углов треугольника
Методический портал учителя «Методсовет» - http. ://. metodsovet. . su. . Автор: Морина Светлана Алексеевна. Учитель математики МБОУ СОШ ...Виды углов
Тема урока: «Виды углов». 4 класс. Учитель: Л.А.Локтева. Целевые установки: Предметные. Классифицировать углы на острые, прямые и тупые; использовать ...Виды углов
Проект занятия. Класс 2. Тип занятия - занятие «открытия» нового знания. Особенности данного занятия. . Данное занятие проводится в ...Виды углов
Муниципальное общеобразовательное учреждение. «Дубовская средняя общеобразовательная школа. Белгородского района Белгородской области. с углублённым ...Виды углов
Мисуно Татьяна Владимировна. учитель начальных классов Аккайинской ОШ. первой категории. урок по математике в 4 классе. Тема. :. Виды углов. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:6 февраля 2019
Категория:Математика
Содержит:50 слайд(ов)
Поделись с друзьями:
Скачать презентацию