Презентация "Основные понятия комбинаторики" по математике – проект, доклад
Презентацию на тему "Основные понятия комбинаторики" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 14 слайд(ов).
Слайды презентации
Список похожих презентаций
Основные принципы комбинаторики
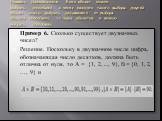
Комбинаторика. Комбинаторика – раздел математики, посвященный подсчету количеств разных комбинаций элементов некоторого, обычно конечного, множества ...Основные понятия
В задачах на смеси, растворы и сплавы основными понятиями являются: «концентрация», «процентное содержание», «закон сохранения массы», «закон сохранения ...Основные понятия криптографии
Криптология Криптография Криптоанализ Открытый текст. Криптограмма (шифртекст). Шифр Ключ Стойкость шифра назад. Работай с диаграммой. (от греч. cryptos ...Основные понятия, связанные с квадратными уравнениями
Квадратное уравнение. Из данных уравнений выберите квадратные:. ПРИВЕДЕННЫЕ НЕПРИВЕДЕННЫЕ ? ПОЛНЫЕ НЕПОЛНЫЕ. Решение неполных квадратных уравнений. ...Основные понятия теории вероятности
Теория вероятностей. Введение. Основные комбинаторные объекты. Элементы теории вероятности. Задачи в которых производится подсчет всех возможных комбинаций ...Основные понятия дроби
Закрепить понятие алгебраической дроби; Научить составлять математическую модель задачи; Научить находить значение алгебраической дроби, находить ...Наукометрия: история и основные понятия
Немного истории 1965 год. 1955 год – Юджин Гарфилд создает Институт научной информации (ISI). 1961 год – Science Citation Index и Journal Citation ...Основные понятия и определения
Основные понятия и определения. Система — объединение элементов, образующих связное целое. Элемент — объект, учитываемый внешними связями и не разлагаемый ...Логарифм. Основные понятия
. . . . Десятичные логарифмы. Логарифмы по основанию 10 (обозначение: lg a) до изобретения калькуляторов широко применялись для вычислений. Неравномерная ...Основные фигуры
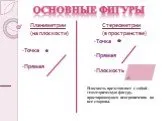
А В С Е. Точки обозначаются прописными латинскими буквами А, В, С, D, Е, К,…. Планеты и звезды в масштабе вселенной. Птицы и самолеты в небе. Атомы ...Основные тригонометрические функции
Пояснительная записка. В результате изучения курса математики учащиеся должны понимать, что функция – математическая модель, позволяющая описывать ...Основные типы задач на проценты
Цели урока: вспомнить основные понятия из курса математики по теме «Проценты»; сформировать понимание процента как специального способа выражения ...Владимирская область через математические понятия
Кроссворд № 1. 1. Направленный отрезок прямой. 2. Это множество точек плоскости, находящихся на данном расстоянии от данной точки, лежащей в той же ...История введения понятия функции в школьный курс математики и современность
Функция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира. Во второй половине ...Базовые понятия математической статистики
Описательная статистика. Локализация Среднее значение Медиана Мода. Дисперсия Перцентиль Межквартильный размах Размах признака Дисперсия Стандартное ...История развития понятия функции
История развития понятия функции. Функция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании ...Проценты. Основные задачи на проценты
Как пользоваться данным пособием:. Внимательно читайте каждое правило Обращайте внимание на предложенные примеры В конце пособия даны задания для ...Методика изучения элементов комбинаторики в условиях профильного обучения математике
Содержание. Введение Глава 1. Цели изучения стохастической линии в школе 1) Из истории комбинаторики 2) Цели изучения стохастики в школе Глава 2. ...Математические понятия и методика их изучения в школьном курсе математики
План. Математические понятия (сведения из логики) Сущность математических понятий; Логические характеристики понятий: содержание, объем; Пути конструирования ...Математические понятия
Введение. Понятие является одной из главных составляющих в содержании любого учебного предмета, в том числе – и математики. Объект исследования: процесс ...Конспекты
Квадратные уравнения. Основные понятия. Решение неполных квадратных уравнений
Тема:. «Квадратные уравнения. Основные понятия. Решение неполных квадратных уравнений». Тип урока:. урок изучения нового материала. Цели урока:. ...Элементы комбинаторики, статистики и теории вероятности
Урок-соревнование. по разделу. «Решение задач по теме «Элементы комбинаторики, статистики и теории вероятности». г.Новороссийск, ...Самые важные понятия математики
Интегрированный урок (математика + история). в 5 классе по. теме «Самые важные понятия математики». Л.Н. Головина, учитель математики. Заречненской ...Простейшие геометрические понятия
Емцева Юлия Ивановна. . Гимназия №33 г.Краснодара. . Учитель начальных классов. . . Урок математики в 1 классе. (здоровьесберегающие ...Применение понятия периодической функции
РАЗРАБОТКА УРОКА. учителя математики МОУ гимназии № 35 г.о. Тольятти. Батаевой Галины Александровны. Предмет: алгебра и начала анализа. Класс: ...Основные приемы решения задач на сплавы, смеси, растворы
Афанасьева Елена Викторовна. МБОУ СОШ№12, г.Ноябрьск. учитель математики. . Тема:. . «Основные приемы решения задач на сплавы, смеси, растворы». ...Основные методы решения тригонометрических уравнений
. МАТЕМАТИКА 11 класс. Тема: Основные методы решения тригонометрических уравнений. Цели урока:. Обобщить и систематизировать полученные знания ...Действия с обыкновенными дробями. Основные задачи на дроби
ГБС(К)ОУ ШИ. I. -. II. вида г. Тихорецка Краснодарского края. Урок – КВН. в 7 классе по теме:. «Действия с обыкновенными дробями. Основные ...Введение понятия процента
АВТОР: Руденко Наталья Николаевна ,учитель математики МОУ «СОШ №15 имени В.Л. Гриневича» города Прокопьевск. Тема урока: «. Введение понятия процента. ...Введение понятия первообразной
. Муниципальное общеобразовательное учреждение. «Средняя общеобразовательная школа №7. г. Соль-Илецка Оренбургской области». ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 января 2019
Категория:Математика
Содержит:14 слайд(ов)
Поделись с друзьями:
Скачать презентацию