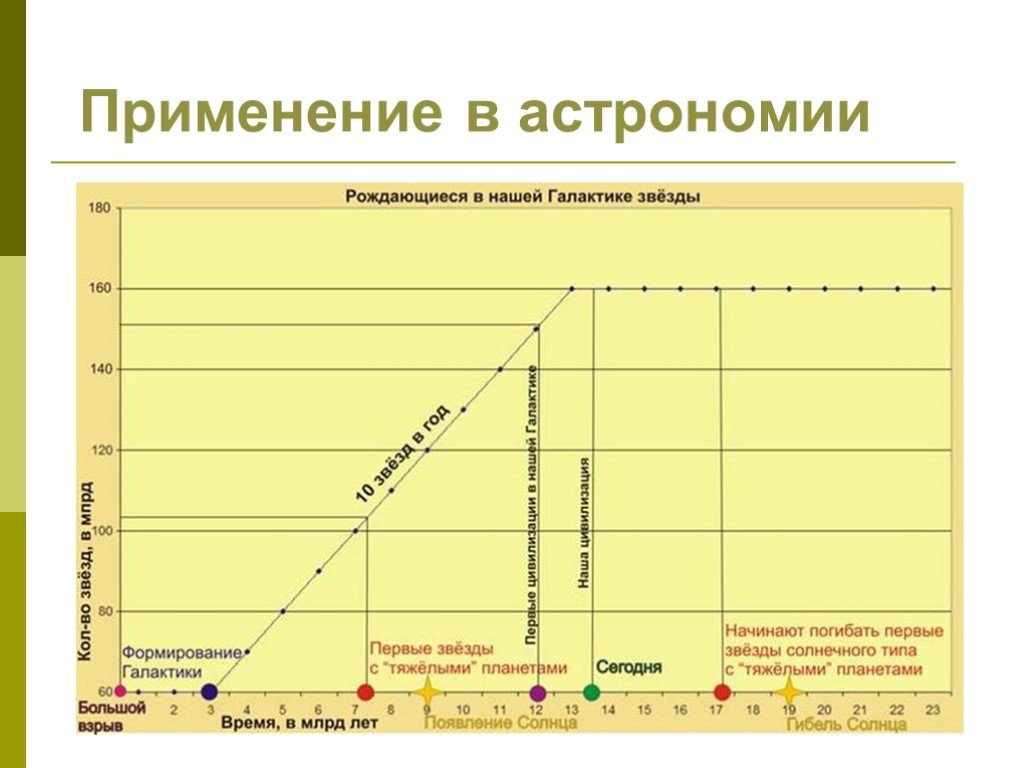
Презентация "История развития понятия функции" по математике – проект, доклад
Презентацию на тему "История развития понятия функции" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 33 слайд(ов).
Слайды презентации
Список похожих презентаций
История развития понятия функции
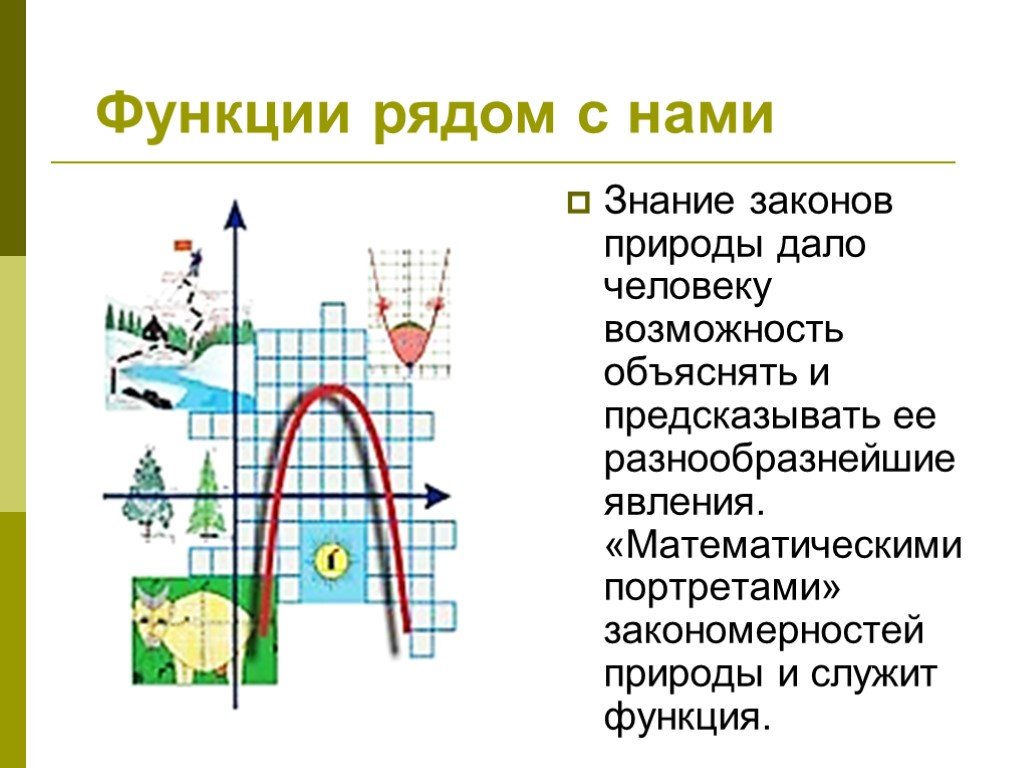
Функции, как и живые существа, характеризуются своими особенностями. П. Монтель. Идея функциональной зависимости восходит к древности. Ее содержание ...История введения понятия функции в школьный курс математики и современность
Функция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира. Во второй половине ...История развития тригонометрии
Слово тригонометрия впервые встречается в 1505 году в заглавии книги немецкого математика Питискуса. Тригонометрия – слово греческое и в буквальном ...История развития математики
Палеолит. Первоначальные представления о числе и форме. Неолит. Развитие ремёсел: Гончарное Ткацкое Плотническое. Счёт австралийских племён:. Племя ...История развития математики
Содержание Математика - это ? Возникновение арифметики и геометрии. Древний Восток Вавилон Древняя Греция Заключение. Математика - это наука, исторически ...История возникновения и развития математики"
«Учиться можно только весело … Чтобы переваривать знания, надо поглощать их с аппетитом» Анатоль Франс. Цели урока:. 1.Обобщить начальные сведения ...История развития геометрии
ВВЕДЕНИЕ:. Геометрия возникла очень давно, это одна из самых древних наук. Геометрия (греческое, от geо — земля и metrein — измерять) - такое название ...Наукометрия: история и основные понятия
Немного истории 1965 год. 1955 год – Юджин Гарфилд создает Институт научной информации (ISI). 1961 год – Science Citation Index и Journal Citation ...История возникновения и развития математики
ХОД ИГРЫ. 1. Решить уравнения: а)4,7y-(2,5y+12,4)=1,9 б)3,5x-(2,3x-3,8)=4,28. «Первая тройка». Витя Верхоглядкин отыскал правильную дробь, которая ...Взаимное расположение графиков линейной функции
Разбейте функции, заданные формулами, на группы:. у = 2х - 3; у = х2 - 3; у = - 5х; у = 4 - 0,5х; у = - х +2; у=15х;. 7. 8. 9. 10. у = х (1 - х). ...Основные понятия теории вероятности
Теория вероятностей. Введение. Основные комбинаторные объекты. Элементы теории вероятности. Задачи в которых производится подсчет всех возможных комбинаций ...Коэффициенты квадратной функции
Предисловие. В данном проекте автор специально не использовал теоретическое обоснование, а только выводы на их основе. Для более глубокого и полного ...Наибольшее и наименьшее значения функции
(x²)′= (2x³)′= (7x)′= (10)′= (128 )′= (5x² + 3x - 9 )′= x² 6x² 0 7 10x + 3. АЛГОРИТМ.Найти точки экстремума функции, т. е. точки в которых производная ...
Взаимно обратные функции
Цель проекта: Изучить поведение взаимно обратных функций. Установить связь графиков прямой и обратной функций. Подготовиться к успешной сдаче ЕГЭ. ...История чисел и системы счисления
Содержание. Понятие «системы счисления» История чисел Виды систем счисления Непозиционные системы счисления Позиционные системы счисления Арабская ...Геометрические понятия
"Начала" (ОК. 365-360Г. ДО Н. Э) Эвклид. Одна из легенд рассказывает, что царь Птолемей решил изучить геометрию. Но оказалось, что сделать это не ...Приёмы развития интеллектуальных умений и творческих способностей младших школьников на уроках математики
Творческие способности —. особый вид умственных способностей, выражающихся в умении продолжать мыслительную деятельность за пределами требуемого, ...Возрастание и убывание функции
Числовые промежутки. [α;b] – отрезок (α;b) – интервал (α;b] – полуинтервал [α;b) - полуинтервал. Функция f(x) называется возрастающей на некотором ...Вычисление производной функции
При вычислении производной функции, будем иметь в виду, что один из способов найти производную - это взять достаточно малые значения справа и слева ...Влияние коэффициентов а, b и с на расположение графика квадратной функции
Определите, график какой функции изображен на рисунке:. у = х² – 2х – 1; у = –2х² – 8х; у = х² – 4х – 1; у = 2х² + 8х + 7; у = 2х² – 1. у = ½х² – ...Конспекты
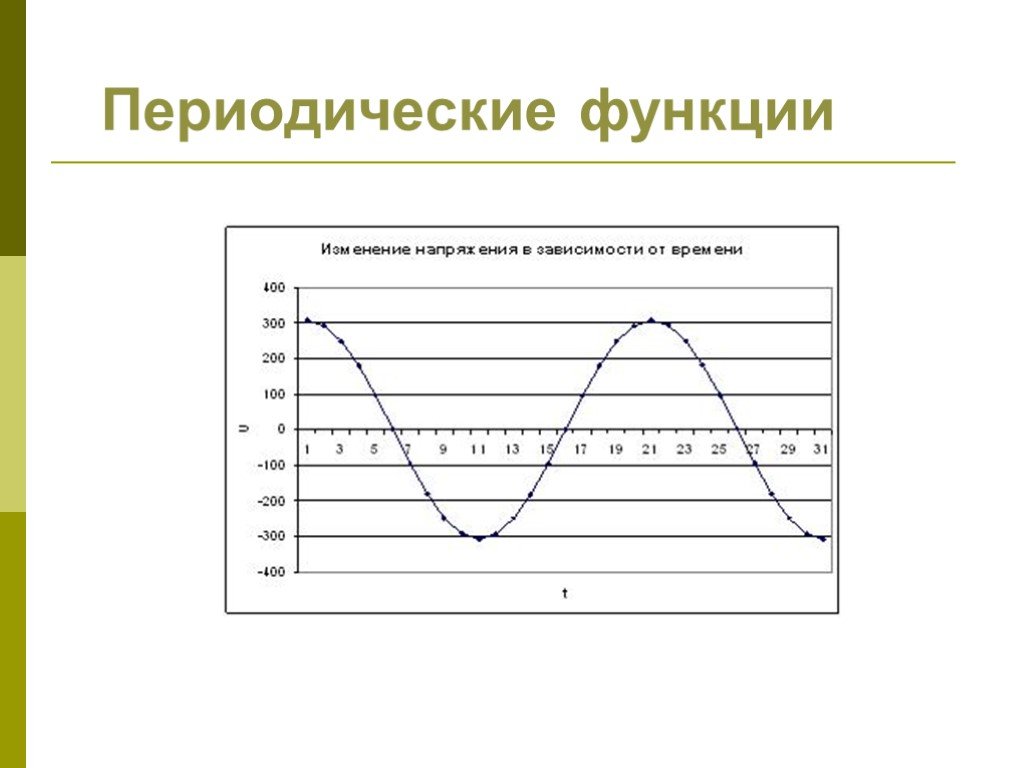
Применение понятия периодической функции
РАЗРАБОТКА УРОКА. учителя математики МОУ гимназии № 35 г.о. Тольятти. Батаевой Галины Александровны. Предмет: алгебра и начала анализа. Класс: ...История возникновения и развития геометрии. Начальные геометрические сведения
Урок геометрии с использованием ИКТ. . Класс:. 7. Учитель:. Петрова Марина Николаевна,. учитель математики МБОУ СОШ №76. . Орджоникидзевского ...Преобразование графика тригонометрической функции у = sin x путем сжатия и расширения
Предмет:. алгебра 10 кл. Тема урока:. «Преобразование графика тригонометрической функции у = sin. x. путем сжатия и расширения». Тип урока:. ...Построение графика квадратичной функции с использованием сдвигов по осям координат
МБОУ Чистопольская СОШ. Урок алгебры в 8 классе. Тема «Построение графика квадратичной функции с использованием сдвигов по осям координат». ...Построение графика квадратичной функции
Учитель: Рогачева Татьяна Викторовна. Место работы: ГОУ СОШ №103, Санкт-Петербург. Должность: Учитель математики. Урок алгебры в 9 классе. . ...Чётность и нечётность функции
Урок по теме : Чётность и нечётность функции. 9-й класс. Учитель математики: Семенова Н.Н. Цель урока:. рассмотреть свойство графиков чётной ...Степенные функции, их свойства и графики
Тема урока:. . «Степенные функции, их свойства и графики». . Цели урока:. . Образовательная:. Создать условия для закрепления знаний о свойствах ...Простейшие геометрические понятия
Емцева Юлия Ивановна. . Гимназия №33 г.Краснодара. . Учитель начальных классов. . . Урок математики в 1 классе. (здоровьесберегающие ...Возрастание и убывание функции
Муниципальное общеобразовательное учреждение. . Копорская средняя общеобразовательная школа. Ленинградской области. КОНСПЕКТ УРОКА. ...Возрастание и убывание функции
Муниципальное бюджетное общеобразовательное учреждение. гимназия №19 им Поповичевой Н.З., г. Липецка. Конспект урока по алгебре в 9 классе (политехнический ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:17 ноября 2018
Категория:Математика
Содержит:33 слайд(ов)
Поделись с друзьями:
Скачать презентацию