Презентация "Определение чисел arcsina, arccosa,arctga, arcctga" (11 класс) по математике – проект, доклад
Презентацию на тему "Определение чисел arcsina, arccosa,arctga, arcctga" (11 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 26 слайд(ов).
Слайды презентации
Список похожих презентаций
Определение первообразной
Определение первообразной. Цели урока: Повторить правила дифференцирования; Ввести определение первообразной; Научить учащихся применять определение ...Определение запыленности воздуха по листьям деревьев с использованием формулы Пика
Введение. В последние годы, наряду с изменениями климата, происходит значительное увеличение антропогенной нагрузки на природные и урбанизированные ...Определение конуса
Круговым конусом называется тело ограниченное кругом – основанием конуса, и конической поверхностью, образованной отрезками, соединяющими точку, вершину ..."Сложение положительных и отрицательных чисел"
Старостенко Алла Николаевна, учитель математики Предмет: математика, урок-игра, закрепление изученного материала Тема: «Сложение положительных и отрицательных ...Округление чисел
Решив эти примеры вы узнаете нечто интересное. Округлите до десятых:. 0,685≈ 1,544≈ 5,628≈. Округлите до сотых:. 7,46786≈ 2,21910≈ 4,735102≈ 87,5314≈ ...Последовательность чисел
Дни недели Названия месяцев Классы в школе. Номер счёта в банке. Дома на улице. Последовательности составляют такие элементы природы, которые можно ...Примеры многозначных чисел
ПЯТИЗНАЧНЫЕ И ШЕСТИЗНАЧНЫЕ ЧИСЛА. РЕШЕНИЕ ЗАДАЧ. Задание 264. или = ? 1) 3 • 1000 ... 1000 + 1000 +1000 2) 5 • 1000 ... 1000 + 1000 + 1000+ 1000 ...В мире чисел
Корни нумерологии. 1. Качества: благость, желательность, необходимость, неделимость. Связывалась с Аполлоном, Прометеем Символизирует начинание, источник, ...Влияние "главных чисел" на характер человека
Эпиграф. Мысль выражать все числа знаками настолько проста, что именно из – за этой простоты сложно осознать, сколь она удивительна. Пьер Симон Лаплас. ...Бесконечный мир чисел
Когда родилась математика, и что явилось причиной ее возникновения? Существует два мнения о возникновении математики. Первое – что математика возникла ...В мире чисел
Математика — это наука, имеющая дело с числами, количеством, формой. Без знания математики вся современная жизнь была бы невозможна. Например, у нас ...Арифметическая теория действительных чисел по Мерэ-Кантору
Георг Кантор (3 марта 1845г. – 6 января 1918г.). Георг Фердинанд Людвиг Филипп Кантор родился 3 марта 1845 г. в России, в Санкт-Петербурге. Его мать, ...Алгоритм письменного сложения и вычитания многозначных чисел
Сможете ли вы выполнить задание для любознательных? Восстанови примеры. + * 8 7 * - 3 * 1 * 4 3 * 1 8 7 2 6 * * 0 2 * 1 * 8 * 0 6. 10 единиц = 1 десяток ..."Умножение и деление чисел"
Тема урока:. Умножение и Деление чисел. В наше время, чтобы строить И машиной управлять, Помни друг, что надо прочно Математику познать! Математический ...Определение степени с натуральным показателем
«Веселые старты» среди 1-2 классов. «Веселые старты» среди 3-4 классы. Шахматы среди 5-х классов. Настольный теннис среди 6-7 классов. Баскетбол среди ...Всё об округлении чисел
Содержание. Что такое «округление числа» Округление целых чисел Округление десятичных дробей Для самостоятельного решения. Определение. Округление ...Перевод целых чисел из десятичной системы счисленияв другие системы счисления
Сколько лет каждому из вас в 8-ричной или 16-ричной системах счисления? «10», «11», «100», «101» - такой была бы шкала оценок в школе в двоичной системе ...Вычитание двузначных чисел
НОВОЕ ЗНАНИЕ (понятие, способ действия) и его фиксация (эталон). Алгоритм вычитания двузначных чисел с переходом через разряд. ПРОБНОЕ ДЕЙСТВИЕ. Найти ...Прибавление чисел
Вставить пропущенные числа. 3, •, 5, •, 7, •, 9, 10 10, •, 8, •, 6, 5, •,3, •, 1. Назвать соседей чисел. • 13 • • 9 • • 6 • • 10 • • 8 • • 4 •. Сравнить ...Вычитание двузначных чисел
16-7=9. 15-7 12-7 11-9 12-3 12-8 11-8 15-8 15-9 и в а н у ш к. 74-12 65-22 41-24 76-9. Алгоритм. Пишу единицы под единицами, а десятки – под десятками. ...Конспекты
Нумерация многозначных чисел, письменное сложение и вычитание
Открытый урок математики для студентов пед. коледжа №5. . . Учитель: Коновалова В.А. Класс: 3-А. Программа Л.Г.Петерсон. Тема урока: «Нумерация ...Модуль числа. Сравнение чисел
Конспект урока для 6 класса «Модуль числа. Сравнение чисел». ТЕМА УРОКА:. Цели урока:. . Обучающая:. повторить определение модуля и правила ...Натуральный ряд чисел
5. . . Тема:. «Натуральный ряд чисел. ». (подготовила и провела Терентьева Н.П., 1класс). . Цель: дать понятие о натуральном ряде чисел,. ...Письменное сложение и вычитание трёхзначных чисел
Тема:. Письменное сложение и вычитание трёхзначных чисел. . . Цели:. Познакомиться с алгоритмом письменных приёмов сложения и вычитания трёхзначных ...История возникновения чисел. Магическое значение чисел в нашей жизни
. Научно-практическая конференция школьников. . «Шаг в науку». секция «Математика». . История возникновения чисел. ...Округление натуральных чисел
. ПЛАН-КОНСПЕКТ УРОКА Округление натуральных чисел. (Тема урока). ФИО. . . Иванюра Валентина Николаевна. . . Место работы. ...Определение степени с натуральным показателем
Урок алгебры в 7 классе. . по теме «Определение степени с натуральным показателем». . в рамках проведения. . Всероссийского открытого урока ...Вычитание двузначных чисел
Тип урока:. ОНЗ. Тема: «Вычитание двузначных чисел». Основные цели:. 1) сформировать представление о вычитании двузначных чисел;. 2) актуализировать ...Вычитание двузначных чисел
МБОУ «Ярцевская средняя общеобразовательная школа №9». Образовательная система «Начальная школа 21 века». Конспект. урока математики ...Внетабличное умножение и деление чисел
Открытый урок. математики . 3 класс. тема:. «Внетабличное умножение и деление чисел». . Разработала учитель. начальных ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:29 апреля 2019
Категория:Математика
Содержит:26 слайд(ов)
Поделись с друзьями:
Скачать презентацию
























![План. Теорема о корне монотонной функции Возрастание синуса на отрезке [−π/2; π/2] Определение арксинуса числа График синуса на отрезке [−π/2; π/2] Примеры Определение арккосинуса числа Определение арктангенса числа Определение арккотангенса числа План. Теорема о корне монотонной функции Возрастание синуса на отрезке [−π/2; π/2] Определение арксинуса числа График синуса на отрезке [−π/2; π/2] Примеры Определение арккосинуса числа Определение арктангенса числа Определение арккотангенса числа](https://prezentacii.org/upload/cloud/19/04/142715/images/thumbs/screen2.jpg)




![Возрастание синуса на отрезке [−π/2; π/2]. Функция синус на отрезке [−π/2; π/2] возрастает. Докажем это. Пусть х1, х2 (−π/2; π/2) и х1 0. sinx2 – sinx1= Возрастание синуса на отрезке [−π/2; π/2]. Функция синус на отрезке [−π/2; π/2] возрастает. Докажем это. Пусть х1, х2 (−π/2; π/2) и х1 0. sinx2 – sinx1=](https://prezentacii.org/upload/cloud/19/04/142715/images/thumbs/screen7.jpg)

![Сложим 0. Получим Следовательно, синус этого числа > 0. Доказали, что синус возрастает на отрезке [−π/2; π/2] . Сложим 0. Получим Следовательно, синус этого числа > 0. Доказали, что синус возрастает на отрезке [−π/2; π/2] .](https://prezentacii.org/upload/cloud/19/04/142715/images/thumbs/screen9.jpg)
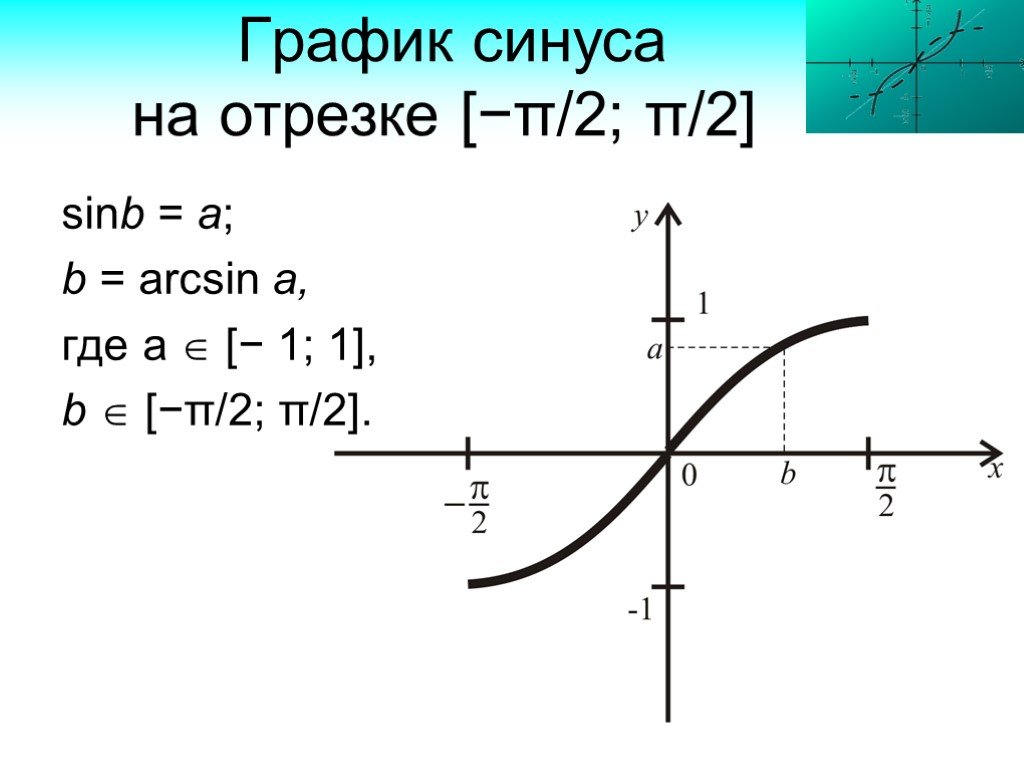
![Определение арксинуса числа. Функция синус принимает значения из отрезка [− 1; 1]. Рассмотрим уравнение sinx = a, где | a | ≤ 1. По теореме о корне уравнение sinx = a имеет один корень b из отрезка [−π/2; π/2] такой, что sinb = a. Это число b называется арксинусом числа а. Обозначают arcsin a. Определение арксинуса числа. Функция синус принимает значения из отрезка [− 1; 1]. Рассмотрим уравнение sinx = a, где | a | ≤ 1. По теореме о корне уравнение sinx = a имеет один корень b из отрезка [−π/2; π/2] такой, что sinb = a. Это число b называется арксинусом числа а. Обозначают arcsin a.](https://prezentacii.org/upload/cloud/19/04/142715/images/thumbs/screen10.jpg)
![Арксинусом числа а из отрезка [− 1; 1] называется такое число из отрезка [−π/2; π/2], синус которого равен а. Арксинусом числа а из отрезка [− 1; 1] называется такое число из отрезка [−π/2; π/2], синус которого равен а.](https://prezentacii.org/upload/cloud/19/04/142715/images/thumbs/screen11.jpg)
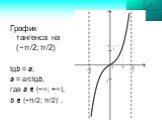
![График синуса на отрезке [−π/2; π/2]. sinb = a; b = arcsin a, где а [− 1; 1], b [−π/2; π/2]. График синуса на отрезке [−π/2; π/2]. sinb = a; b = arcsin a, где а [− 1; 1], b [−π/2; π/2].](https://prezentacii.org/upload/cloud/19/04/142715/images/thumbs/screen12.jpg)


![Определение арккосинуса числа. Функция косинус убывает на отрезке [ 0; π]. (доказательство аналогично). Рассмотрим уравнение cosx = a, где | a | ≤ 1. По теореме о корне это уравнение имеет один корень b из отрезка [ 0; π] такой, что cosb = a. Определение арккосинуса числа. Функция косинус убывает на отрезке [ 0; π]. (доказательство аналогично). Рассмотрим уравнение cosx = a, где | a | ≤ 1. По теореме о корне это уравнение имеет один корень b из отрезка [ 0; π] такой, что cosb = a.](https://prezentacii.org/upload/cloud/19/04/142715/images/thumbs/screen15.jpg)
![Это число называется арккосинусом числа а. Обозначают arccos a. Арккосинусом числа а из отрезка [− 1; 1] называется такое число из отрезка [ 0; π], косинус которого равен а. Это число называется арккосинусом числа а. Обозначают arccos a. Арккосинусом числа а из отрезка [− 1; 1] называется такое число из отрезка [ 0; π], косинус которого равен а.](https://prezentacii.org/upload/cloud/19/04/142715/images/thumbs/screen16.jpg)
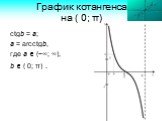
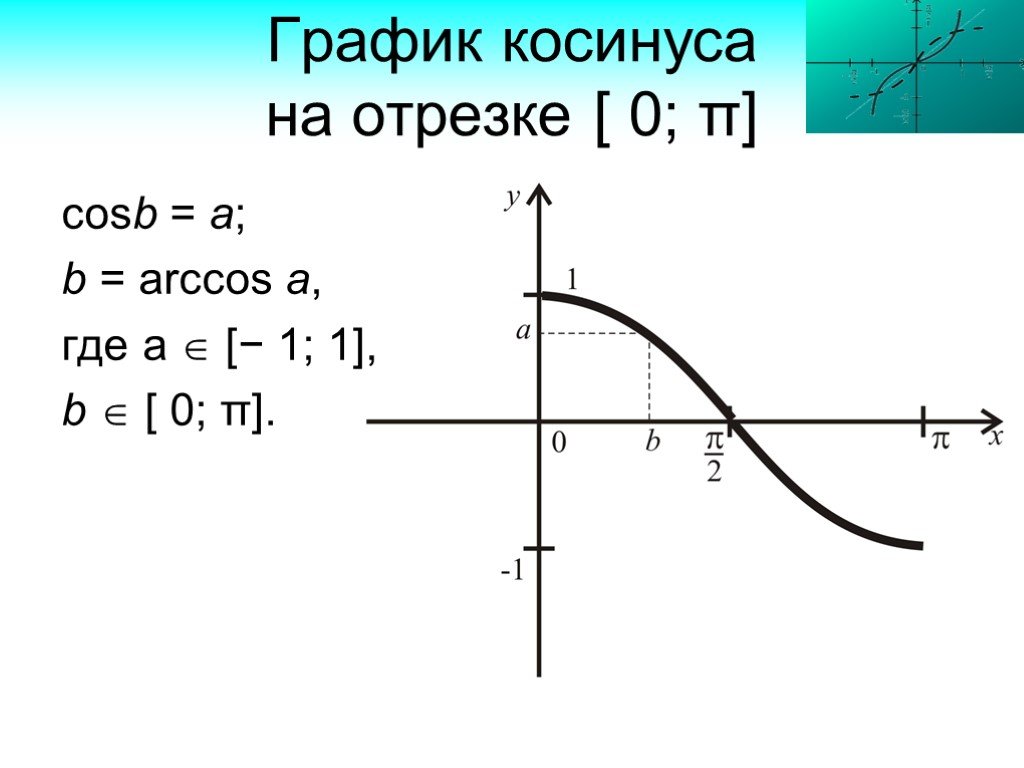
![График косинуса на отрезке [ 0; π]. cosb = a; b = arccos a, где а [− 1; 1], b [ 0; π]. График косинуса на отрезке [ 0; π]. cosb = a; b = arccos a, где а [− 1; 1], b [ 0; π].](https://prezentacii.org/upload/cloud/19/04/142715/images/thumbs/screen17.jpg)