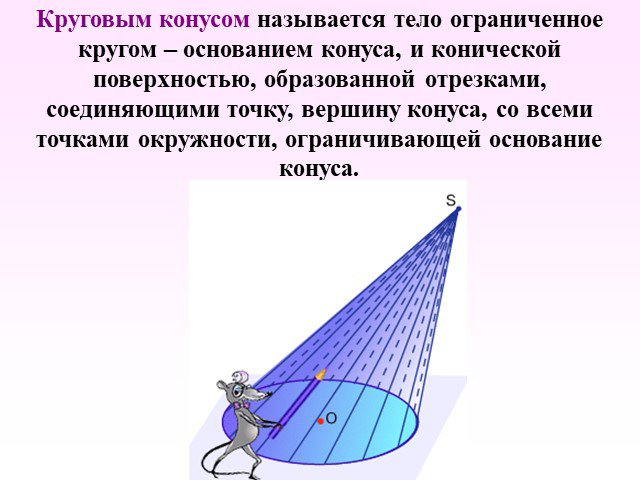
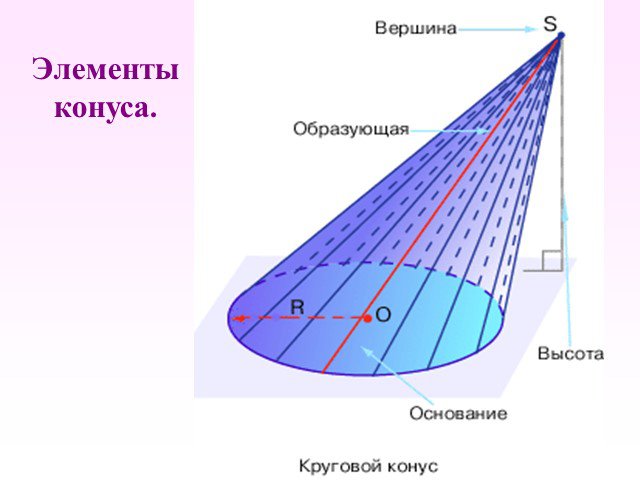
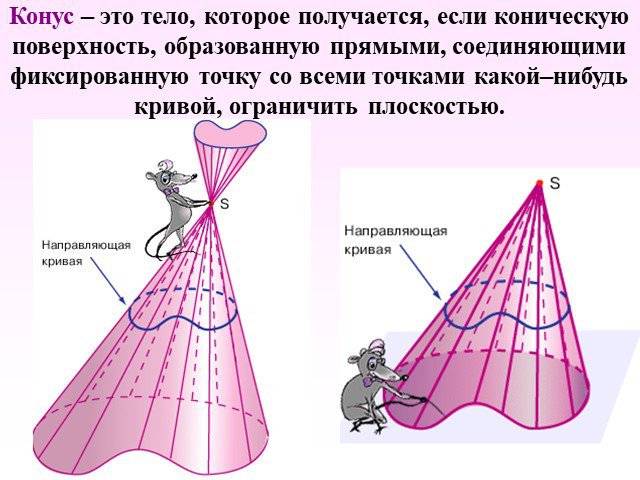
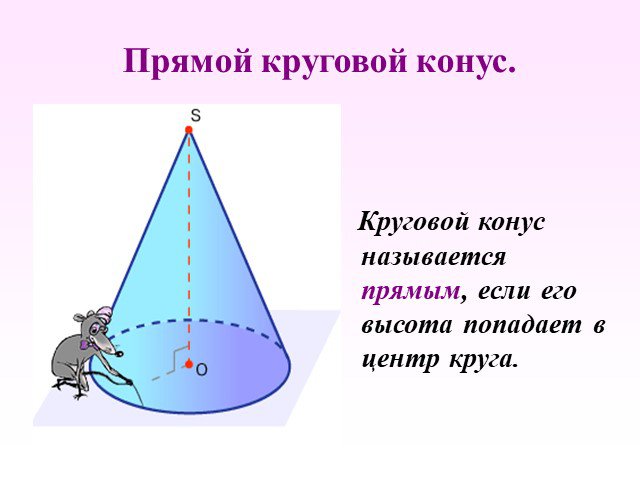
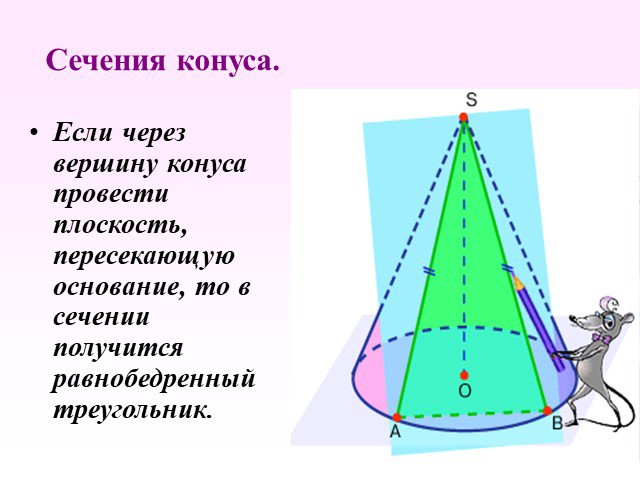
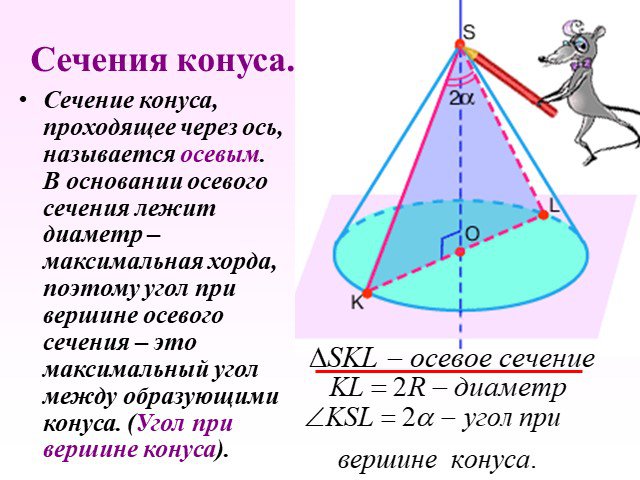
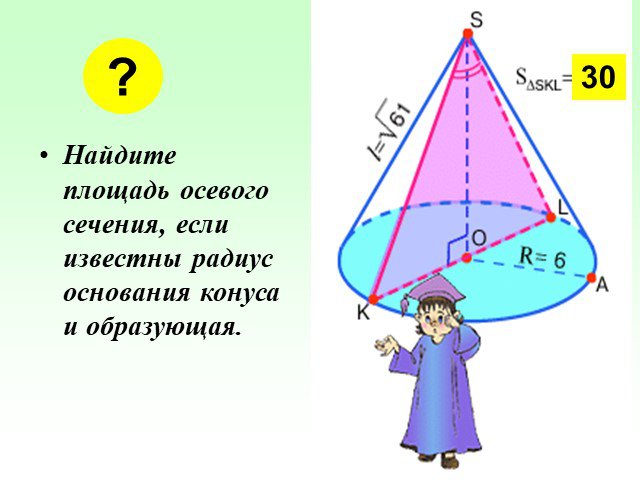
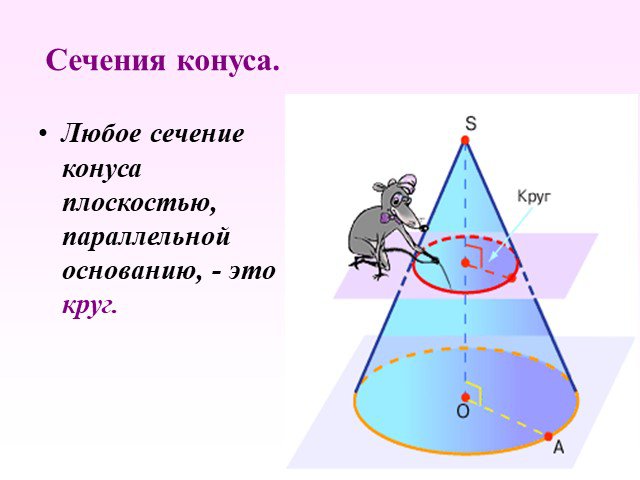
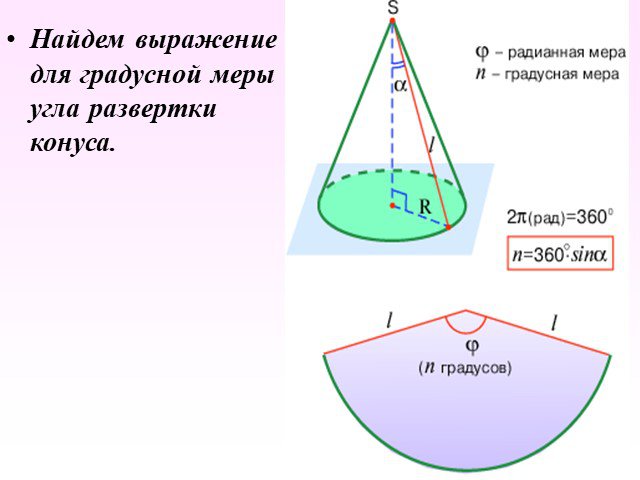
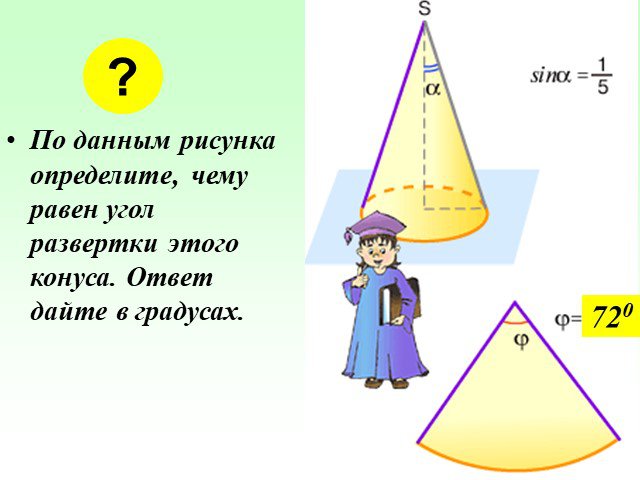
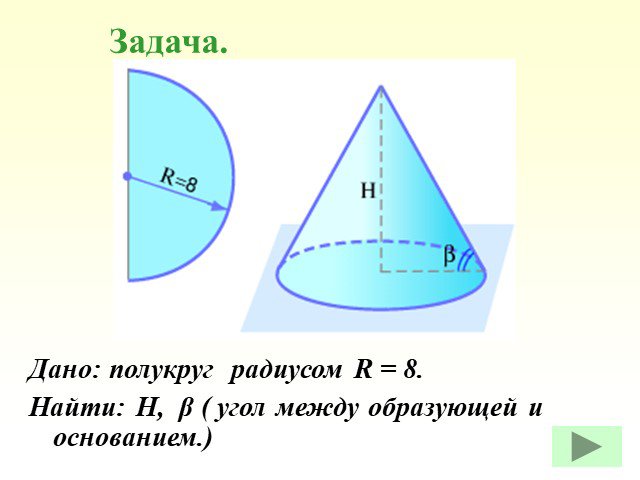
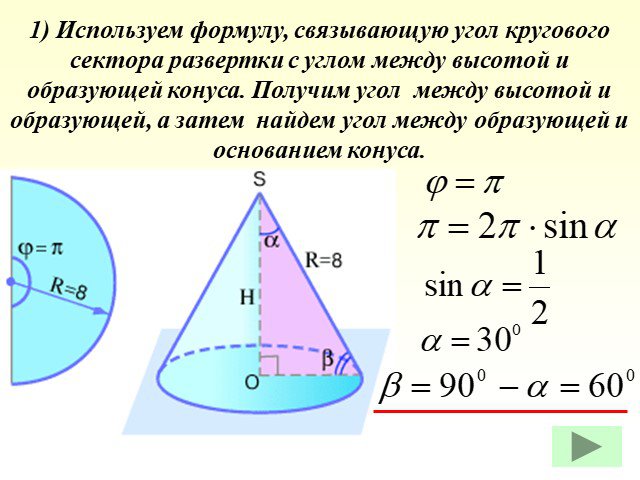
Презентация "Определение конуса" по математике – проект, доклад
Презентацию на тему "Определение конуса" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 42 слайд(ов).
Слайды презентации
Список похожих презентаций
Определение параллельных прямых
ЦЕЛИ УРОКА:. Ввести понятие параллельных прямых; Секущей прямой; Накрест лежащих углов; Односторонних углов; Соответственных углов; Научится определять ...Определение первообразной
Определение первообразной. Цели урока: Повторить правила дифференцирования; Ввести определение первообразной; Научить учащихся применять определение ...Ряды. Определение и свойства
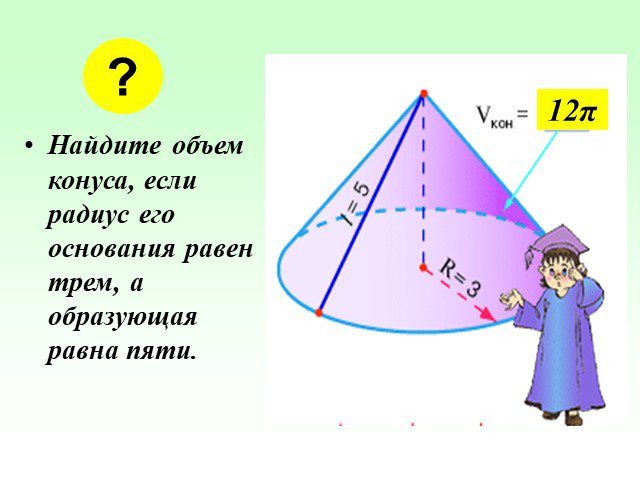
Определение числового ряда. Рассмотрим некоторую числовую последовательность . Составим из членов этой последовательности бесконечную сумму Выражение ...Объем конуса
План урока:. Организационный момент. Повторение основных сведений о конусе. Историческая справка. Объяснение нового материала. Решение задач на объем ...Определение степени с натуральным показателем
Тема: Определение степени с натуральным показателем. Цели: • • Закрепить умение вычислять степень числа, умение выполнять вычисления, зная порядок ...Определение арифметического корня п-ой степени
Повторение:. 1) Имеет ли смысл выражение:. ? 2) Докажите, что:. Число 5 есть корень третьей степени из 125. т. к. Число 0 есть корень восьмой степени ...Определение синуса, косинуса, тангенса и котангенса
Цели урока:. 1.Знать определение синуса, косинуса, тангенса и котангенса. 2.Уметь применять эти определения к решению примеров и задач. 3.Привитие ...Объём цилиндра и конуса
«Не стыдись спросить – не знать еще стыднее!» Японская пословица. В игре участвуют 2 команды. Капитан команды выбирает номер задания, и команда приступает ...Объём цилиндра и конуса задачи практического содержания
№ 1 1 вариант. Выполните рисунок цилиндра, обозначьте на рисунке радиус, высоту. 2 вариант. Выполните рисунок конуса, обозначьте на рисунке образующую, ...Объем конуса цилиндра
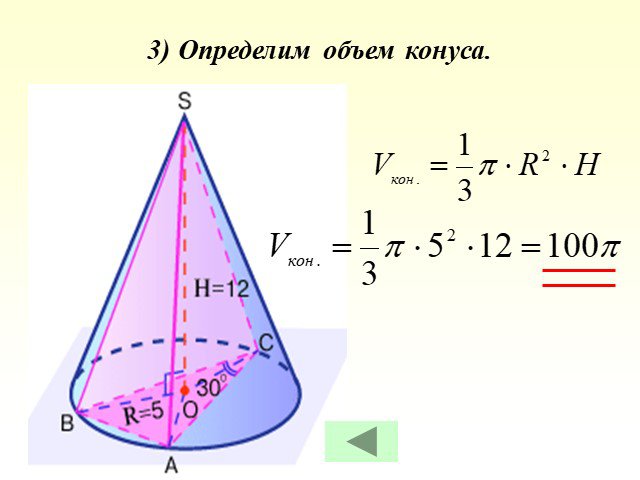
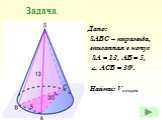
Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 300. В ответе укажите . А О 1 Просят найти. Во сколько ...Объем конуса
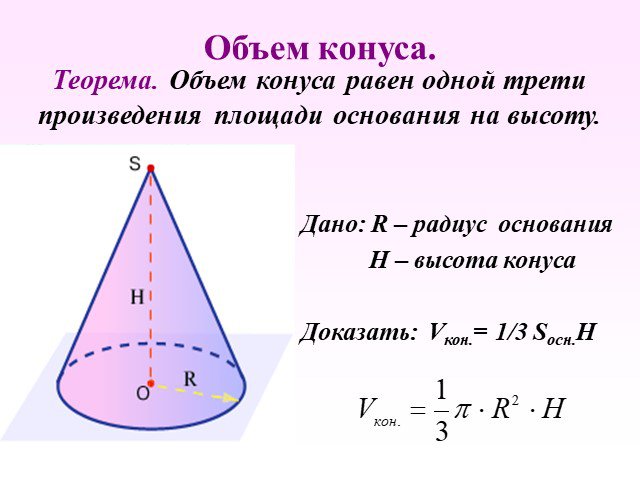
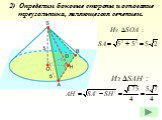
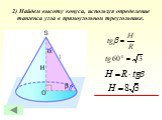
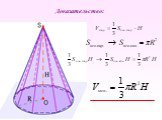
Работу выполнили Ученицы 11 класса МОУ «Тугустемирская СОШ» Кудряшова Наташа Дусаева Гульнара. Теорема. Объем конуса равен одной трети произведения ...Объём конуса
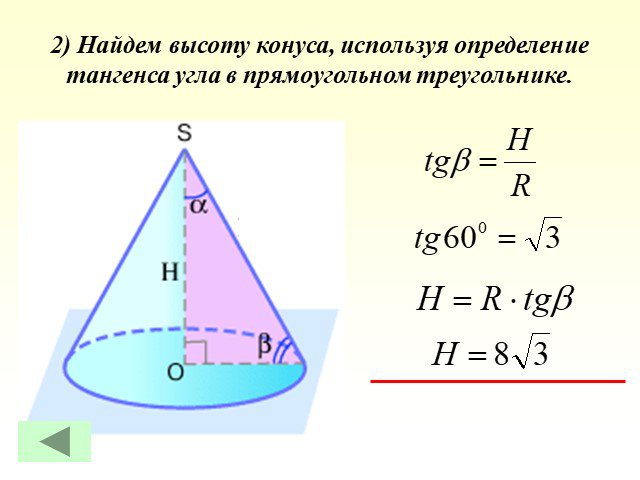
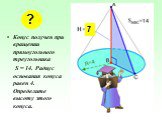
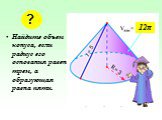
1. Высота конуса равна 8 см. На каком расстоянии от вершины конуса надо провести плоскость, параллельную основанию, чтобы площадь сечения была равна ...Определение подобных треугольников
Немного о себе. Привет всем меня зовут Алеся мне 15 лет учусь в №11 школе в 8 «Г» классе. Я занимаюсь в клубе самодеятельной песни. Мой клуб называется ...Определение арифметической прогрессии
. . ФОРМУЛА n-го члена арифметической прогрессии. . Устная работа № 16.1 № 16.2 № 16.3. . Информационные источники:. Мордкович А.Г., Семёнов П.В. ...Определение производной
Производной функции y=f(x) называется предел отношения приращения функции к приращению независимого аргумента, когда приращение аргумента стремится ...Определение вероятности
При классическом определении вероятность события определяется равенством Р(А) = m/n, где m – число элементарных исходов испытания, благоприятствующих ...Определение степени с натуральным показателем
«Веселые старты» среди 1-2 классов. «Веселые старты» среди 3-4 классы. Шахматы среди 5-х классов. Настольный теннис среди 6-7 классов. Баскетбол среди ...Определение геометрической прогрессии
ЦЕЛЬ УРОКА :. Формирование понятия геометрической прогрессии, используя сопоставление и противопоставления понятию арифметической прогрессии. Познакомить ...Определение угла
Класс: 7 «А» Дата: ноябрь 2010 года Предмет: геометрия Тип урока: объяснение нового материала Тема урока: «Первые уроки геометрии. Углы» Форма урока: ...Конспекты
Определение подобных треугольников
Урок по геометрии в 8 классе. «Определение подобных треугольников». Цель. 1. Ввести новые понятия: отношение отрезков, пропорциональные отрезки, ...Определение степени с натуральным показателем
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа №13». муниципального образования г. Братска. ...Объемы цилиндра конуса
Объемы цилиндра конуса. Цель: совершенствовать навыки решения задач на нахождение объемов фигур. . вращения (цилиндра и конуса). Задачи: -способствовать ...Определение подобных треугольников
Леонова Людмила Михайловна. (. люда20. ). учитель математикиГБОУ лицей № 265 г. Санкт-Петербурга. Урок по геометрии в 8 классе по учебнику Л. ...Определение числовой функции. Виды. Свойства, графики числовых функций. Способы задания функции
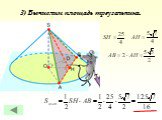
Кейс технологии. Урок алгебры. . Калинина Ирина Борисовна. учитель математики. МАОУ ГИМНАЗИЯ №8 г. Перми. РАЗРАБОТКА УРОКА. c. применением ...Площадь боковой поверхности цилиндра и конуса
Конспект урока по математике. Данные о преподавателе:. Кочерягина Галина Владимировна,. I. квалификационная категория,. . государственное ...Определение геометрической прогрессии. Формула п-го члена геометрической прогрессии
Тема урока:. «Определение геометрической прогрессии. Формула п-го члена геометрической прогрессии». . Класс:9б. . Дата урока:10.02.2014. ...Определение четырёхугольника
Тема урока: Определение четырёхугольника. Цели:. Образовательная –. ввести понятие о четырёхугольнике и его элементах, научить отличать выпуклый ...Определение вероятности
Автор: Волобуева Лидия Ивановна. Место работы: РС(Я), Алданский район, МБОУ «Средняя общеобразовательная школа № 4 пос. Нижний Куранах». Тема: ...Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии
Тема урока:. . Определение геометрической прогрессии. Формула n. -го члена геометрической прогрессии. Тип урока. :. изучение нового материала. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:25 апреля 2015
Категория:Математика
Содержит:42 слайд(ов)
Поделись с друзьями:
Скачать презентацию