Конспект урока «Определение подобных треугольников» по геометрии для 8 класса
Леонова Людмила Михайловна (люда20)
учитель математики
ГБОУ лицей № 265 г. Санкт-Петербурга
Урок по геометрии в 8 классе по учебнику Л. С. Атанасяна.
Тема. Определение подобных треугольников.
Цель. 1. Ввести новые понятия: отношение отрезков, пропорциональные отрезки, сходственные стороны, подобные треугольники, коэффициент подобия.
2. Учить использовать новые понятия, а также известные определения и теоремы для решения задач.
3. Развивать логическое мышление.
Ход урока.
① Повторение ранее изученных понятий. ( Повторить понятия было задано на дом).
-
Что называют отношением чисел? (Это частное от деления двух чисел, которое показывает, во сколько раз одно число больше другого, или, какую часть одно число составляет от другого)
-
Что называют пропорцией? (Равенство двух отношений)
-
В чем заключается основное свойство пропорции? (Произведение крайних членов пропорции равно произведению ее средних членов)
② Проверка решения задач, подготавливающих введение новых понятий. (Задачи были заданы на дом)
Задача №1.
Длина прямой тропинки на дачном участке, ведущей от дома к сараю, составляет 12 м, а тропинки, ведущей к колодцу, составляет 15 м.
-
Найти отношение первой длины ко второй.
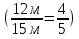 . Что показывает данная величина? ( Показывает, какую часть составляет первая величина от второй).
. Что показывает данная величина? ( Показывает, какую часть составляет первая величина от второй). -
Найти отношение второй длины к первой.
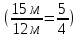 . Что показывает данная величина? ( Показывает, во сколько раз вторая величина больше первой).
. Что показывает данная величина? ( Показывает, во сколько раз вторая величина больше первой). -
Выразить величины в сантиметрах и снова найти отношения. (
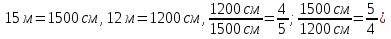 .
. -
Выразить величины в километрах и найти отношения.
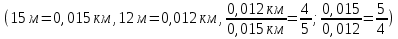 .
. -
Сделать вывод о том, зависит ли отношение длин отрезков от того, в каких единицах они выражены. (Не зависит).
Задача №2.
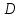
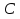
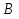
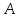
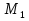
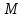
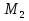
Найти отношение отрезков:
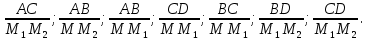
Выбрать равные отношения и записать их равенство.
Решение:
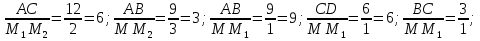
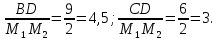
③ Самостоятельная работа с текстом и закрепление новых знаний.
-
Работа с текстом пункта 56 «Пропорциональные отрезки» из §1 ( учебник Л. С. Атанасяна). Прочесть текст, выбрать, сформулировать и записать определения следующих понятий.
-
Отношение отрезков. (Отношением отрезков АВ и СD называется отношение их длин, то есть
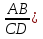 .
. -
Пропорциональные отрезки. (Отрезки АВ и СD пропорциональны отрезкам
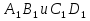 , если
, если 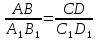 . Отрезки
. Отрезки 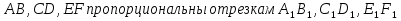 , если справедливо равенство
, если справедливо равенство 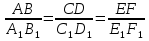 .
.
-
Закрепление новых знаний.
-
№533 (устно). Найти отношение отрезков AB и CD, если их длины равны соответственно 15 см и 20 см. Изменится ли это отношение, если длины отрезков выразить в миллиметрах? (Отношение равно
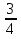 ; при изменении единиц длины оно не меняется)
; при изменении единиц длины оно не меняется) -
№534 (устно, использовать результаты решения домашней задачи №2). Пропорциональны ли изображенные на рисунке отрезки: а)
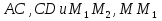 ; б)
; б)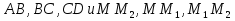 ; в)
; в)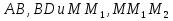 ? (рисунок к домашней задаче №2, раздел ②) – в случаях (а) и (б) пропорциональны, в случае (в) – нет.
? (рисунок к домашней задаче №2, раздел ②) – в случаях (а) и (б) пропорциональны, в случае (в) – нет.
④ Определение подобных треугольников. (Презентация)
-
Слайд с заголовком «Определение подобных треугольников».
-
Слайд с подзаголовком «Понятие сходственных сторон».
-
Демонстрация двух треугольников, у которых углы соответственно равны.
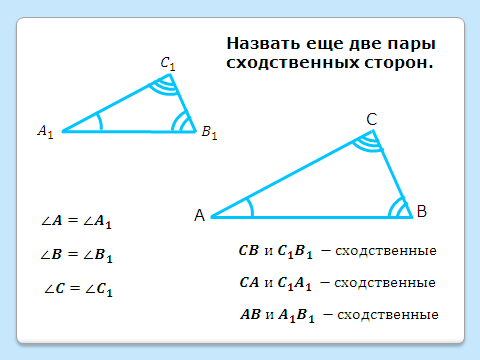
Первоначально на рисунке изображены два треугольника.
Анимация помогает увидеть соответственно равные углы.
Затем выделяется пара равных углов: 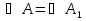 , а вслед за этим появляется пара сторон, лежащих против этих углов:
, а вслед за этим появляется пара сторон, лежащих против этих углов: 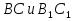 ; вводится их название – сходственные стороны.
; вводится их название – сходственные стороны.
Для закрепления понимания предлагается назвать еще две пары сходственных сторон, после чего появляется соответствующая запись: 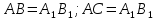 .
.
-
Слайд с подзаголовком «Определение подобных треугольников».
-
Демонстрация двух треугольников:
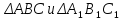 , у которых отмечены соответственно равные углы, а рядом – запись «Треугольники
, у которых отмечены соответственно равные углы, а рядом – запись «Треугольники 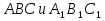 называются подобными, если…»
называются подобными, если…»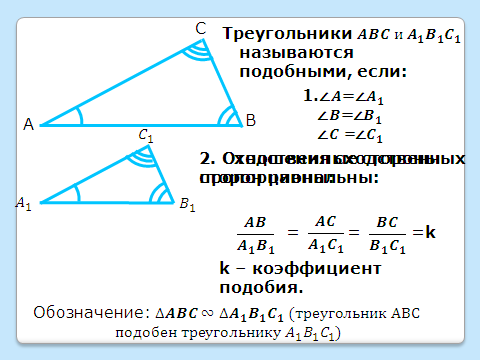
Анимация: Появляется запись «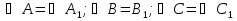 .»
.»
Анимация: Появляется запись «Отношения сходственных сторон…»
Задание ученикам: Назвать отношения сходственных сторон.
С помощью анимации появляется запись, выражающая отношения сходственных сторон: 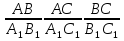 .
.
Далее к записи «Отношения сходственных сторон» добавляется слово «равны» и между отношениями появляются знаки равенства.
Затем ученики должны ответить на вопрос: «Что означает равенство отношений для отрезков 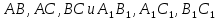 ?»
?»
Следующим шагом запись «Отношения сходственных сторон равны» заменяется записью «Сходственные стороны пропорциональны»
Затем вводится число k для обозначения равных отношений, его название – коэффициент подобия, появляются соответствующие записи на слайде.
Последним шагом вводится обозначение подобных треугольников: 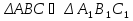 .
.
⑤ Решение задач.
№541.Подобны ли треугольники 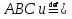 , если
, если 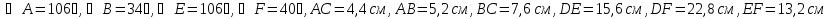 ?
?
| Решение:
B A C D F E Получили: ∠A=∠E; ∠B=∠D; ∠C=∠F
Вывод: ΔABC∾ΔEDF. |
⑥ Домашнее задание.
§1(п. 56, п. 57) – знать смысл понятий
-
Отношение отрезков.
-
Пропорциональные отрезки.
-
Сходственные стороны у треугольников.
-
Подобные треугольники.
-
Коэффициент подобия.
№542 (решить)
№535 (разобрать и записать доказательство, разбив его на пункты)
Решение задач.
№542.
| Решение:
АВ и КМ – сходственные, значит ∠С=∠N. ВС и МN – сходственные, значит ∠А=∠К. 2)Получаем следующий чертеж М К N В А С 3)
|
Ответ: KN=14,7 см; KM=8,4 см; MN=10,5 см.
№535.
Дано:
ΔАВС;
AD – биссектриса
Доказать:
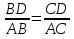
С
D
В
А
H
Чертеж:
Доказательство:
-
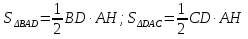 ;
; 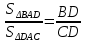 .
. -
Так как ∠BAD=∠DAC, то по теореме об отношении площадей треугольников, имеющих соответственно равные углы
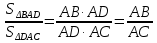 .
. -
Учитывая пункты 1 и 2, получаем
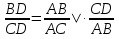
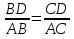
Вывод. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.
Здесь представлен конспект к уроку на тему «Определение подобных треугольников», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Геометрия (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

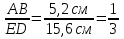
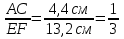
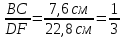
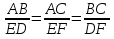 , то Δ
, то Δ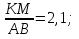

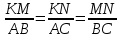 (так как Δ
(так как Δ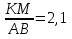 . Тогда
. Тогда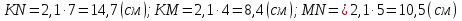 .
.