Презентация "Экстремум функции" по математике – проект, доклад
Презентацию на тему "Экстремум функции" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 29 слайд(ов).
Слайды презентации
Список похожих презентаций
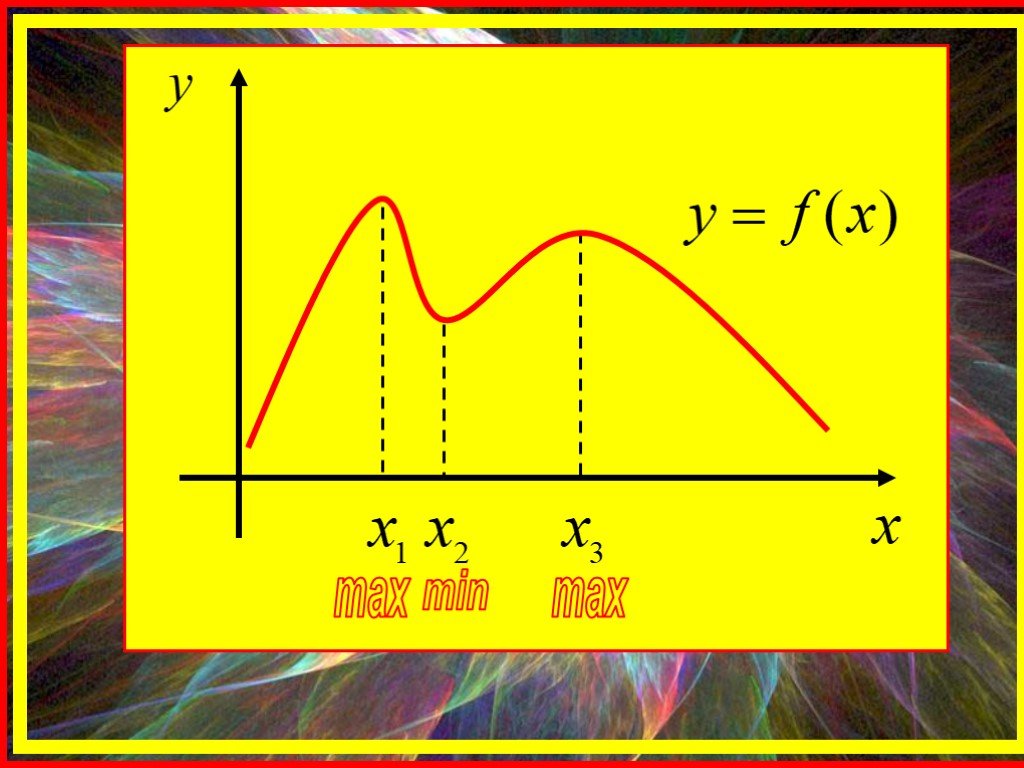
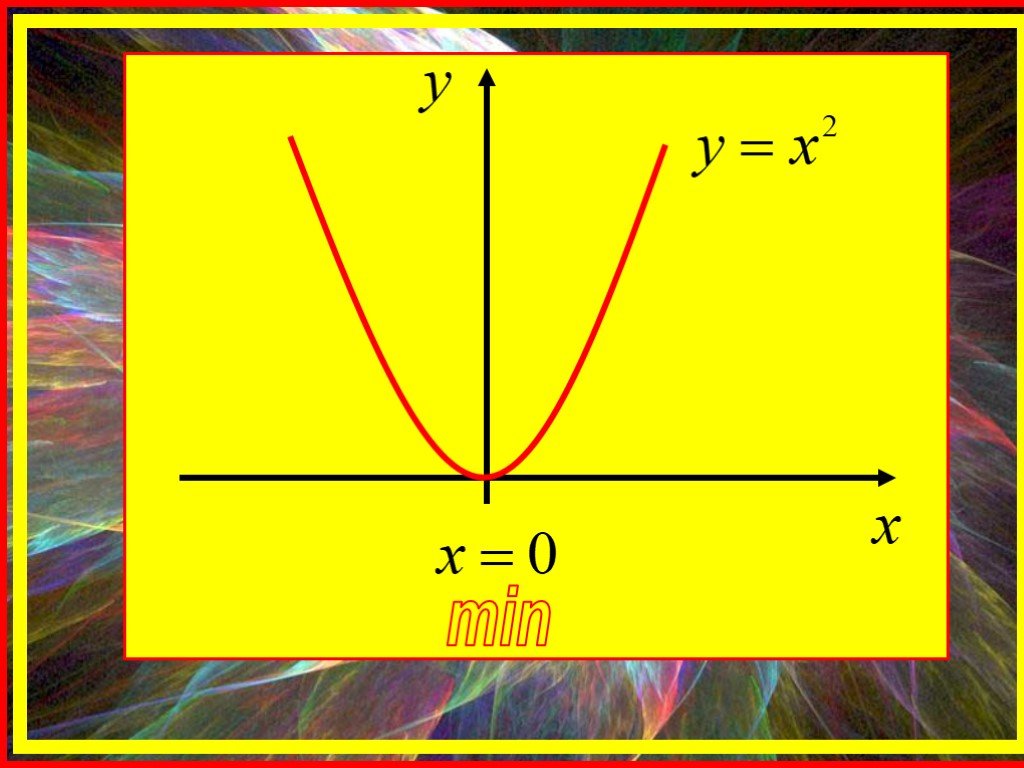
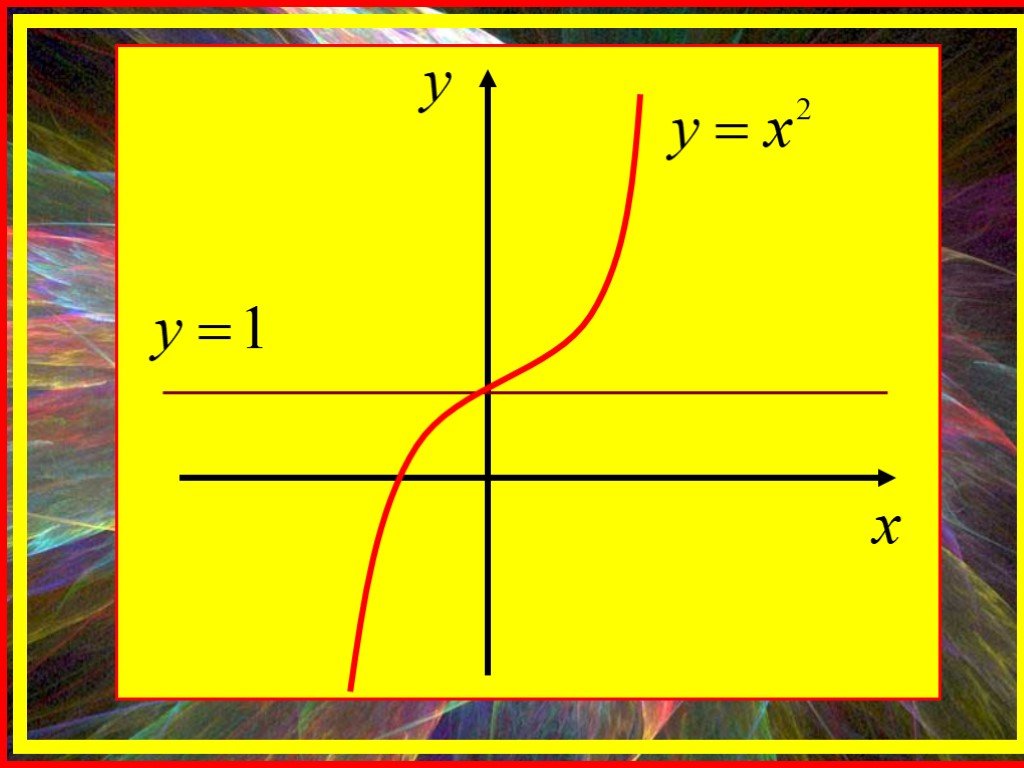
Экстремум функции
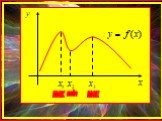
Зависимость давления газа от объёма. P=f(v) P 0 V. Зависимость силы тока от напряжения. I=f(u) I u. Изменение силы тока при размыкании цепи. I=f(t) ...Экстремумы функции
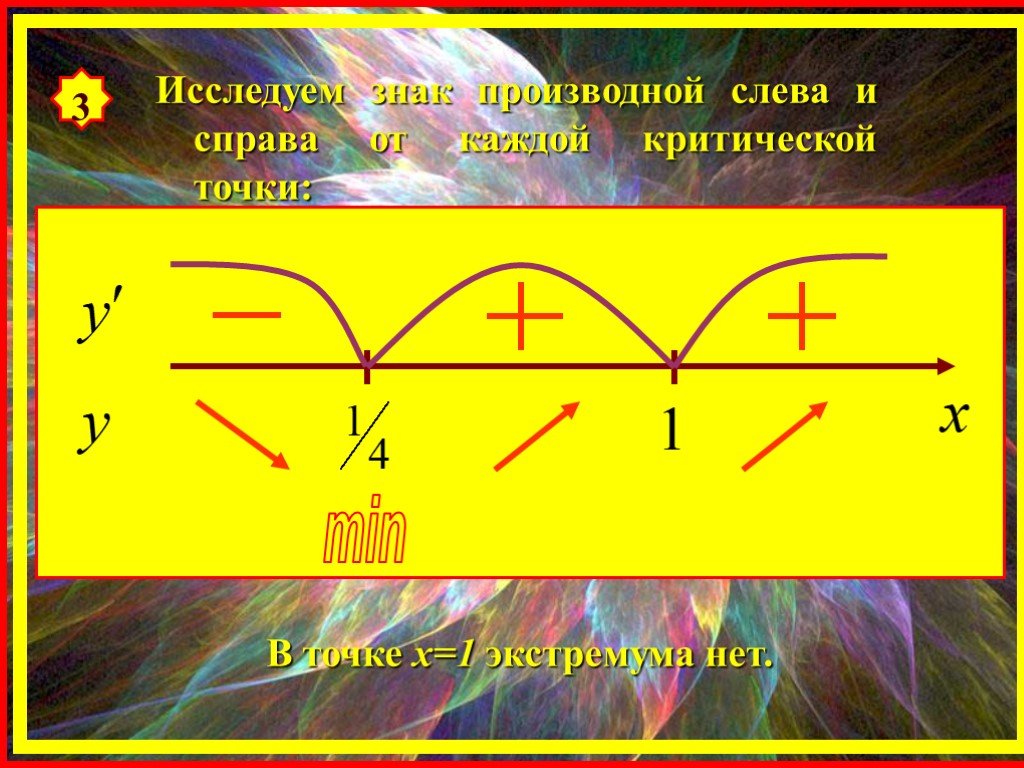
a Пример x y 0 b. Найдите точку минимума функции y = x3 – 48x + 17.1) y / = 3x2 – 48.
2) y / = 3x2 – 48 = 3(x2 – 16) = 3(x – 4)(x + 4).
Выполнение ...
Применение производной для исследования функции на монотонность и экстремумы
Х У 0 касательная α. k – угловой коэффициент прямой (касательной). Геометрический смысл производной: если к графику функции y = f(x) в точке с абсциссой ...Уравнение касательной и нормали к графику функции
Уравнение касательной и нормали к графику функции. 10 класс Физико-математический профиль. Учитель Ласкевич С.В. Цель урока: 1)узнать как составлять ...Тригонометрические функции и их свойства
Системы счисления. Память человечества не сохранила, не донесла до нас имя изобретателя колеса или гончарного круга. Это и не удивительно: более 10 ...Свойства функции у = tg х и ее график
Цели урока:. повторить раннее изученные свойства функции у=tgx; научиться строить график функции у=tgx, используя данные свойства функции. на основе ...Свойства и график функции синус
Устная разминка 1 3 4 5 6 7 8 9 10 11 13 14 15 ☺ cos90° sin90° sin(π/4) cos180° sin270° sin(π/3) cos(π/6) cos360° ctg(π/6) tg(π/4) sin(3π/2) cos(2π) ...Производная функции
Задание № 1. 1. На рисунке изображен график функции y=f(x) и касательная к нему в точке с абсциссой х0 Найдите значение производной в точке х0 1) ...Применение производной функции
с и л а. в у м е. I вариант II вариант Буква С Буква В. Буква И Буква У. Буква Л Буква М. Буква А Буква Е 7. Сложилась фраза. ...Предел функции в точке
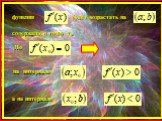
Одна и та же кривая, три разные функции. Отличие – поведение в точке х = а. f(a) – не существует, т.к. в точке х =а функция у = f(х) не определена. ...Возрастание и убывание функции
Числовые промежутки. [α;b] – отрезок (α;b) – интервал (α;b] – полуинтервал [α;b) - полуинтервал. Функция f(x) называется возрастающей на некотором ...Влияние коэффициентов а, b и с на расположение графика квадратной функции
Определите, график какой функции изображен на рисунке:. у = х² – 2х – 1; у = –2х² – 8х; у = х² – 4х – 1; у = 2х² + 8х + 7; у = 2х² – 1. у = ½х² – ...Взаимное расположение графиков линейной функции
Разбейте функции, заданные формулами, на группы:. у = 2х - 3; у = х2 - 3; у = - 5х; у = 4 - 0,5х; у = - х +2; у=15х;. 7. 8. 9. 10. у = х (1 - х). ...Взаимно обратные функции
Задача. у = f (x), x - ! Найти значение у при заданном значении х. Задача. у = f (x), у- ! Найти значение х при заданном значении у. Дано: у = 2х ...Взаимно обратные функции
Цель проекта: Изучить поведение взаимно обратных функций. Установить связь графиков прямой и обратной функций. Подготовиться к успешной сдаче ЕГЭ. ...Алгоритмы построения графиков функции
График функции у = |х| а) Если х≥0, то |х| = х функция у = х, т.е. график совпадает с биссектрисой первого координатного угла. б) Если х. Построить ...Чётные и нечётные функции
Определение.Функция y=f (x) называется чётной, если: D (f) симметрична относительно нуля; 2) для любого х Є D (f) верно равенство: f (-x) = f (x). ...
Построение графика функции методом ее исследования с помощью производной
доцент кафедры математического образования Батан Любовь Федоровна. учитель математики первой квалификационной категории МОУ лицей № 176 Ткаченко Зоя ...Вычисление производной функции
При вычислении производной функции, будем иметь в виду, что один из способов найти производную - это взять достаточно малые значения справа и слева ...Преобразования графиков квадратичной функции
Квадратичной функцией называется функция вида у = ax²±bx±c Например : у=2x²+3x-4, а=2, b=3,c=-4 Графиком квадратичной функции является парабола Для ...Конспекты
Производная показательной функции
Конспект урока по теме «Производная показательной функции» в 11 классе. Цель:. Ввести понятие «экспоненты», «натурального логарифма», сформировать ...Производная функции
Производная функции. Обобщающий урок в 10 классе. Т.М. РЕВЯКИНА,. . учитель математики ШЛ №101. Девиз урока:. Решай, ищи, твори и мысли. ...Применение параллельного переноса при построении квадратичной функции
Урок по теме. : «Применение параллельного переноса при построении квадратичной функции». Тип урок. а: урок повторения. Цель урока:. Повторить ...Применение производной к исследованию функции
Урок 49. Тема урока:. «Применение производной к исследованию функции». Предмет:. Алгебра и начала анализа. Тип занятия:. закрепления изученного ...Экстремум функций двух переменных. Наибольшее и наименьшее значения
Тема: Экстремум функций двух переменных. . . Наибольшее и наименьшее значения. Цель занятия:. . закрепление знаний полученных на лекциях ...Предел функции в точке, свойства. Бесконечно большие и бесконечно малые функции. Непрерывность функции
Министерство образования и науки Самарской области. . ГБОУ СПО «Безенчукский аграрный техникум». Конспект занятия. ТЕМА. Предел функции ...График линейной функции
КОНСПЕКТ УРОКА для 7 класса«График линейной функции». (Тема урока). . ФИО (полностью). . Колесникова Людмила Александровна. . . ...Функции. Тригонометрические функции
Учитель математики ГБОУ СОШ № 230 с углубленным изучением химии и биологии. Ваганова Г. В. Тема. :. . « Функции. Тригонометрические ...График квадратичной функции
МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 17. КУРГАНИНСКИЙ РАЙОН. Тема: «График квадратичной функции». ...График квадратичной функции и модуль
Администрация города Улан - Удэ. Комитет по образованию. МАОУ «Средняя общеобразовательная школа № 25». Урок алгебры в 9 классе. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:12 марта 2019
Категория:Математика
Содержит:29 слайд(ов)
Поделись с друзьями:
Скачать презентацию