Конспект урока «Экстремум функций двух переменных. Наибольшее и наименьшее значения» по математике

Тема: Экстремум функций двух переменных.

Наибольшее и наименьшее значения.

Цель занятия:

• закрепление знаний полученных на лекциях и применение их на практике;

• научить исследовать функцию нескольких переменных на максимум и минимум с использованием производных высших порядков;

• вывести алгоритм нахождения наименьшего и наибольшего значений функции;
  решать задачи на отыскание наибольших и наименьших значений функции;

• развитие пространственного мышления, умение планировать, мыслить логически и по аналогии.

Методы: словесные, по характеру познавательной деятельности – проблемные, по дидактической цели – познавательные.

Ход занятия.

1. Организационная часть. Студенты записывают тему занятия.

2. Актуализация опорных знаний. В начале занятия проводится небольшая по времени (10-15 минут) фронтальная работа, которая позволяет актуализировать базовые знания студента.

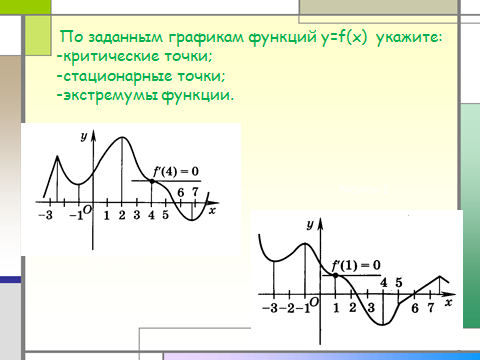
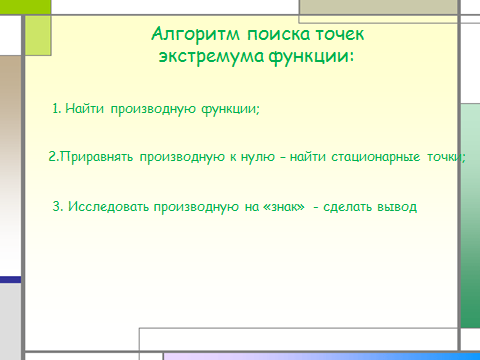
3. Работа по повторению:

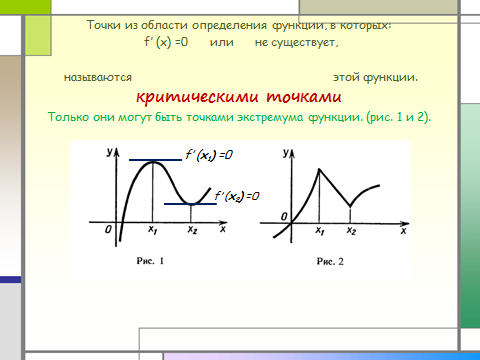
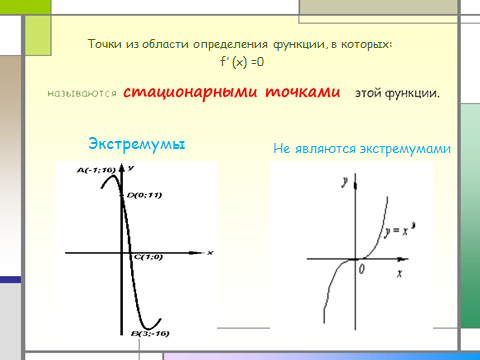
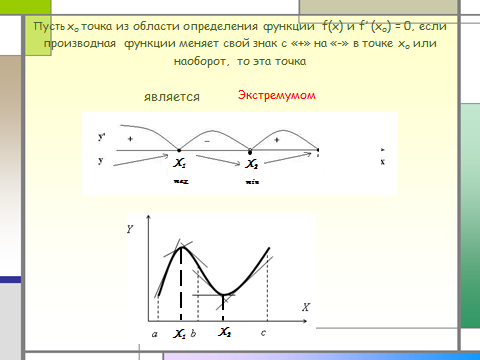
-критические точки;

-стационарные точки;

-экстремумы функции.

4. Выполнение самостоятельной работы:

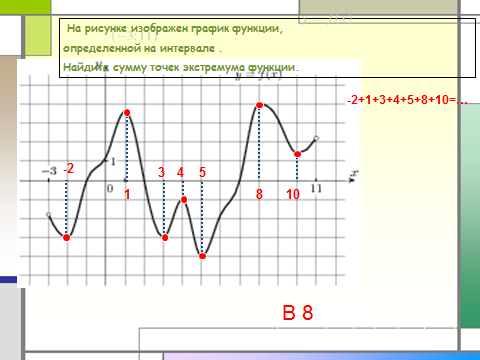
2. Основная часть. Изучение новой темы.

Экстремум функции двух переменных

Рассмотрим пример решения задачи:

Ответы на вопросы. Закрепление полученных знаний.

Нахождение наибольшего и наименьшего значений функции широко применяется при решении многих практических задач на нахождение наилучших, оптимальных решений при наименьших затратах труда, в так называемых задачах на оптимизацию.

ПРИМЕР. Рекламный щит имеет форму прямоугольника S=9 м². Изготовьте щит в виде прямоугольника с наименьшим периметром

Найти наибольшее и наименьшее значение функции у = х³ - 3х² - 45х + 1 на [-4; 6]

без построения графика.

Во время самостоятельной работы сильные студенты вызываются к доске и решают у доски наиболее сложные занятия из домашней работы.

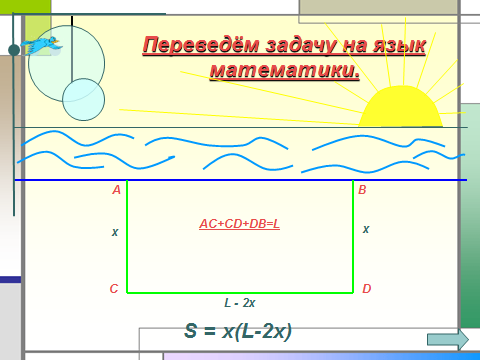
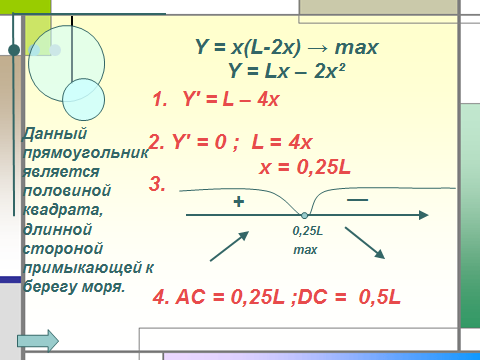
Легенда об основании Карфагена гласит, что когда финикийский корабль пристал к берегу, местные жители согласились продать прибывшим столько земли, сколько можно огородить её одной бычьей шкурой. Но хитрая царица Дидона разрезала эту шкуру на ремешки, связала их и огородила полученным ремнём большой участок земли, примыкавший к побережью.

Вопрос: какую наибольшую площадь земли могли купить финикийцы?

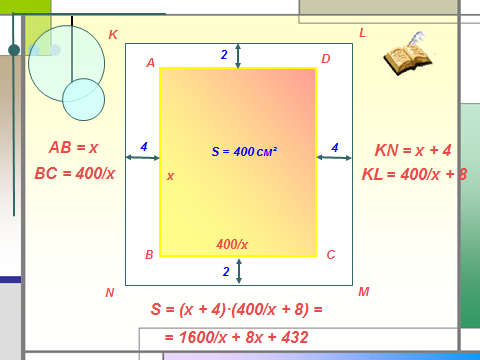
Печатный текст (вместе с промежутками между строками) одной страницы книги должен занимать 400 см². Верхние и нижние поля страницы должны иметь ширину 2 см. Боковые – 4 см.

Вопрос: каковы самые выгодные размеры страницы, исходя только из экономии бумаги?

Следующим этапом изучения темы является подробное решение примера преподавателем. Это позволит студентам последующие примеры решать по аналогии с разобранным, попутно преодолевая трудности с помощью знаний, которыми они уже обладают.

Пример. Исследовать на экстремум функцию

.

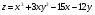Решение

Проверим выполнение необходимого условия существования экстремума функции. В результате чего получим стационарные точки.

Находим частные производные и составляем систему уравнений

;

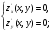
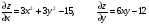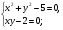
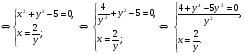
Решим отдельно уравнение 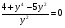. Дробь равна нулю, когда ее числитель равен нулю, т.е. 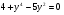. Пусть 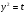, тогда исходное уравнение примет вид квадратного трехчлена 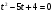. Используя теорему, обратную теорему Виета, получаем корни уравнения .

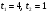Таким образом получаем: 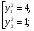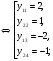подставляя полученные значения в систему получаем четыре стационарные точки:

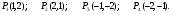
Используя теорему о достаточном условии существования экстремума функции двух переменных, составляем определитель 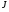и находим точки максимума и минимума.

Найдем производные второго порядка:

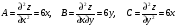и составим определитель

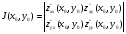
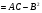для каждой стационарной точки.

1) Для точки

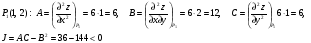
Значит, в точке 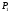экстремума нет.

2)

.

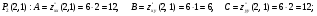
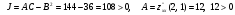В точке 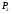, согласно достаточному условию существования экстремума, функция имеет минимум. Минимум этот равен значению функции при .

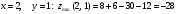3)

.

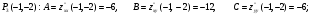
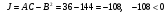Экстремума в точке 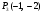нет.

4)

.

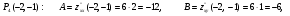
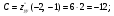
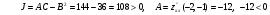В точке 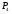функция имеет максимум: .

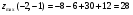V этап: Выполнение самостоятельной работы. (Работы сдаются на проверку учителю)

Найти наибольшее и наименьшее значения функции:

I в. 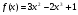на отрезке .

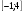II в. 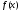= 9x + 3x² – x³ на отрезке [– 2; 2].

По окончании выполнения самостоятельной работы студенты готовятся к ответам на следующие вопросы.

1. Определение экстремума функции двух переменных.

2. Необходимое условии экстремума.

3. Достаточное условие экстремума функции двух переменных.

VI. Рефлексия. Определение домашнего задания.