Конспект урока «СЛОЖЕНИЕ И ВЫЧИТАНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ» по математике для 5 класса






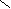

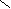
ГБОУ СОШ № 1245 с углубленным изучением иностранного языка (английского) ЮАО г. Москвы
ИГРОВЫЕ ТЕХНОЛОГИИ
УРОК МАТЕМАТИКИ В 5 КЛАССЕ
Учитель Горбунова Наталья Ефимовна
Тема урока: СЛОЖЕНИЕ И ВЫЧИТАНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ
(урок комплексного применения знаний)
Основная цель: Повторить правила и закрепить умения и навыки сложения и вычитания дробей с разными знаменателями, основное свойство дроби.
Процесс игры делает процесс обучения более эффективным, т.к. увлекает пятиклассников, способствует развитию творческой активности, внимания, критического мышления, дает эмоциональный заряд бодрости на весь урок, препятствует усталости. Применение информационных технологий делает урок ярче, нагляднее, экономит время урока. Работа в группе развивает коммуникативные умения и навыки, воспитывает ответственность, заинтересованность в общем результате.
Урок сопровождается мультимедийной презентацией.
«Эти дроби… Ох, эти дроби!
Жизнь, как дробь, и точна, а - мимо,
В ней делитель упрям, неудобен,
А делимое – неделимо».
БОЛЬШОЙ «ДРОБНЫЙ МОЗГОДРОМ» (урок-игра)
Учитель: Вы научились складывать и вычитать дроби с разными знаменателями, и сегодня мы с вами отправляемся на БОЛЬШОЙ «ДРОБНЫЙ МОЗГОДРОМ». Что это такое? Сейчас узнаете! Смелее в путь, к победе над коварными дробями!
Напутствие участникам.
Пускай повсюду ждет тебя успех!
Он любит любознательных и тех,
Кто не боится трудностей,
Кто ценит юмор,
Смекалку и пытливый ум,
Кто мозг свой не бережет от дум!
В задачах тех ищи удачи,
Где получить рискуешь сдачи.
И в математику тропинки
Ты одолеешь без запинки!
Класс делится на 3-4 команды по 5-6 человек. Каждая команда выбирает капитана (это лучше сделать заранее). Жюри – 2 ученика, которых выбирает класс, учитель.
1. Дробная перестрелка» (разминка)
Команды получают конверты с карточками (по 5 примеров на команду). Каждый член команды решает один пример, а капитан располагает ответы на «мишени» в порядке убывания от центра. За верные ответы и верное расположение – 6 баллов, за каждую ошибку снимается 1 балл. Член жюри вписывает полученные баллы в таблицу.

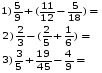
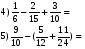
Ответы: 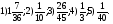
2. Вглубь веков (историческая страничка)
Учитель: Первой дробью, с которой познакомились люди, была половина (1\2), потом появилась 1\3. Египтяне все дроби, кроме 2\3, представляли как суммы долей. Например, 8\15 = 1\3 + 1\5. Вот какая задача была найдена в древнеегипетском папирусе: «Разделить 7 хлебов между 8 людьми». По-египетски задача решалась так: 7\8 = 1\2 + 1\4 +1\8, т.е. каждому человеку надо было дать полхлеба, четверть хлеба и восьмушку хлеба.
В Вавилоне пользовались дробями со знаменателем 60, а в Древнем Риме предпочитали 12-тые доли (унции). Но Римским купцам приходилось делить и на 10, и на 100, и на 1000. Так появились проценты – сотые части (%) и промилли – тысячные части (‰).
Современную систему записи дробей с числителем и знаменателем создали в Индии. Только там писали знаменатель сверху, а числитель – снизу и без дробной черты. А записывать дроби в точности, как сейчас, стали арабы.
В средние века действия над дробями считались самой сложной областью математики. До сих пор немцы говорят про человека, попавшего в затруднительное положение, что он «попал в дроби».
А теперь решите-ка и вы египетскую задачу о разделе хлебов.
Верный ответ – 3 балла.
Задача «О разделе хлебов». Разделите 5 хлебов между 6 людьми, не разрезая ни одного на 6 частей.
Решение задачи: 5\6 = 1\2 + 1\3
3. Превращение дробей (бизнес-задача)
Выберите одну из карточек. На них задания разной сложности, поэтому за них – разное количество баллов. За верное решение эти баллы прибавляются, но за неверное – вычитаются! (Этот конкурс сложный, при дефиците времени его лучше пропустить.)
Какое число надо прибавить к числителю и знаменателю дроби 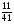 , чтобы она превратилась в
, чтобы она превратилась в 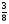 ? (2 балла) Ответ: 7
? (2 балла) Ответ: 7
Какое число надо вычесть из числителя и знаменателя дроби 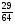 , чтобы она превратилась в
, чтобы она превратилась в 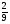 ? (3 балла) Ответ: 19
? (3 балла) Ответ: 19
Какое число надо вычесть из числителя и прибавить к знаменателю дроби 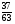 , чтобы она превратилась в
, чтобы она превратилась в 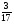 ? (4 балла) Ответ: 22
? (4 балла) Ответ: 22
4. Задача Пифагора
На вопрос о том, сколько у него учеников, древнегреческий математик Пифагор ответил так: «Половина моих учеников изучает математику, четвертая часть изучает природу, седьмая часть проводит время в молчаливом размышлении, а остальную часть составляют 3 девы». Сколько учеников было у Пифагора?
Совет: примите количество учеников сначала за 1.
За верное решение задачи – 5 баллов.
Решение задачи Пифагора:
1) 1\2 + 1\4 + 1\7 = 25\28; 2) 1 – 25\28 = 3\28;
3) 3\28 – это 3 девы, значит, всего учеников было 28.
5. Как Магистр Рассеянных Наук сражался с пиратами
Вот его рассказ: «На корабль напали пираты. Когда я выскочил на палубу, то увидел, что вся команда лежит связанная, кроме штурмана и радиста, которые отчаянно защищаются. Я бросился им на помощь. Первым делом я сосчитал число разбойников, носившихся по палубе, и разделил их на три группы. Штурману досталась половина всех пиратов, радисту – 1\3, а мне – всего 1\4. Но, как говорил фельдмаршал Кутузов, в бою берут не числом, а умением! Не прошло и 10 минут, как мы расправились с пиратами, и сражение было выиграно. Мы развязали всю команду, и тут только обнаружилось, что капитан дизеля исчез! И куда он мог подеваться?»
Помогите Магистру найти капитана.
За верное решение задачи – 4 балла.
Решение: 1\2 + 1\3 + 1\4 = 13\12, но 13\12 1. Капитана связали вместе с пиратами.
6. Конкурс капитанов
Вопросы задаются на слух. Отвечает тот, кто первым поднял руку. За каждый верный ответ команда получает 1 балл.
-
Что получится, если половину разделить на половину? (1)
-
Какое число не может стоять в знаменателе дроби? (0)
-
Назовите дробь, у которой числитель меньше знаменателя, и которая не изменится, если ее запись перевернуть «вверх ногами». (6\9)
-
Как изменится дробь, если от ее числителя и знаменателя отнять одно и то же число? (Дробь уменьшится.)
-
Разделите 181 пополам так, чтобы получилась 1. (
181= 101\101 = 1) -
Назовите дробь, большую 7\15, но меньшую 8\15. (1\2)
-
На одной тарелке 3\5 вкусной колбаски, на другой – 18\30 такой же вкусной колбаски. Какую тарелку ты возьмешь? (3\5 = 18\30, поэтому все равно или обе)
7. Математическая авария (резервный конкурс)
-
Устраните «неисправность» примеров:
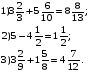 Ответы:
Ответы: 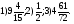
За каждое верное исправление прибавляется 1 балл, за неверное – 1 балл снимается.
-
А вот как Магистр Рассеянных Наук сокращал дроби:
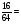
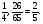

Оригинально, не правда ли? Проверьте. (Случайное совпадение.)
Этот вопрос задается устно всем. Отвечает та команда, где больше поднятых рук. За верный ответ – 2 балла.
Подведение итогов соревнования. Оценки команде и самым активным игрокам.
Рефлексия:
-
Понравилась вам игра? Какой конкурс был самым сложным для вас? Почему?
-
Какие правила пригодились вам сегодня в «сражении» с дробями?
Домашнее задание (творческое): придумать или найти занимательные задачи на дроби (2-3 задачи), решить их.
Заключение
Есть о математике молва, И за то, что в творческом труде
Что она в порядок ум приводит, Выручаешь в трудные моменты,
Потому хорошие слова, Мы сегодня искренне тебе
Часто говорят о ней в народе. Посылаем ГРОМ АПЛОДИСМЕНТОВ!
Лист жюри
| Команды | ||||
| I | II | III | IV | |
| Название команды | 1 | 1 | 1 | 1 |
| 1. Дробная перестрелка | | | | |
| 2. Раздел хлебов | | | | |
| После 2 конкурсов | | | | |
| 3. Превращение дробей | | | | |
| После 3 конкурсов | | | | |
| 4. Задача Пифагора | | | | |
| После 4 конкурсов | | | | |
| 5. Сражение с пиратами | | | | |
| После 5 конкурсов | | | | |
| 6. Конкурс капитанов | | | | |
| После 6 конкурсов | | | | |
| 7. Математическая авария | | | | |
| Дополнительные баллы | | | | |
| | | | | |
| ИТОГО | | | | |
| | | | | |
| МЕСТО | | | | |
Здесь представлен конспект к уроку на тему «СЛОЖЕНИЕ И ВЫЧИТАНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (5 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

