Презентация "Статистические методы исследования." по математике – проект, доклад
Презентацию на тему "Статистические методы исследования." можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 46 слайд(ов).
Слайды презентации
Список похожих презентаций
Математические методы исследования явлений культуры
Рекомендуемая литература: Миронов Б.Н., Степанов З.В. Историк и математика: (Математические методы в историческом исследовании). – Л., 1975. Богомолова ...статистические методы обработки данных
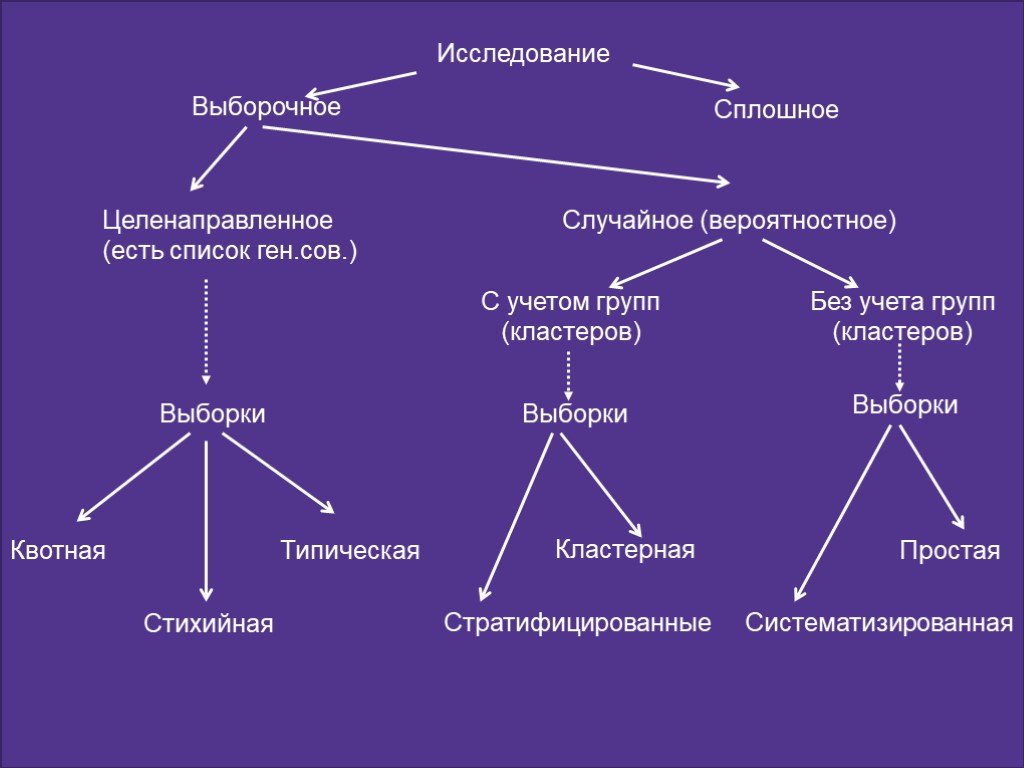
Этапы статистического исследования. 1. Сбор информации 2. Обработка информации 3. Анализ данных. Виды статистических признаков:. количественные; качественные ...Статистические исследования 5 класса МОУ «Арылахская общеобразовательная школа
Цель: выяснить, как собираются и группируются статистические данные, как можно наглядно представить статистические исследования . уточнение понятия ...Формы и методы подготовки к ЕГЭ на уроках математики
«…подготовка к ЕГЭ стала сегодня основной целью работы учителя. А результаты ЕГЭ – основным мерилом его работы». Нарышкин С. Е., глава специальной ...Статистические характеристики интервального ряда
Тема урока: «Статистические характеристики интервального ряда». Тип урока: повторительно - обобщительный урок. Цели и задачи : - повторить основные ...Статистические характеристики
“Статистика знает всё”. “Известно, сколько какой пищи съедает в год средний гражданин республики… Известно, сколько в стране охотников, балерин, станков, ...Статистические характеристики
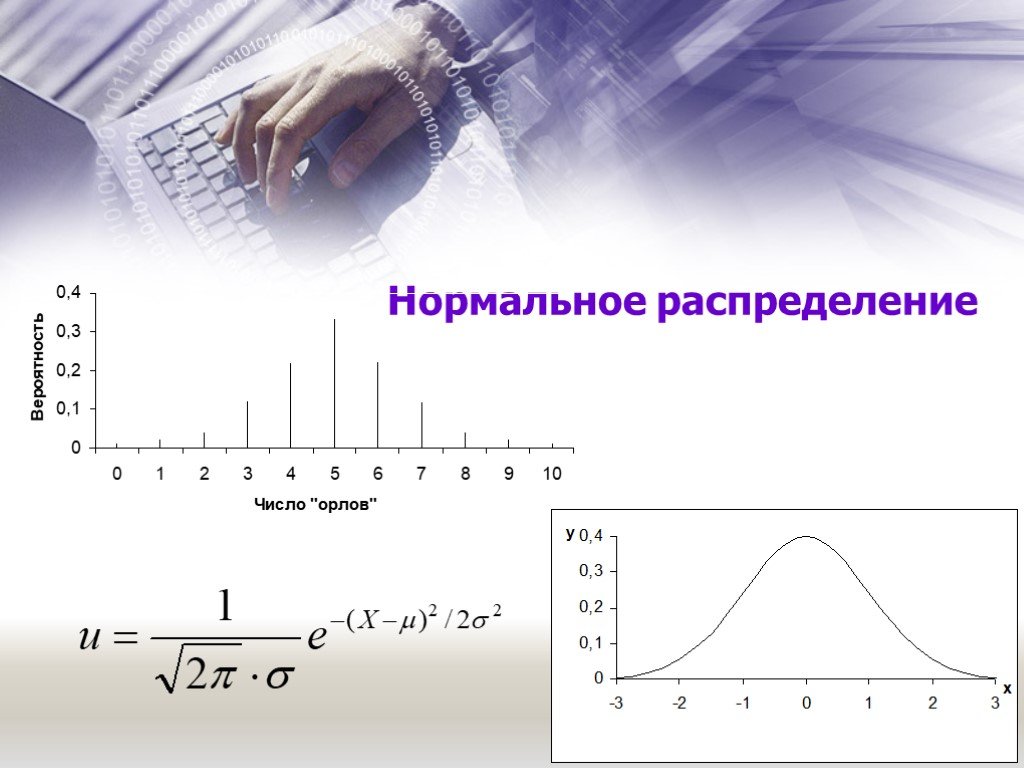
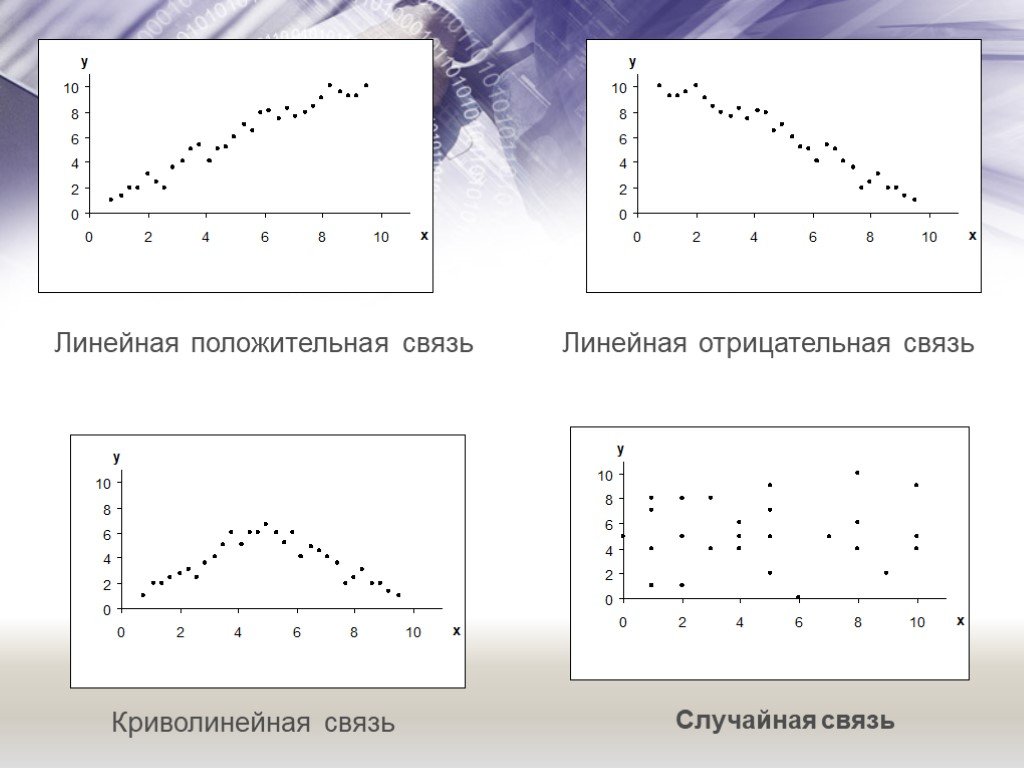
Среднее арифметическое, размах и мода находят применение в статистике – науке, которая занимается получением, обработкой и анализом количественных ...Статистические распределения и их основные характеристики
Различия индивидуальных значений признака у единиц совокупности называются вариацией признака. Она возникает в результате того, что индивидуальные ...Системы линейных уравнений: методы решения
Систему m линейных уравнений с n неизвестными будем записывать в следующем виде:. Здесь x1, x2, , xn – неизвестные величины; aij (i = 1,2, … , m; ...Активные методы обучения на уроках математики и во внеурочной деятельности
Активные методы обучения — это методы, которые побуждают учащихся к активной мыслительной и практической деятельности в процессе овладения учебным ...Применение производной для исследования функций
Монотонность функции. Убывает на (-;x, x) Возрастает на х1; х2. Постоянна на а;в. у х У=f(x) x1 а в. Исследование функции на возрастание. ...Комбинаторные методы решения вероятностных задач
Обобщить знания и умения учащихся по применению методов решения задач формировать умения решать задачи на нахождение вероятности случайного события ...Математические методы в сетевом планировании
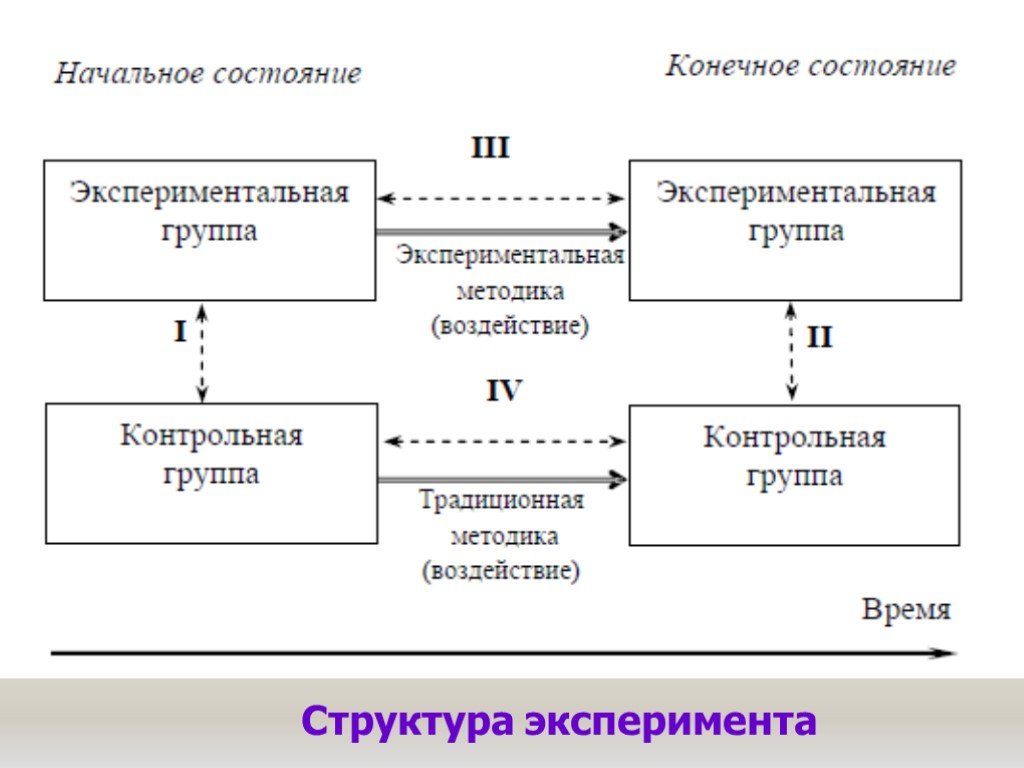
Сергей Гриняев Угрозы информационной революции Угрозы и вызовы - среднесрочный прогноз экспертов корпорации РЭНД о будущем информационной революции. ...Исследование операций и методы оптимизации
Структура дисциплины. Лекции – 32 ч. Практические занятия – 32 ч. ОТЧЕТНОСТЬ Контрольная работа - 5 ТЕСТЫ - 1 ФОРУМ - 1 Экзамен. ВВЕДЕНИЕ В ИССЛЕДОВАНИЕ ...Грубые погрешности и методы их устранения
Определение. Грубая погрешность, или промах, — это погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий ...Аналитический и численный методы решения систем уравнений с параметром
АНАЛИТИЧЕСКИЙ И ЧИСЛЕННЫЙ МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ С ПАРАМЕТРОМ. Астрахарчик Н.А. Система симметрична относительно знака x. Система симметрична ...Аналитические методы решения логарифмических уравнений
Цели урока:. Обобщить и систематизировать изученные методы решения логарифмических уравнений Выявить особенности каждого метода Выяснить, всегда ли ...Активные формы и методы обучения школьников
Ф о р м ы р а б о т ы. индивидуальные парные групповые коллективные. Основные формы проведения факультативных занятий. Лекция Семинар Дискуссия Решение ...Применение производной для исследования функции на монотонность и экстремумы
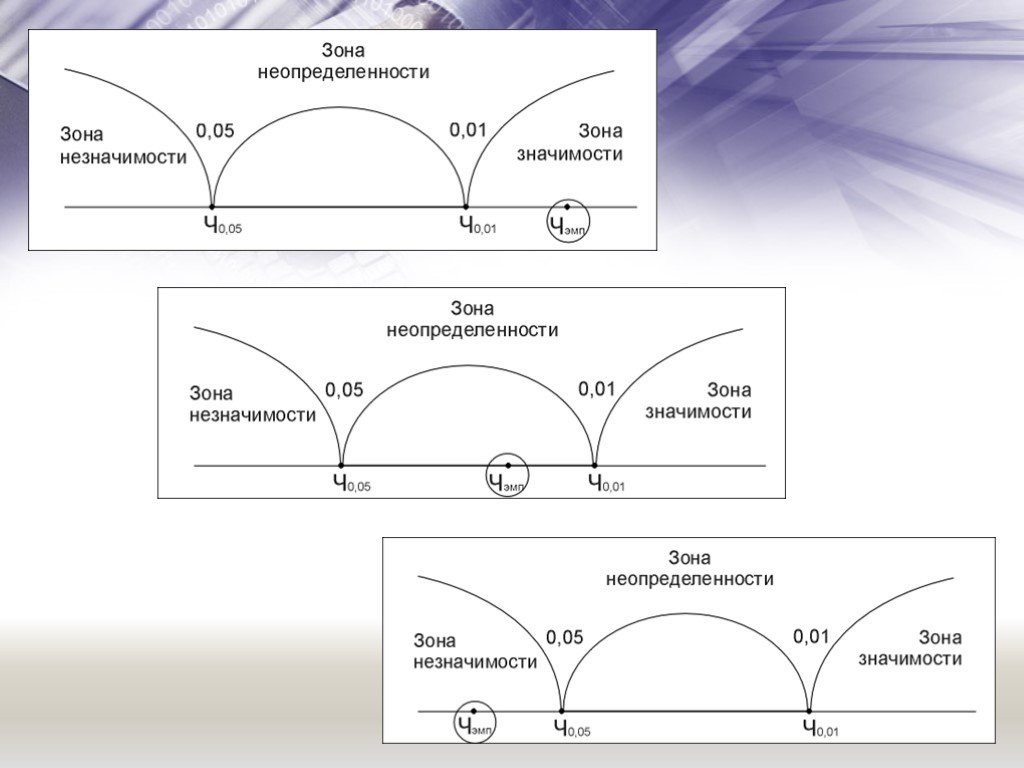
Х У 0 касательная α. k – угловой коэффициент прямой (касательной). Геометрический смысл производной: если к графику функции y = f(x) в точке с абсциссой ...Математические методы проверки гипотез
Гипотеза – это…. Гипотеза исследования. Теоретическая: объясняет причины и внутренние закономерностей эмпирически исследуемых явлений. Эмпирическая: ...Конспекты
Численные методы интегрирования
Государственное бюджетное образовательное учреждение. среднего профессионального образования. Пермский политехнический колледж имени Н.Г. Славянова. ...Статистические характеристики
Нелюбина Гульнара Ахуновна. Моау «СОШ №10» город Оренбург. Учитель математики. Разработка урока по теме «Статистические характеристики». 7 класс. ...Статистическое определение вероятности. Комбинаторные методы решения задач
Алгебра. Раздел: Теория вероятностей. Тема:. Статистическое определение вероятности. Комбинаторные методы решения задач. Цель:. выработать умение ...Статистика. Статистические характеристики
Учитель: Ахонен Екатерина Петровна. Урок в 8 классе по теме: « Статистика. Статистические характеристики». Цель:. . Познакомить с понятиями ...Статистические характеристики
. Технологическая карта урока математики. . 1. Ф.И.О. учителя:. Орликова Наталья Ивановна. . 2. Класс: 7. Дата: 07.10.2013 . . . Предмет:. ...Применение производной для исследования функций на монотонность и экстремумы
Открытый урок по математике в 10 классе по теме:. «Применение производной для исследования функций на монотонность и экстремумы». Цели и задачи:. ...Применение производной для исследования функций на монотонность и экстремумы
Урок алгебры в 10 классе. по теме: «Применение производной для исследования функций. . на монотонность и экстремумы». Тип урока:. . интегрированный. ...Общие методы решения уравнений
Разработка урока в 11 классе. . Тема урока: Общие методы решения уравнений. Цели:. Повторить и расширить сведения об уравнениях и способах ...Основные методы решения тригонометрических уравнений
. МАТЕМАТИКА 11 класс. Тема: Основные методы решения тригонометрических уравнений. Цели урока:. Обобщить и систематизировать полученные знания ...Общие методы решения тригонометрических уравнений
. Муниципальное общеобразовательное учреждение. Малоибряйкинская основная общеобразовательная школа. Похвистневского района Самарской области. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:25 сентября 2018
Категория:Математика
Содержит:46 слайд(ов)
Поделись с друзьями:
Скачать презентацию