Презентация "Элементы комбинаторики" по математике – проект, доклад
Презентацию на тему "Элементы комбинаторики" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 61 слайд(ов).
Слайды презентации
Список похожих презентаций
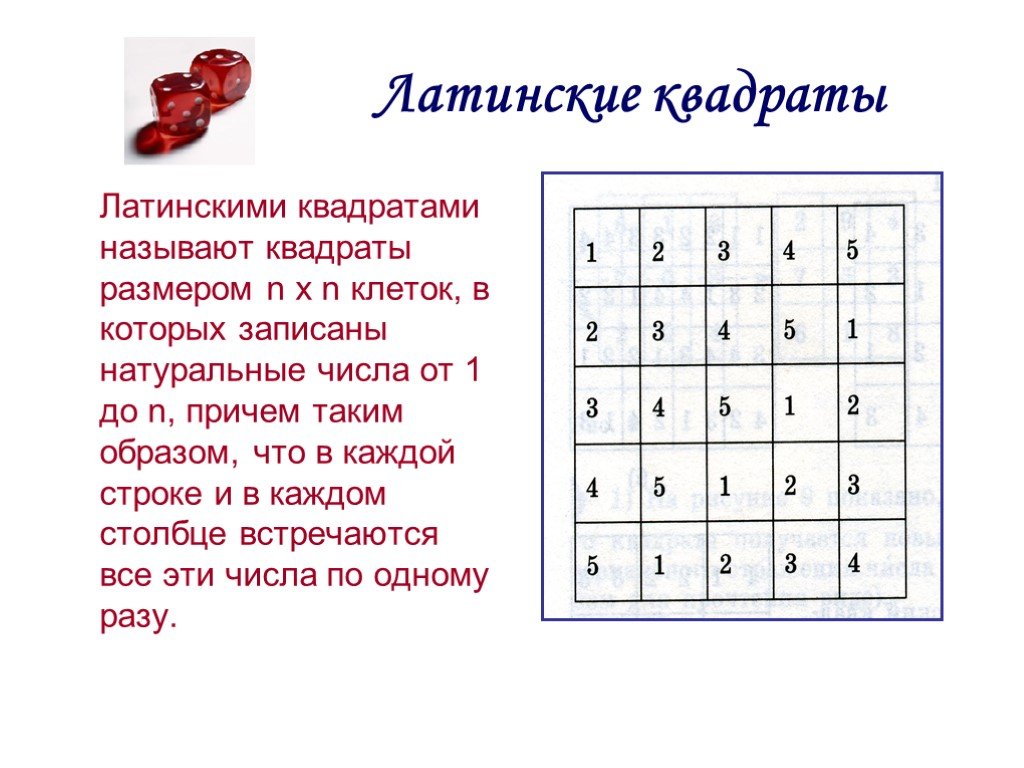
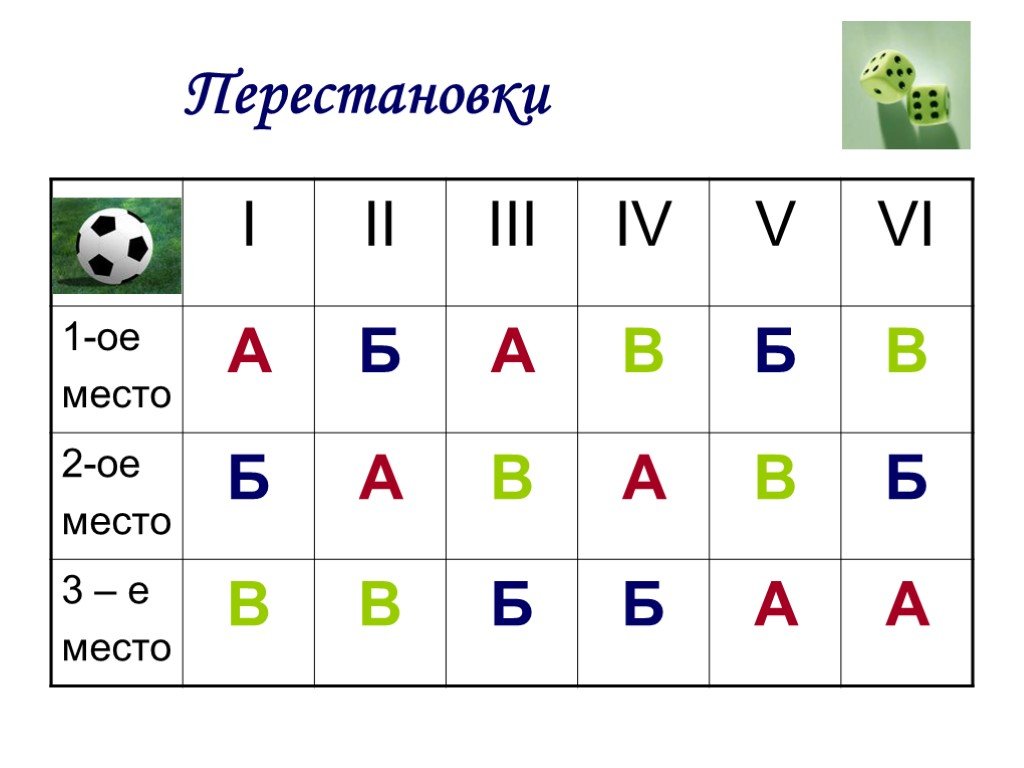
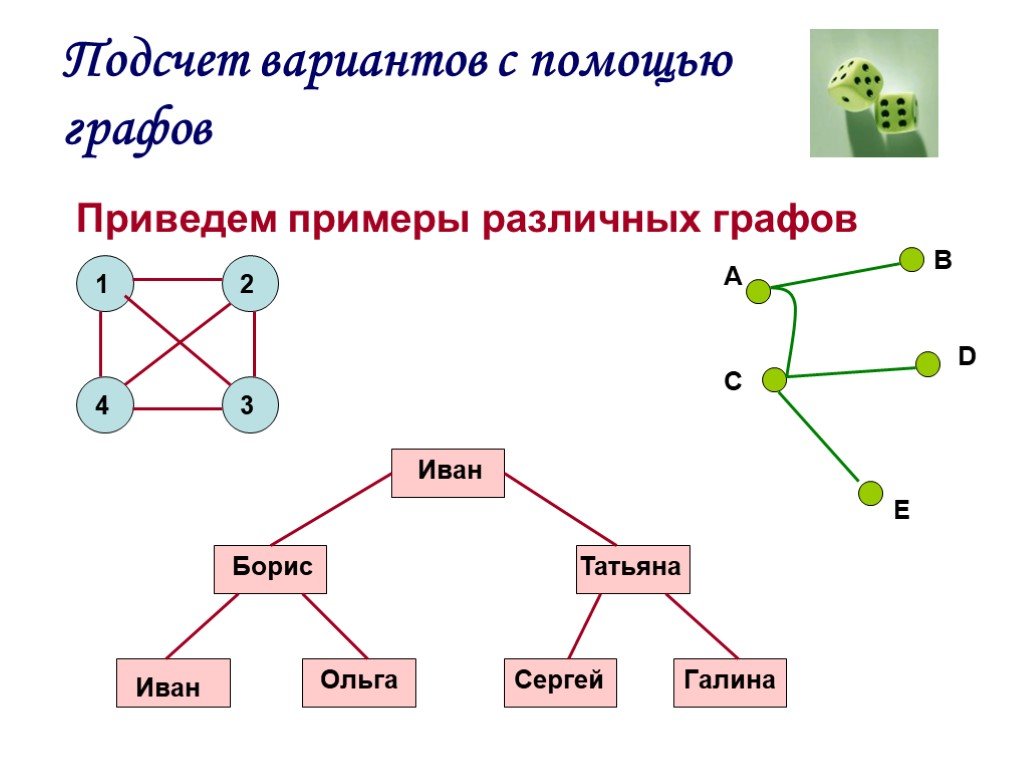
Элементы комбинаторики
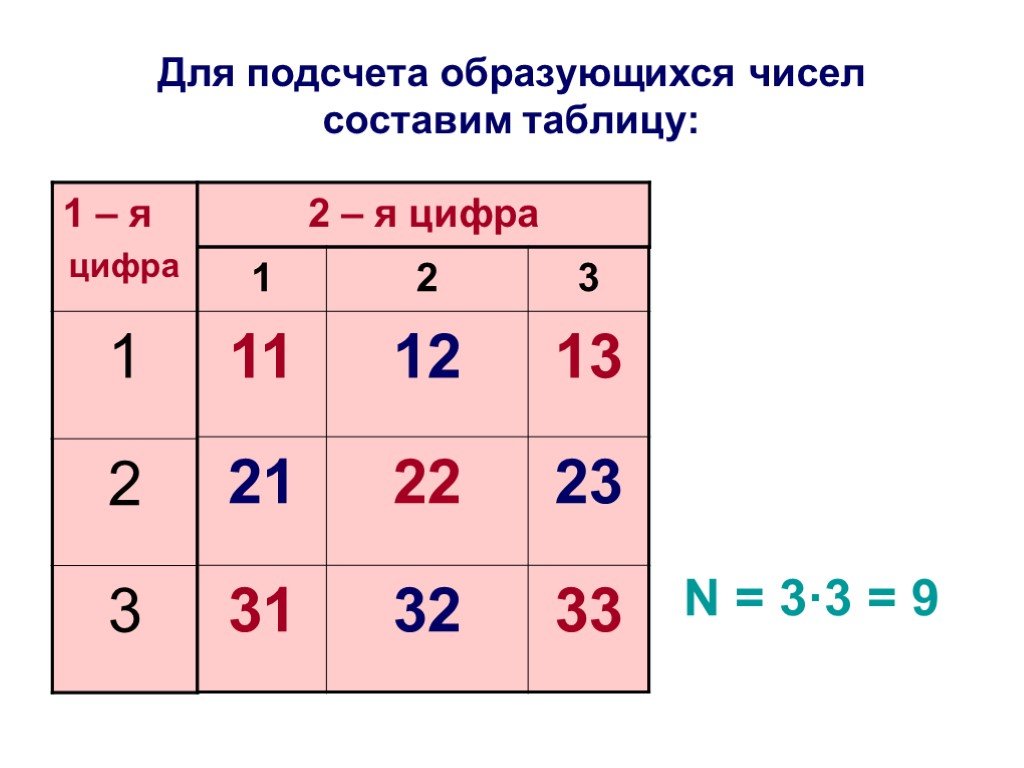
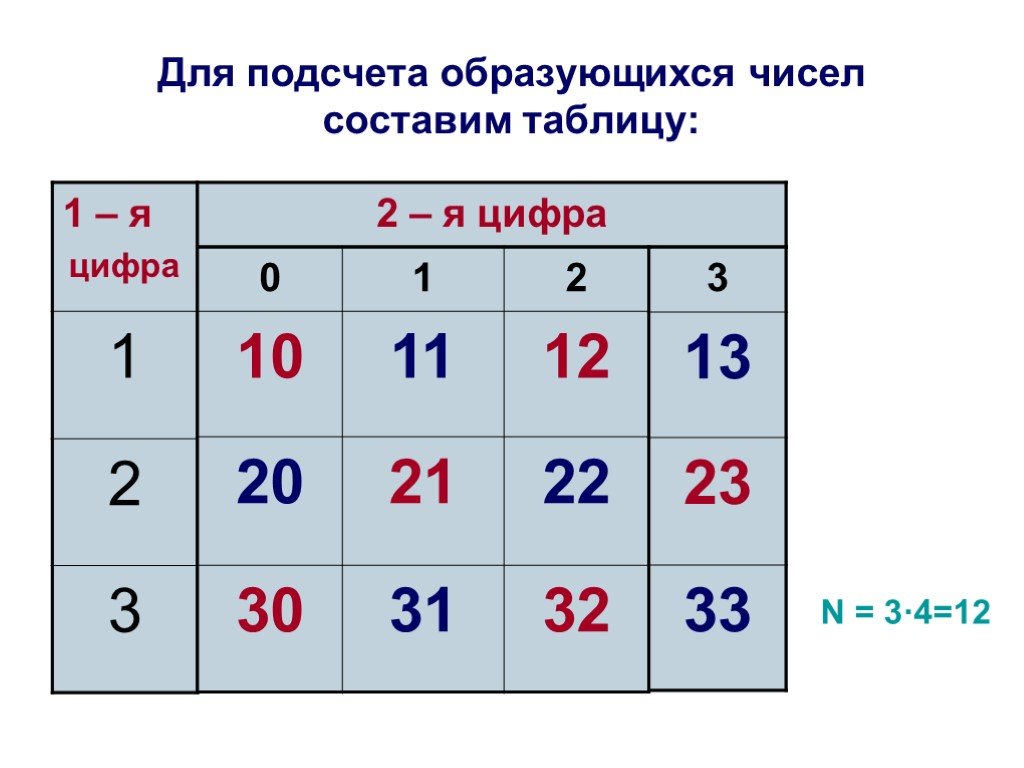
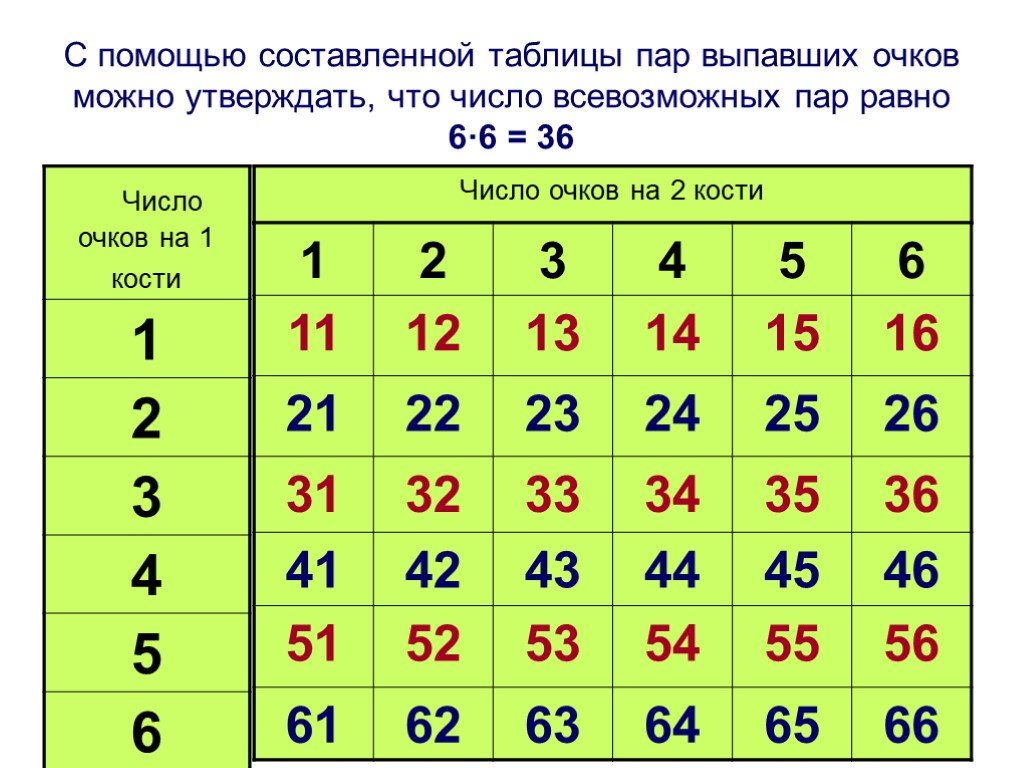
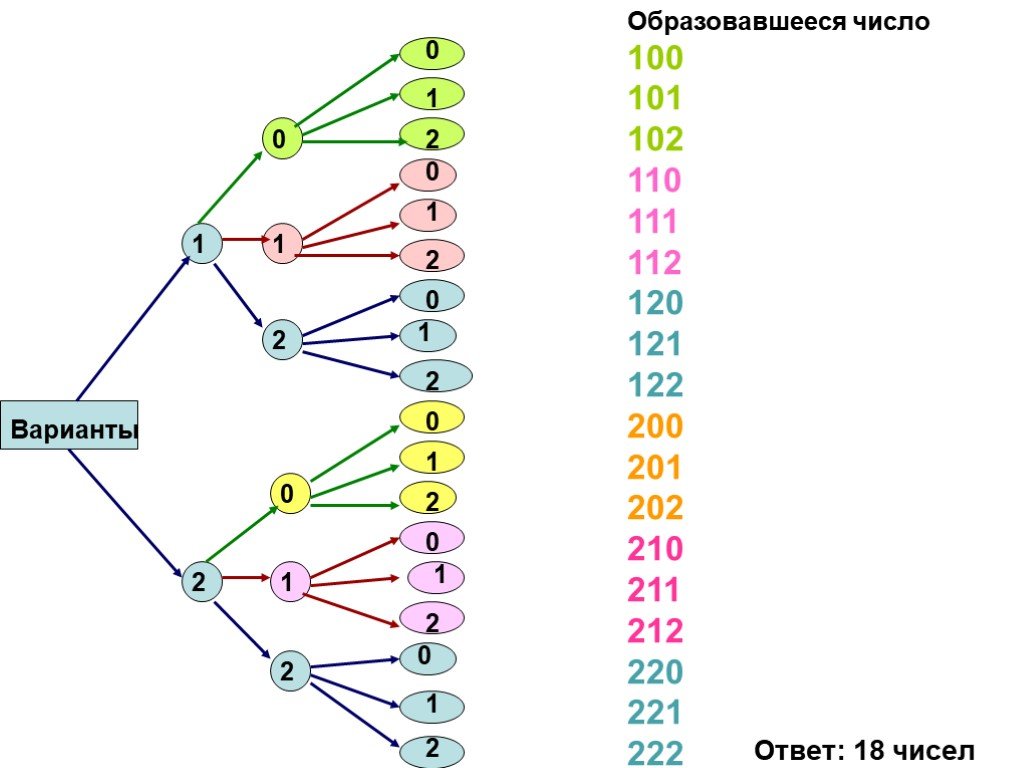
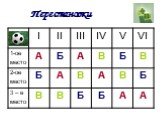
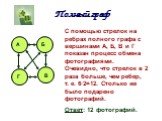
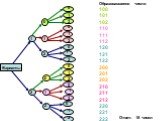
Принцип произведения комбинаций. N = n1 ∙ n2 ∙ … ∙ nk. Пусть имеется k групп элементов, причем i-я группа содержит ni элементов, 1 ≤ i ≤ k. Выберем ...Элементы математической статистики, комбинаторики и теории вероятностей. Сочетания и размещения. Часть I
Содержание. Введение Пример 1. Учительница подготовила к контрольной работе… Решения: 1.а) 1.б) 1.в) 1.г) Пример 2. Известно, что х = 2аЗb5с и а, ...Элементы математической статистики
Содержание. Введение Генеральная совокупность и выборка Способы отбора Статистическое распределение выборки Эмпирическая функция распределения Статистические ...Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильного многогранника
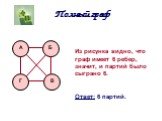
Цель урока: Ознакомление с понятием симметрии в пространстве и с понятием правильного многогранника. Задачи урока: Ввести понятие правильного многогранника, ...Элементы теории графов
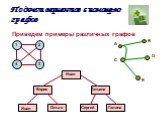
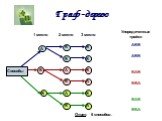
Цели реферата:. Изучить существующие теории графов. Научиться применять эти теории при решении логических задач. Расширить объем нетрадиционных приемов ...Методика изучения элементов комбинаторики в условиях профильного обучения математике
Содержание. Введение Глава 1. Цели изучения стохастической линии в школе 1) Из истории комбинаторики 2) Цели изучения стохастики в школе Глава 2. ...Элементы статистики
Цель проекта:. Обобщить знания по теме «Элементы статистики»,решать задачи по теме. («Алгебра» 7,8 класс, под редакцией С.А.Теляковского). Определение ...Элементы теории вероятностей
Содержание:. Предмет теории вероятностей n! Перестановки Размещения Сочетания События Вероятность события Условная вероятность Сумма вероятностей ...Элементы правильных многогранников
Содержание:. Цель пректа Термин Многогранники История Платон Платоновы тела Евклид Архимед Архимедовы тела Иоганн Кеплер Космологическая гипотеза ...Элементы статистики
Статистические исследования. Сбор и группировка статистических данных. 6, 5, 4, 0, 4, 5, 7, 9, 1, 6, 8, 7, 9, 5, 8, 6, 7, 2, 5, 7, 6, 3, 4, 4, 5, ...Понятие комбинаторики
. Цели и задачи. Знакомство с новым разделом математики Рассмотреть все тонкости этого раздела Научиться решать задачи по комбинаторике. Комбинаторика ...Элементы математической статиститки
Статистика – дизайн информации. Цель:. Дать понятие генеральной и выборочной совокупности, полигону и гистограмме частот Научиться строить полигон ...Основы комбинаторики
Правило произведения Пусть объект а1 можно выбрать n1, различными способами, после каждого выбора объекта а1 объект а2 можно выбрать n2 различными ...Основные принципы комбинаторики
Комбинаторика. Комбинаторика – раздел математики, посвященный подсчету количеств разных комбинаций элементов некоторого, обычно конечного, множества ...Основные понятия комбинаторики
Содержание. Введение Понятия Правила Задачи Факториал Задачи. Введение. Комбинаторика очень важна в нашей жизни, потому что она имеет широкий спектр ...Общие понятия о симметрии. Элементы симметрии
План. Введение Термин симметрии Элементы симметрии. Введение. При обработке металла под давлением мы имеем дело с поликристаллами. Одним из важных ...Некоторые теоретико-числовые приложения комбинаторики
Примеры. Числа 2, 3, 5, 7, 11 простые, числа 4, 6, 18, 100 составные. Отметим, что число 1 не является ни простым, ни составным. Существует стандартная ...Элементы пирамиды
Цель работы:. 1).Рассмотреть историю создания пирамид 2).Основные элементы пирамид 3).Решить некоторые задачи по теме «Пирамиды» 4).Понять почему ...Элементы алгебры
Равенства и неравенства. . . Уравнения. . . . . . Неравенства. . . . . . . Буквенные выражения. ...Элементы статистики
Слово « статистика» происходит от латинского status ( состояние, положение вещей). 1. Статистика – это научное направление (комплекс наук), объединяющее ...Конспекты
Элементы комбинаторики: перестановки, сочетания и размещения
Хакимзянова Нурания Идерисовна. МБОУ «Кубянская сош» Атнинского муниципального района РТ. Учитель математики и информатики. Урок по теме "Элементы ...Элементы комбинаторики, статистики и теории вероятности
Урок-соревнование. по разделу. «Решение задач по теме «Элементы комбинаторики, статистики и теории вероятности». г.Новороссийск, ...Элементы устного народного творчества в изучении чисел на уроках математики
Учитель:. Ушакова Светлана Николаевна. Место работы:. МОУ средняя школа №10 с углубленным изучением отдельных предметов. Должность:. учитель начальных ...Элементы теории вероятности и математической статистики
Управление образования г.Астаны. ИПК и ПК СО. ГУ «Средняя школа № 36». Урок алгебры в 9 классе по теме: «Элементы теории вероятности ...Элементы теории вероятности в ГИА
13 апреля 2011г. Урок алгебры в 9 классе по теме:. . «Элементы теории вероятности в ГИА». Цели:. - Научиться анализировать и решать задачи ...Элементы математической статистики и теории вероятности
Тема урока:. Элементы математической статистики и теории вероятности. Основные цели и задачи урока:. Повторить основные понятия изучаемого предмета: ...Множество. Элементы множества. Подмножество
Муниципальное общеобразовательное учреждение. Перхушковская основная общеобразовательная школa. Конспект урока по информатике ...Многоугольники. Элементы многоугольника. Периметр многоугольника
Разработка урока по математике. 2 класс. Тема: «Многоугольники. Элементы многоугольника. Периметр многоугольника.». Цель:. формирование умения ...Многогранник. Элементы многогранника - грани, вершины, ребра
Технологическая карта урока. Математика, 4 класс «Б», учитель Сидорова О.А. Тема:. Многогранник. Элементы многогранника - грани, вершины, ребра. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 марта 2019
Категория:Математика
Содержит:61 слайд(ов)
Поделись с друзьями:
Скачать презентацию