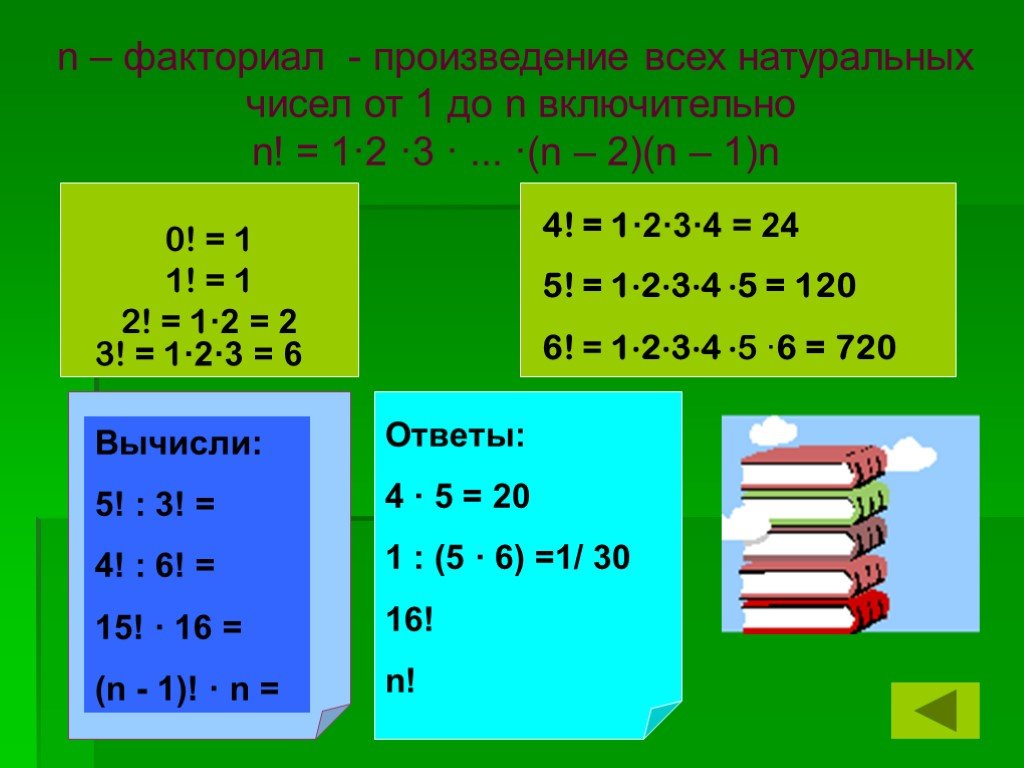
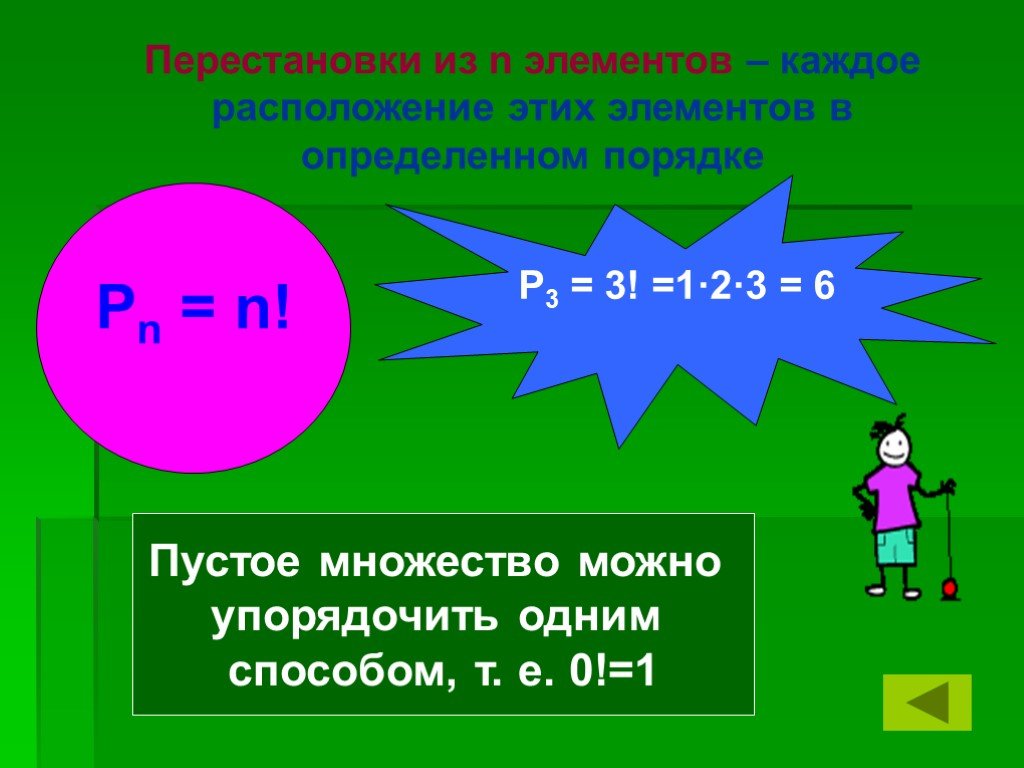
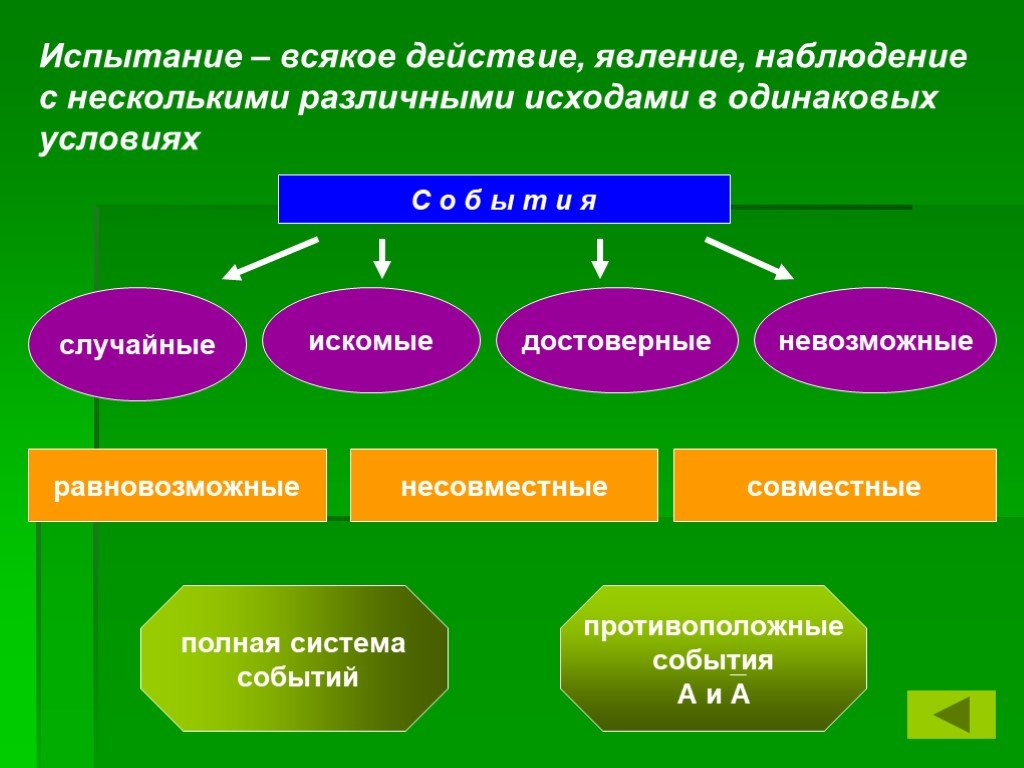
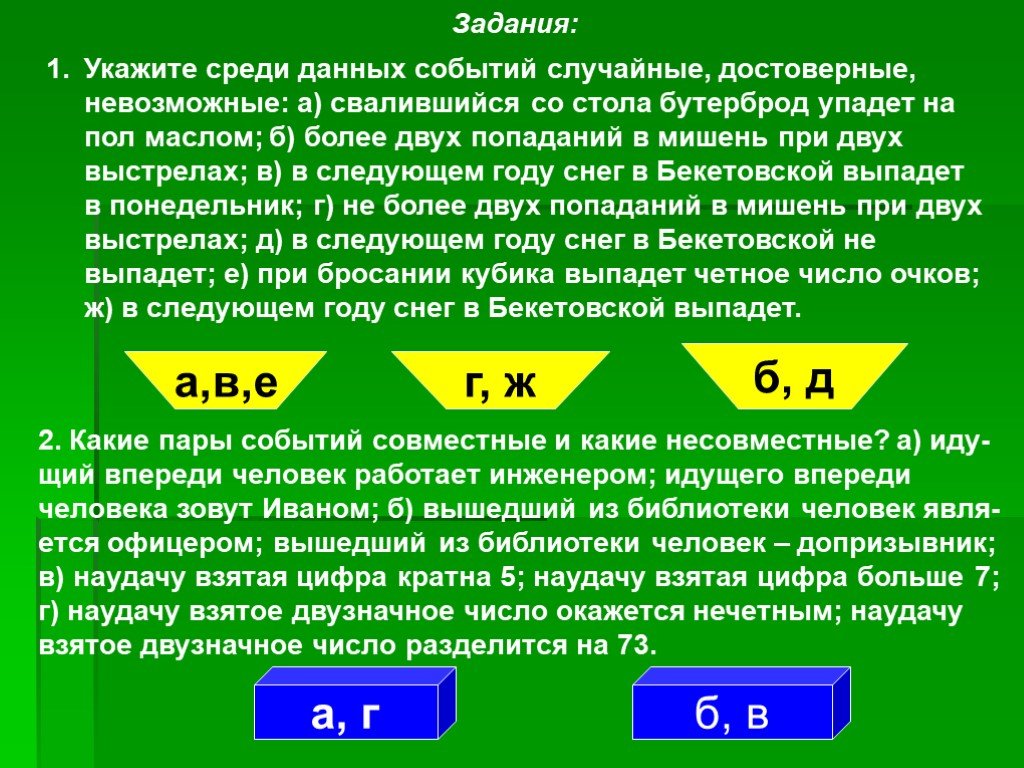
Презентация "Элементы теории вероятностей" по математике – проект, доклад
Презентацию на тему "Элементы теории вероятностей" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 22 слайд(ов).
Слайды презентации
Список похожих презентаций
Элементы теории вероятностей на ЕГЭ
Теория вероятностей. ? ЕГЭ. Теория вероятностей – раздел математики, изучающий закономерности случайный явлений: случайные события, случайные величины, ...Элементы математической статистики, комбинаторики и теории вероятностей. Сочетания и размещения. Часть I
Содержание. Введение Пример 1. Учительница подготовила к контрольной работе… Решения: 1.а) 1.б) 1.в) 1.г) Пример 2. Известно, что х = 2аЗb5с и а, ...Решение задач по теории вероятностей
Решение задач по теории вероятностей. В10. Справочный материал. Элементарные события (исходы) – простейшие события, которыми может окончится случайный ...Развитие теории вероятностей
Размещение Это любое упорядоченное подмножество m из элементов множества n. (Порядок важен). 2. Перестановки Если m = n, то эти размещения называются ...Решение задач по теории вероятностей
С.И.Ожегов, Н.Ю.Шведова «Вероятность – возможность исполнения, осуществимости чего-нибудь». А.Н.Колмогоров «Вероятность математическая – это числовая ...Применение графов в теории вероятностей
Вероятностно – статистическая линия становится сегодня неотъемлемой частью школьного курса математики. Не исключено, что задачи, связанные с вычислением ...Элементы теории графов
Цели реферата:. Изучить существующие теории графов. Научиться применять эти теории при решении логических задач. Расширить объем нетрадиционных приемов ...Основные теоремы теории вероятностей
Литература и интернет - ресурсы. Вентцель Е.С., Овчаров Л.А. Задачи и упражнения по теории вероятностей: учебное пособие. М.: Академия, 2003. – 448 ...Вводный урок "Элементы математической статистики"
Термин «статистика» произошел от латинского слова «статус» (status), что означает «состояние и положение вещей». Математическая статистика. это наука, ...Бернард Больцано и его теории
Бернард Больца́но (чеш. Bernard Placidus Johann Nepomuk Bolzano; 5 октября 1781, Прага - 18 декабря 1848) — чешский математик, философ и теолог, автор ...Элементы математической логики
Луна – спутник Земли. 2) Информатика –это наука об информации и информационных процессах. 3) Монитор – это устройство ввода информации. 4) Процессор ...Элементы комбинаторики
Принцип произведения комбинаций. N = n1 ∙ n2 ∙ … ∙ nk. Пусть имеется k групп элементов, причем i-я группа содержит ni элементов, 1 ≤ i ≤ k. Выберем ...Элементы дифференциального исчисления
Дифференциальное исчисление функций одной переменной. 1. Производные 2. Таблица производных 3. Дифференциал 4. Производные и дифференциалы высших ...Вклад философов-математиков в развитие теории многогранников
Математика: лабиринты открытий. Стереометрия как наука известна уже очень давно. Изысканиями в этой области занимались многие видные умы древности. ...Классическая формула подсчета вероятностей
Пример: выпадение герба и решки образуют полную группу событий. Группа событий называется полной, если при проведении опыта всегда происходит одно ...Алгоритмы теории игр
План лекции. Введение Матричные игры Игры с седловой точкой Смешанные стратегии Применение Итоги Литература. Введение. Первая значительная книга по ...Основы теории вероятности
Основные понятия теории вероятностей. Событием называется любой исход опыта, различают следующие виды событий: - случайные - достоверные - невозможные ...Основные понятия теории вероятности
Теория вероятностей. Введение. Основные комбинаторные объекты. Элементы теории вероятности. Задачи в которых производится подсчет всех возможных комбинаций ...Общие понятия о симметрии. Элементы симметрии
План. Введение Термин симметрии Элементы симметрии. Введение. При обработке металла под давлением мы имеем дело с поликристаллами. Одним из важных ...Независимые события. Умножение вероятностей
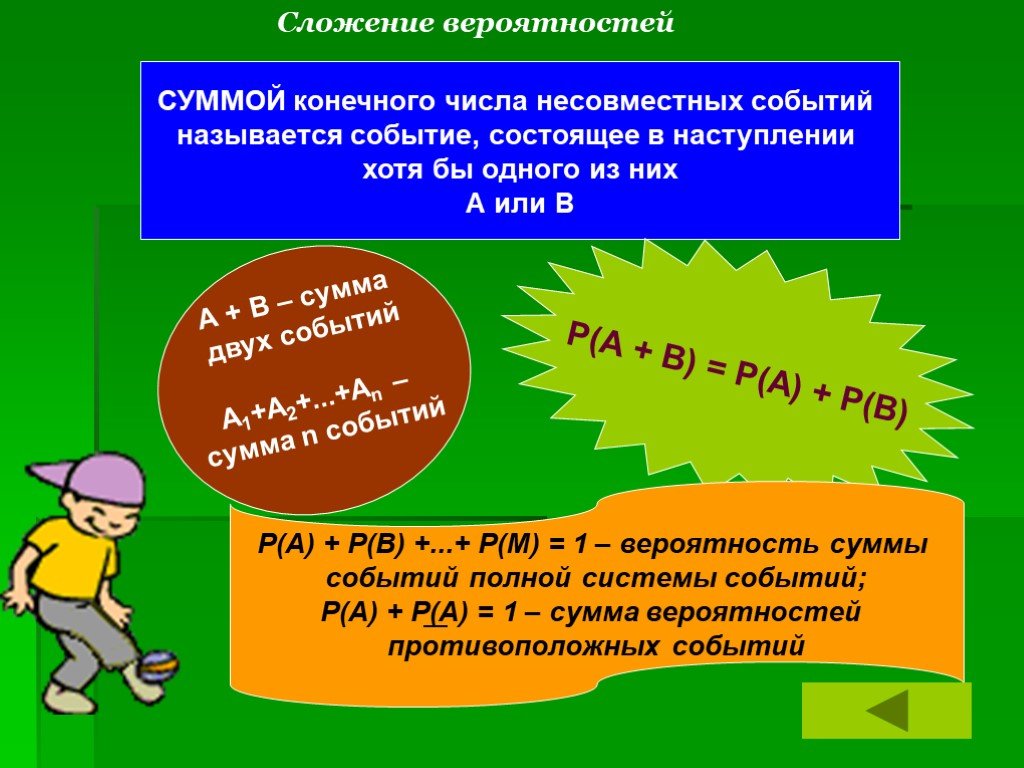
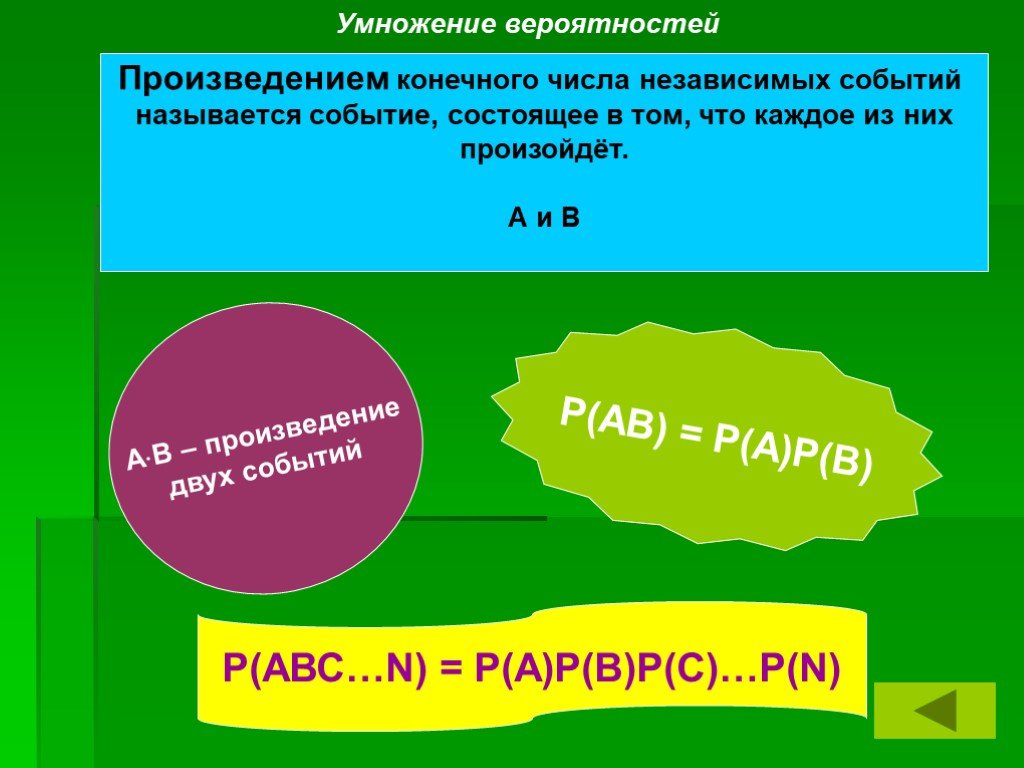
В жизни мы часто встречаемся с ситуациями, когда события некоторым образом связаны. С наступлением одного события можно судить о вероятности другого. ...Конспекты
Элементы теории вероятности и математической статистики
Управление образования г.Астаны. ИПК и ПК СО. ГУ «Средняя школа № 36». Урок алгебры в 9 классе по теме: «Элементы теории вероятности ...Элементы математической статистики и теории вероятности
Тема урока:. Элементы математической статистики и теории вероятности. Основные цели и задачи урока:. Повторить основные понятия изучаемого предмета: ...Элементы теории вероятности в ГИА
13 апреля 2011г. Урок алгебры в 9 классе по теме:. . «Элементы теории вероятности в ГИА». Цели:. - Научиться анализировать и решать задачи ...Элементы комбинаторики, статистики и теории вероятности
Урок-соревнование. по разделу. «Решение задач по теме «Элементы комбинаторики, статистики и теории вероятности». г.Новороссийск, ...Элементы устного народного творчества в изучении чисел на уроках математики
Учитель:. Ушакова Светлана Николаевна. Место работы:. МОУ средняя школа №10 с углубленным изучением отдельных предметов. Должность:. учитель начальных ...Элементы комбинаторики: перестановки, сочетания и размещения
Хакимзянова Нурания Идерисовна. МБОУ «Кубянская сош» Атнинского муниципального района РТ. Учитель математики и информатики. Урок по теме "Элементы ...Теория вероятностей
МБОУ «СОШ № 143» г. Красноярска,. . учитель математики Князькина Татьяна Викторовна. Теория вероятностей: подготовка к ЕГЭ 2014. Не так ...Теория вероятностей и комбинаторика в заданиях ЕГЭ
ШЕВЕЛЕВА НАДЕЖДА. МИХАЙЛОВНА. МОУ «Ягельная СОШ» Надымского района. Ямало-Ненецкого автономного округа. Учитель математики. ...Множество. Элементы множества. Подмножество
Муниципальное общеобразовательное учреждение. Перхушковская основная общеобразовательная школa. Конспект урока по информатике ...Многоугольники. Элементы многоугольника. Периметр многоугольника
Разработка урока по математике. 2 класс. Тема: «Многоугольники. Элементы многоугольника. Периметр многоугольника.». Цель:. формирование умения ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:19 ноября 2018
Категория:Математика
Содержит:22 слайд(ов)
Поделись с друзьями:
Скачать презентацию