Презентация "Применение интеграла к решению физических задач" по математике – проект, доклад
Презентацию на тему "Применение интеграла к решению физических задач" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 47 слайд(ов).
Слайды презентации
Список похожих презентаций
Аксиомы стереометрии Решение задач
Через любые две точки пространства проходит единственная прямая. Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная ...Алгебра высказываний. Решение логических задач
Задача 1: Составьте сложное высказывание в словесной форме из простых, заданных математическим формулировкам:. Высказывание А: «Учащийся Иванов хорошо ...Аксиомы стереометрии и их следствия. Решение задач
Цель урока: обобщение и применение аксиом и их следствий к решению задач. Математический диктант. 1). Сформулируйте аксиомы стереометрии: Аксиома ...«Решение задач по математике»
10 февраля. В классе. Задача условие вопрос решение ответ. Быстро и правильно считать. Правильно записывать решение задачи. Кричать и сердиться, когда ...«Устный счёт» математика
1- 0,4 3 +2,4 3,2 – 2 3,2- 0,2 12,3 + 3,4 2,04 + 3,6 12 – 1,5 6,2- 2,6 ( 12,4 + 3,67)- 2,67 ( 45,06 + 23,5) – 40 ,06. 0,6 5,4 1,2 3 15,7 5,64 10,5 ...«Углы» математика
Цель урока:. познакомить учащихся с геометрической фигурой углом, с видами углов (прямой, тупой, острый), сформировать представления о существенных ...«Своя игра» математика
Математическая игра-викторина «Своя игра». Конец игры Литература. Задачи – шутки 50. Вопрос: Один господин написал о себе: «Пальцев у меня двадцать ...«Своя игра» математика
Условия игры:. Участники сами выбирают темы и вопросы. Вопрос выбирает правильно ответившая команда. 210 – 250 баллов – отметка «5». 110 -200 баллов ...«Координатная плоскость» математика
Цели и задачи урока:. 1. Ввести понятие координатной плоскости, уметь определять координаты точек, строить точки по их координатам. 2. Развивать мышление, ..."Электрики и математика"
Воспитательные Воспитание умения работать в команде, уважения к сопернику, воспитание чувства ответственности; Воспитание чувства ответственности, ...Алгоритм решения простых задач
. ЗАДАЧА условие Вопрос, задание. Работа в парах. 1. Налетело 5 гусей-лебедей, подхватили и унесли братца Иванушку. 2. Печка испекла девять ржаных ...Алгоритм решения задач на пропорции
Эпиграф: «Математика обладает двумя великими сокровищами. Первое-это теорема Пифагора, второе-деление отрезка в крайнем и среднем отношении.» Иоганн ...Алггоритм. Решение задач
Задача 1. В урне хранится некоторое количество чёрных и белых шаров. Требуется разложить эти шары по двум корзинам чёрного и белого цвета: белые шары ...«Решение задач с помощью пропорций»
Найти значение Х: Х:3=4:6 5:Х=2:6 7:3=Х:18 Устная работа. Указать вид пропорциональной зависимости:. Какова зависимость пути от времени? Какова зависимость ...«Математический бой. Через тернии к звездам»
. Разминка. Сколько разных букв в названии нашей страны? 5 букв. ДВЕНАДЦАТЬ. К семи прибавить пять. Как правильно записать: одиннадцать или адиннадцать? ...Конспекты
Web -разработка. Применение производной.10 класс
ТЕХНОЛОГИЧЕСКАЯ КАРТА КОНСТРУИРОВАНИЯ УРОКА С ИСПОЛЬЗОВАНИЕ СРЕДСТВ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ. Учитель Беломестнова Наталья Петровна. Предмет, ...Алгебраические выражения. Подготовка к экзаменам
Государственное бюджетное специальное (коррекционное) образовательное учреждение для обучающихся, воспитанников с ограниченными возможностями здоровья ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:9 ноября 2018
Категория:Математика
Содержит:47 слайд(ов)
Поделись с друзьями:
Скачать презентацию














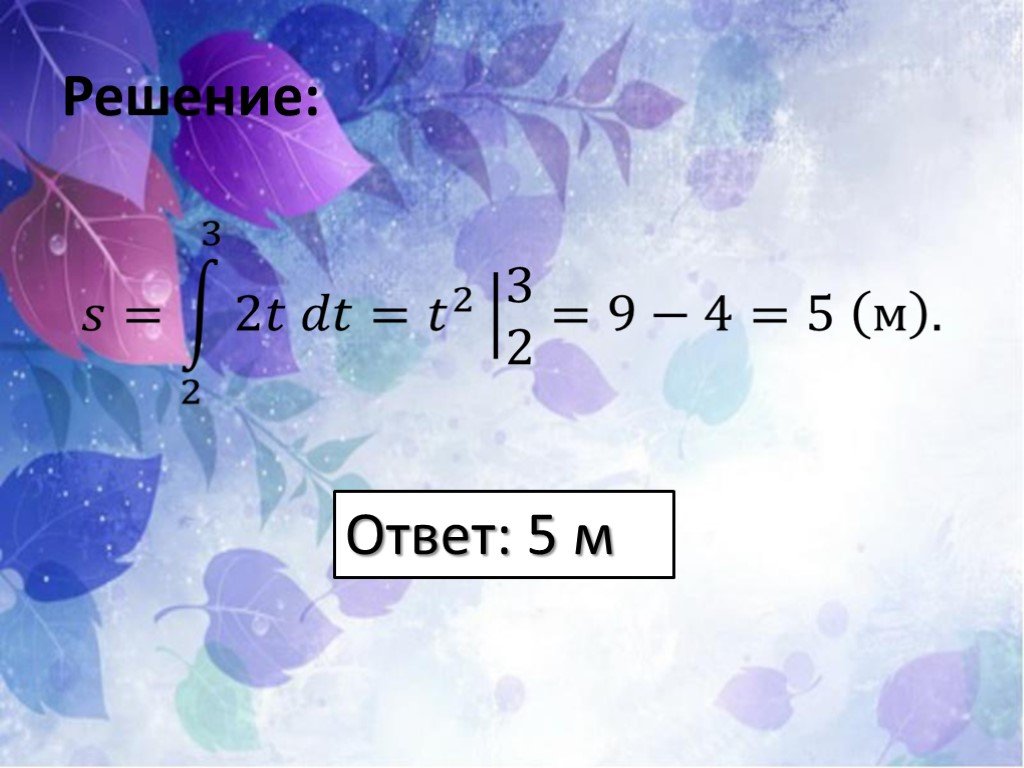









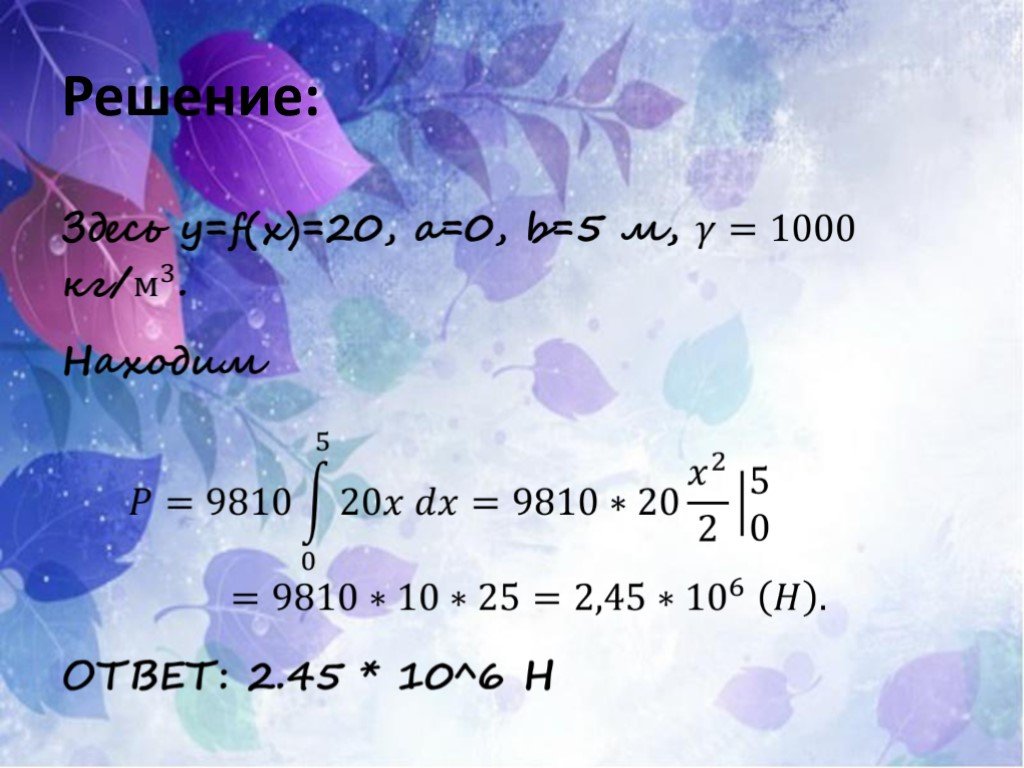






























































![№ 3 Имеется неоднородный стержень длины l. Какова масса куска стержня длины x, считая от начала, если линейная плотность ρ стержня выражается законом: 1) ρ (x) = 3x – sin 2x, x є [0; ℓ]; 2) ρ (x) = 2x + cos 3x, x є [0; ℓ]? № 4 1) Камень подброшен вертикально вверх с крыши здания высотой 20 м. Какова № 3 Имеется неоднородный стержень длины l. Какова масса куска стержня длины x, считая от начала, если линейная плотность ρ стержня выражается законом: 1) ρ (x) = 3x – sin 2x, x є [0; ℓ]; 2) ρ (x) = 2x + cos 3x, x є [0; ℓ]? № 4 1) Камень подброшен вертикально вверх с крыши здания высотой 20 м. Какова](https://prezentacii.org/upload/cloud/18/11/97647/images/thumbs/screen45.jpg)