Презентация "Пи 2" по математике – проект, доклад
Презентацию на тему "Пи 2" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 31 слайд(ов).
Слайды презентации
Список похожих презентаций
История числа Пи
Впервые обозначением этого числа греческой буквой воспользовался британский математик Уильям Джонс в 1706 году, а общепринятым оно стало после работ ...Интересные факты о числе Пи
«Лицо π было скрыто маской. Все понимали, что сорвать её, не сможет никто…» Бертран Рассел. Хронология вычисления числа ПИ. Практические способы вычисления ...Загадочное число Пи
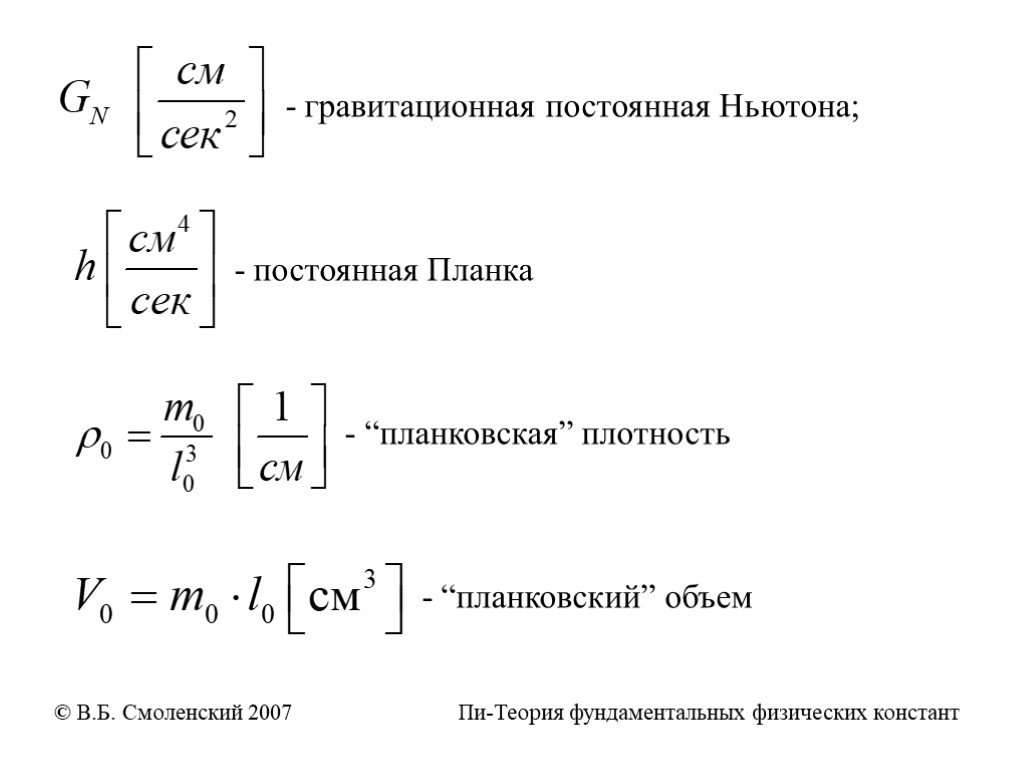
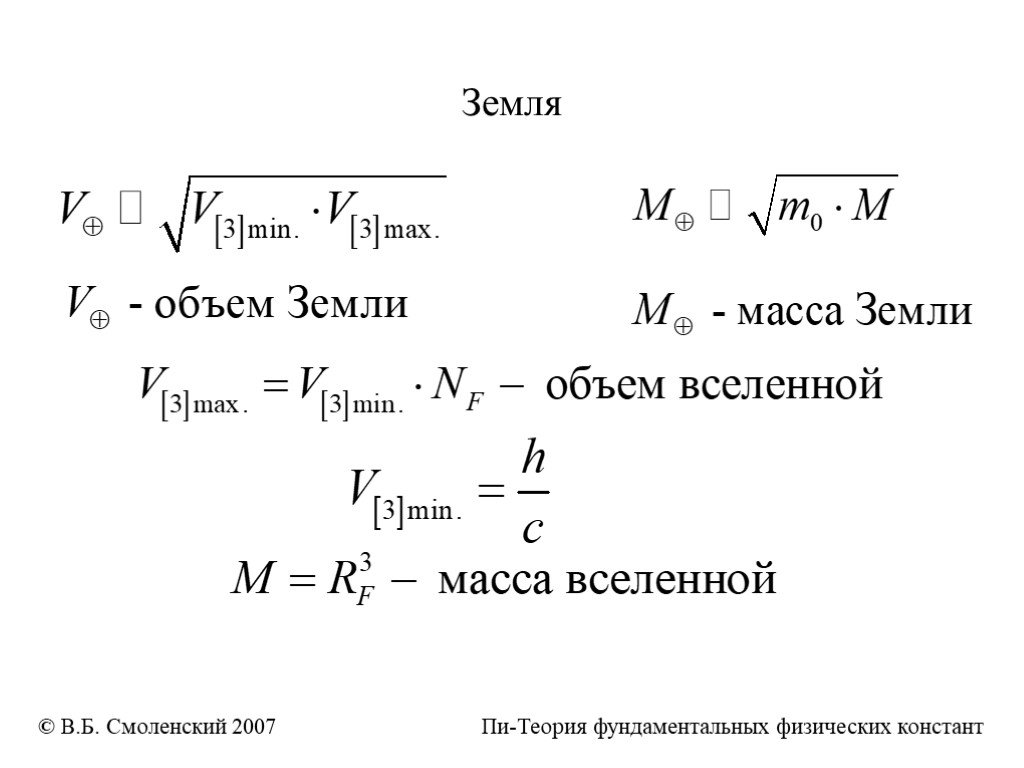
Пи, несомненно, одна из наиболее универсальных и фундаментальных констант, известных Человечеству. В силу своей универсальности Пи используется в ...Вычисления значения числа Пи
Число π – это хаос. Периферия – окружность. Известно много формул с числом π:. Франсуа Виет: Формула Валлиса:. Выражение через полилогарифм:. И многие ...Алгебра и геометрия
Комплексные числа. ׳. Содержание. § 1. Основные понятия § 2. Геометрическое изображение комплексных чисел § 3. Формы записи комплексных чисел § 4. ...Наглядная геометрия
геометрия Урок 1. Сегодня мы отправляемся в путешествие в удивительную страну, которая называется ГЕОМЕТРИЯ. Что такое геометрия? Какими инструментами ...Наглядная геометрия для начальной школы
Содержание. Урок 1 Урок 2 Урок 3 Урок 4. Урок 1 Путешествие в страну Геометрия. Знакомство с веселой Точкой. Начнем урок. Наша школьная страна. Не ...Лобачевский и его геометрия
Гипотеза:. Любая теория современной науки считается единственно верной, пока не создана следующая. Невозможность доказать некоторое геометрическое ...Математика геометрия
ГЛАВА 1. История математики. ГЛАВА 2. Математика. ГЛАВА 3. Геометрия И последнее…. Что такое математика. Она изучает числа и величины, отношения и ...Занимательная геометрия
КРОССВОРД Т О Ч К А. П Р Я М О Й. О Т Р Е З О К. О К Р У Ж Н О С Т Ь. К В А Д Р А Т. Л У Ч. На каком из рисунков клеточки А2, В1, С3 закрашены? На ...Зачем нужна наука геометрия?
Что означает термин геометрия??? Из истории возникновения геометрии. Где изучают геометрию? Виды углов. Виды треугольников. Зачем нужна геометрия??? ...геометрия решение задачи
Дано: а-прямая, A B а Построить: BC=2AB Решение:. A,B-точки на прямой,. (на луче BA). Измерим циркулем расстояние между A и B,. отложим отрезок AC ...Живая геометрия
Цель проекта :. - создание художественно-оформительной студии Пютагорас; Коллекция открыток и коллекция ювелирных изделий. Задачи проекта :. Образовательные: ...Алгебра и геометрия
История. Женщина обучает детей геометрии. Иллюстрация из парижской рукописи Евклидовых «Начал», начало XIV века. Средние века немного дали геометрии, ...«Скалярное произведение векторов» геометрия
Таблица значений для углов, равных 300, 450, 600. Заполните таблицу. Формулы приведения. sin( )= cos( )= -. Проверка д.з. № 1039 Диагонали квадрата ...«Симметрия в пространстве» геометрия
Что такое симметрия? Симметрия в переводе с греческого означает соразмерность. Под симметрией принято понимать свойство геометрической фигуры, расположенной ...«Ломаная» геометрия
Найдите соответствие. Ответы. Ломаная Тема урока:. Какие из фигур являются ломаными? А Б В Г Д. Ответ А В Г. Кусок проволоки возьми И его ты перегни. ...«Конус» геометрия
История изучения геометрического тела конус. С именем Евклида связывают становление александрийской математики (геометрической алгебры) как науки. ...Древняя геометрия
еликие учёные древности. Развитие математики происходило в древнегреческой школе, основателем которой был легендарный Пифагор (564-473 г.г. до н. ...В моде – геометрия
Мода 60 – ых, и поп - арт. Наряды с геометрическими формами смотрятся очень остро. В моде 1920-х годов большое влияние оказало авангардное искусство-от ...Конспекты
Длина окружности. Число Пи
Муниципальное автономное общеобразовательное учреждение средняя общеобразовательная школа №36 г. Томска. Конспект урока математики в 6 классе. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:1 октября 2019
Категория:Математика
Содержит:31 слайд(ов)
Поделись с друзьями:
Скачать презентацию