Конспект урока «Длина окружности. Число Пи» по математике для 6 класса
Муниципальное автономное общеобразовательное учреждение средняя общеобразовательная школа №36 г. Томска
Конспект урока математики в 6 классе
по теме «Длина окружности. Число Пи»
Тип урока: изучение нового материала
Учитель математики: Демчук И.В.
Цели урока:
-
Повторить знания об окружности и её элементах
-
Познакомить учащихся с числом пи и историей его открытия
-
Вывести формулу для нахождения длины окружности
-
Отработать умение решать задачи с применением этой формулы
-
Повысить интерес к предмету
-
Развитие познавательной активности, творческих способностей, смекалки и сообразительности
-
Прививать навык самостоятельности в работе, учить трудолюбию и аккуратности
Структура урока:
-
Организационный момент
-
Формулировка темы и цели урока
-
Выполнение практической работы
-
Историческая справка о числе пи
-
Изучение нового материала
-
Закрепление изученного материала при решении задач
-
Тест на проверку усвоения знаний и умений
-
Запись и комментирование домашнего задания
-
Подведение итогов урока
-
Рефлексия
Оборудование: проектор, презентация, ножницы, нитки, линейки, модели кругов.
Ход урока:
-
Организационный момент
-
Объявление темы и целей урока
Вступительное слово учителя
Сегодня мне хочется начать наш урок необычно - я вам загадаю загадки, а вы попробуете их отгадать.
Нет углов у меня
И похож на блюдце я
На тарелку и на крышку,
На кольцо, на колесо,
Кто же я такой друзья? (круг)
У круга есть одна подруга,
Знакома всем её наружность.
Она идет по краю круга
И называется (окружность)
Сегодня наш урок посвящен окружности, а именно мы научимся находить длину окружности. Вы наверное, удивитесь, как такое возможно, но немного терпения.
Древние греки считали окружность совершенной фигурой, самой круглой. И в наше время в некоторых случаях. Когда хотят дать особую оценку используют слово круглый, как синоним слова «полнейший»- «круглый отличник», «круглый сирота».
Какие элементы окружности вам известны? Давайте восстановим определения соединив стрелками начало и конец определения
| |
|
|
|
|
|
|
|
|
Да, вы замечательно знаете определения, а теперь посмотрим, сможете ли вы найти хорду, диаметр и радиус на чертеже
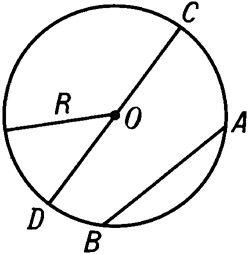
Окружность самая простая кривая линия. Слово радиус происходит от латинского и означает «спица колеса», хорда - греческого происхождения и означает «струна», диаметр в переводе « поперечник».
-
Практическая работа
У каждого из вас на руках по три модели круга с разным радиусом. Сейчас мы найдем длину опоясывающей его окружности. К сожалению, линейкой это трудно сделать, и специального инструмента у нас нет. Но это я думаю, для вас не проблема и вы предложите свои варианты решения этой задачи (учащиеся предлагают свои варианты).
Запишите результаты своих измерений в таблицу заполнив первые две колонки.
| C | D | C/D | |
| 1 | |||
| 2 | |||
| 3 |
Еще древние греки умели находить длину окружности используя одну из следующих формул С=πd или C=2πr, где С - длина окружности, d-диаметр, r-радиус. А что в этой формуле означает число π?
Π- это число, которое означает отношение длины окружности к диаметру. Открыватели числа π это люди, которые заметили, чтобы получить корзину нужного диаметра необходимо брать прутья в три раза длиннее его. Но три – это приближенное значения числа π до целых, чему же равно это значение в разряде десятых - эта проблема волновала умы человечества на протяжении многих веков.
Давайте и мы вычислим значение π и заполним последнюю колонку таблицы. Назовите свои значения π (ученики называют ответы).
Многие геометрические фигуры были известны с давних времен, в том числе и окружность. В разные временам в разных странах значения π были различны. Так, например, в Древнем Египте 3500лет назад π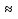 3,16; у древних римлян π
3,16; у древних римлян π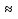 3,12. Согласно Архимеду π=22/7. Для закрепления в памяти может быть полезна шутка из учебника Магницкого:
3,12. Согласно Архимеду π=22/7. Для закрепления в памяти может быть полезна шутка из учебника Магницкого:
Двадцать две совы скучали
На больших сухих суках
Двадцать две совы мечтали
О семи больших мышах
О мышах довольно юрких
В аккуратных серых шкурках
Слюнки капали с усов
У огромных серых сов.
Еще несколько фактов из истории числа π.
-
Обозначение числа происходит от греческого perijerio «переферия», что в переводе означает окружность. Впервые обозначение использовал английский математик Уильямс Джонс в 1706 году
-
Число π в разные времена и в разных странах выражалось различным числом:
-
Греция: Архимед доказал что π одинаковое для любого круга и высчитал значение π=22/7.
-
Египет
-
Китай
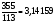
-
Индия
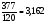
-
Россия: со времен Петра 1 наши предки занимались геометрическими расчетами в астрономии, машиностроении, корабельном деле, π
 3,1415926. Для запоминания π придумано двустишие в учебнике Магницкого, оно написано по правилам старой русской орфографии с мягким и твердым знаком «Кто и шутя и скоро пожелатъ пи узнать число ужъ знаетъ»
3,1415926. Для запоминания π придумано двустишие в учебнике Магницкого, оно написано по правилам старой русской орфографии с мягким и твердым знаком «Кто и шутя и скоро пожелатъ пи узнать число ужъ знаетъ»
-
На протяжении многих тысячелетий и вплоть до наших дней велась своеобразная погоня за десятичными знаками этого числа.
| 3знака | |
| Франсуа Виетт | 9знаков |
| Лудольф ванн Келён | 32знака |
| Рихтер | 330знаков |
| Дазе | 440знаков |
| Шенкс Уильям | 513знаков |
С появлением компьютеров погоня за знаками продолжилась
| 2037 | |
| 1961 | 100000 |
| 1973 | 10000000 |
| 1989 | 1011196691 |
| 1994 | 4044000000 |
| 1999 | 206158430000 |
-
У числа π есть свое день рождения, он отмечается 14 марта, которое записывается в американском формате дат (месяц/день) как 3.14 и начинается в 1.59. Еще одной датой связанной с числом π является 22июля, так как в европейском формате дат записывается как 22/7. В этот день в Италии едят ПИццу, в Германии свиной шПИк, в Англии жареную ПИкшу, во Франции что-нибудь ПИкантное, в России стряпают ПИроги.
-
Решение задач. Практическое применение полученных знаний.
Заполните таблицу, найдя длину окружности по известному радиусу или диаметру, найдите радиус и диаметр окружности по известной длине окружности.
| 5см | | 1,4м | | | |
| D | | 100дм | | | |
| C | | | | 6,28дм | 82см |
-
Первичная проверка знаний - тест: ответьте на вопросы теста, подчеркнув верный ответ
-
1.Отрезок, соединяющий две точки окружности и проходящий через центр.
А) радиус; Б) сторона; В) хорда; Г) диаметр.
-
2. Число π равно
А) 3,14; Б) 1,34; В) 3,91; Г) 4,13.
-
3. Формула длины окружности
А) С=πr Б) С=πd В) C=2πd Г) C=2r
-
4. Чему равен диаметр окружности, радиус которой 3,8 см?
А) 6,28 Б) 1,57 В) 7,6 Г) 3,14
-
5. Найдите длину окружности радиус которой 1,5дм
-
А) 6,28 Б) 3 В) 9,24 Г) 4,71
-
Запись и комментирование домашнего задания
В соревнованиях по фигурному катанию на велосипедах спортсмену необходимо проехать 5 кругов по окружности радиусом 3м. Какое расстояние проехали спортсмены?
-
Подведение итогов урока. Рефлексия.
Оцените свою работу на уроке, подчеркнув нужное продолжение предложения.
-
На уроке я работал активно/пассивно
-
Своей работой на уроке я доволен/ не доволен
-
Урок для меня показался коротким/ длинным
-
За урок я устал/не устал
-
Мое настроение за урок стало лучше/ стало хуже
-
Материал урока мне был понятен/ не понятен
-
Материал урока мне был полезен/бесполезен
-
Материал урока мне показался легким/трудным
-
Домашнее задание мне кажется интересным/не интересным
В заключение еще несколько мнемонических правил для запоминания знаков числа π.
-
Что я знаю о кругах – 3,1416
-
Это я знаю и помню прекрасно - пи многие знаки мне лишни, напрасны- 3,14159265358
-
Учи и знай в числе известном за цифрой цифру как удачу примечать- 3,14159265358
О числе π можно говорить бесконечно и вычислять его бесконечно. В настоящее время у числа уже 500 миллиардов. Это ли предел?
Спасибо Вам за урок! До новых Встреч!
Список интернет источников
Здесь представлен конспект к уроку на тему «Длина окружности. Число Пи», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (6 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

