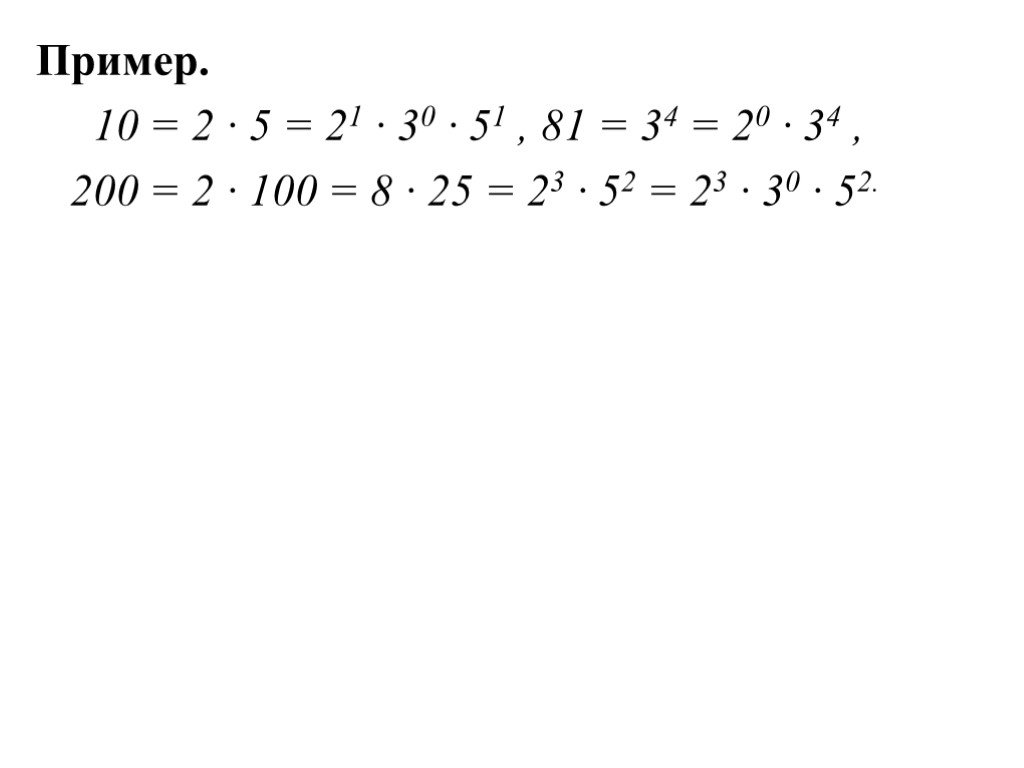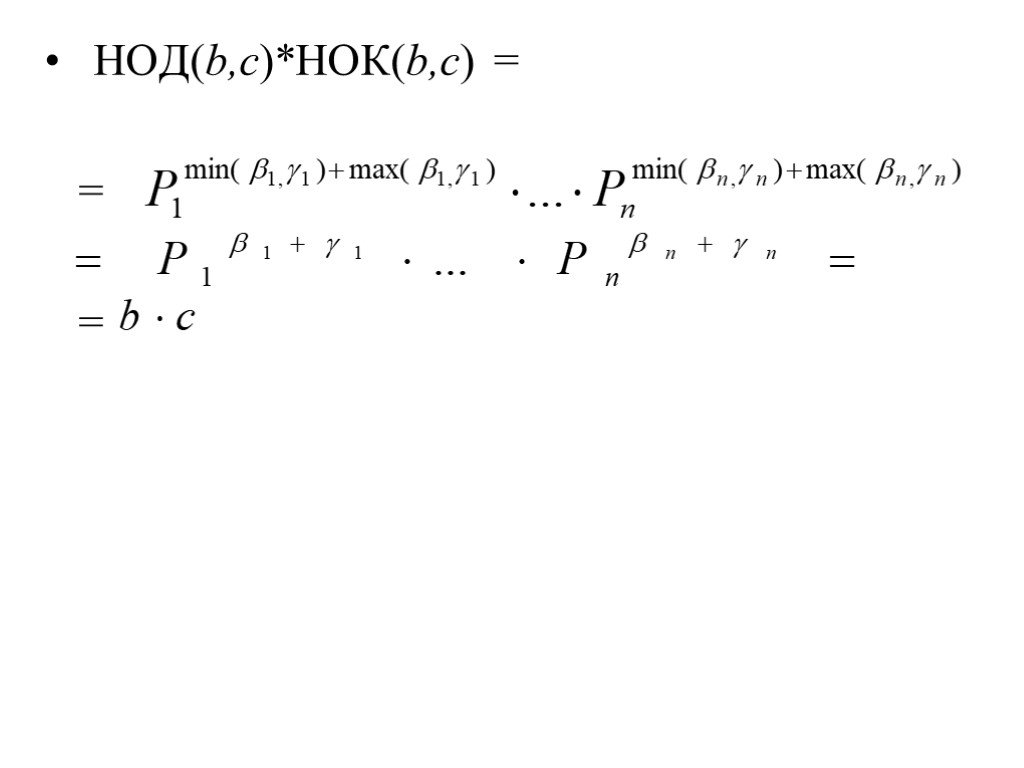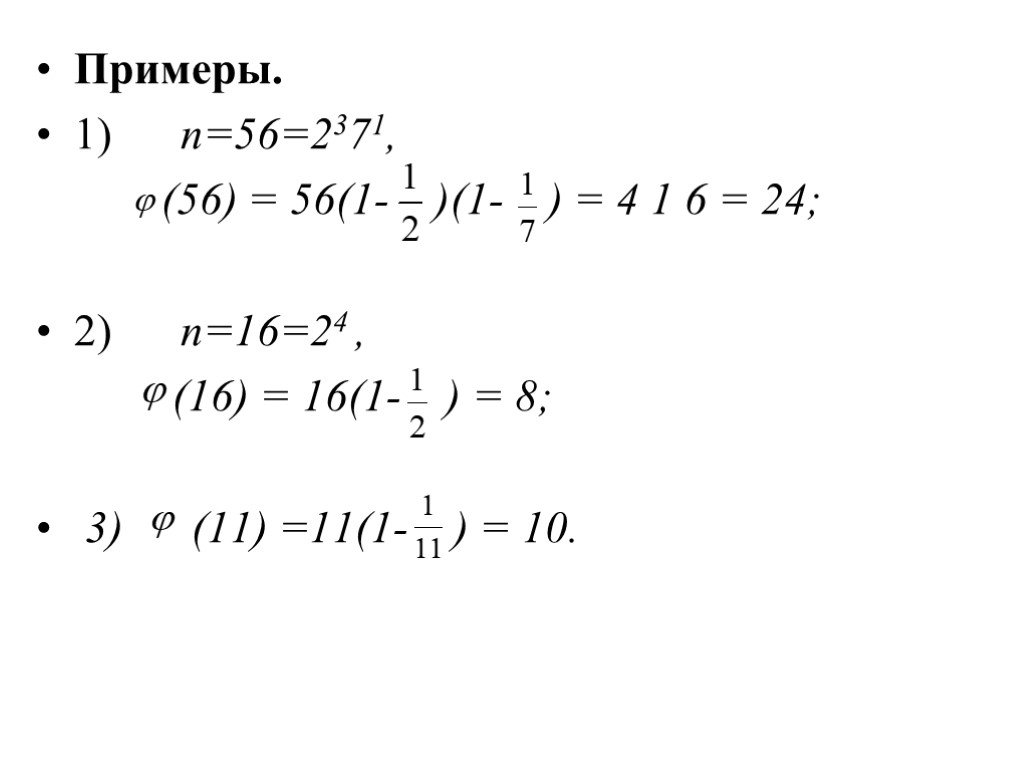Презентация "Некоторые теоретико-числовые приложения комбинаторики" по математике – проект, доклад
Презентацию на тему "Некоторые теоретико-числовые приложения комбинаторики" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 27 слайд(ов).
Слайды презентации
Список похожих презентаций
Решение тригонометрических уравнений. Некоторые способы отбора корней
№1. Расставьте знаки тригонометрических функций в зависимости от координатной четверти. Знаки синуса Знаки косинуса. Знаки тангенса и котангенса. ...Элементы комбинаторики
Введение в комбинаторику. Разработка уроков для7класса. Работа выполнена учителем математики высшей категории Вашкевич Татьяной Сергеевной. Основная ...Практические приложения подобия треугольников
Аннотация В повседневной жизни нам часто приходится сталкиваться с различными проявлениями подобия, однако подобие в обыденном смысле и с математической ...Основы комбинаторики
Правило произведения Пусть объект а1 можно выбрать n1, различными способами, после каждого выбора объекта а1 объект а2 можно выбрать n2 различными ...Понятие комбинаторики
. Цели и задачи. Знакомство с новым разделом математики Рассмотреть все тонкости этого раздела Научиться решать задачи по комбинаторике. Комбинаторика ...Основные понятия комбинаторики
Содержание. Введение Понятия Правила Задачи Факториал Задачи. Введение. Комбинаторика очень важна в нашей жизни, потому что она имеет широкий спектр ...Основные принципы комбинаторики
Комбинаторика. Комбинаторика – раздел математики, посвященный подсчету количеств разных комбинаций элементов некоторого, обычно конечного, множества ...Некоторые свойства прямоугольных треугольников
Математический диктант. 1. Вставьте пропущенное слово:. а) Прямой угол – это угол равный … б) Сумма углов в любом треугольнике равна …. 2. Укажите ...Некоторые следствия из аксиом
А В С Д Р Е К М А1 В1 С1 Д1 Q P R. 2) №1 (в,г); 2(б,д). Назовите по рисунку:. в) точки, лежащие в плоскостях АДВ и ДВС; г) прямые по которым пересекаются ...Некоторые свойства прямоугольных треугольников
ЗАДАЧИ УРОКА. РАССМОТРЕТЬ СВОЙСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ. НАУЧИТЬСЯ РЕШАТЬ ЗАДАЧИ НА ПРИМЕНЕНИЕ СВОЙСТВ ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ. СТОРОНЫ ...Некоторые применения теоремы Пифагора
Ниже будем использовать следующие обозначения: катеты и гипотенуза прямоугольного треугольника ABC соответственно a, b и c ; sin A = a / c, sin B ...Некоторые приёмы устных вычислений
Картина «Устный счёт» Николай Петрович Богданов–Бельский. ? 44 + 12 = (40 + 4) + (10 + 2) = =(40 + 10) + (4 + 2) = 50 + 6 = 56 77 + 45 = 77 + 40 + ...Элементы комбинаторики
Принцип произведения комбинаций. N = n1 ∙ n2 ∙ … ∙ nk. Пусть имеется k групп элементов, причем i-я группа содержит ni элементов, 1 ≤ i ≤ k. Выберем ...Элементы математической статистики, комбинаторики и теории вероятностей. Сочетания и размещения. Часть I
Содержание. Введение Пример 1. Учительница подготовила к контрольной работе… Решения: 1.а) 1.б) 1.в) 1.г) Пример 2. Известно, что х = 2аЗb5с и а, ...Квадратный трёхчлен и его приложения
Об авторе. Учитель математики первой категории Мальцева Надежда Геннадьевна. Пояснительная записка. Данный курс «квадратный трехчлен и его приложения» ...Методика изучения элементов комбинаторики в условиях профильного обучения математике
Содержание. Введение Глава 1. Цели изучения стохастической линии в школе 1) Из истории комбинаторики 2) Цели изучения стохастики в школе Глава 2. ...Куда пропала математика?
Замочек №1. Задача 1. Часто знает и дошкольник, Что такое треугольник. А уж вам-то как не знать! Но совсем другое дело: Очень быстро и умело Треугольники ...Интересная математика
Франция Герб Франции Флаг Франции. . Страна граничит с 8 странами: Италией, Испанией, Бельгией, Люксембургом, Германией, Швейцарией, Монако и Андоррой. ...Конкурсный урок математика
У Ромы не «3», а у Лены не «3» и не «5». Кто какую отметку получил? Проверь себя! 4 5. Запомни! . . Какую из этих схем составила Таня? I способ: 90 ...Конспекты
Элементы комбинаторики, статистики и теории вероятности
Урок-соревнование. по разделу. «Решение задач по теме «Элементы комбинаторики, статистики и теории вероятности». г.Новороссийск, ...Практические приложения производной
Муниципальное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа № 22. с углубленным изучением отдельных предметов. ...Умножение положительных и отрицательных чисел. Некоторые экологические проблемы города вокруг нашей школы
. ФИО Фадина Светлана Николаевна, Фонская Ирина Сергеевна. Место работы МБОУ СОШ № 2 г. Конаково Тверской области. . . . Должность учитель ...Площади параллелограмма и треугольника, приложения для нахождения площадей различных фигур
Дата. . Тема:. Площади параллелограмма и треугольника, приложения для нахождения площадей различных фигур. Цель:. познакомиться с формулой Пика ...Практические приложения подобия треугольников
Муниципальное образовательное учреждение. . «Морская кадетская школа им. адмирала Котова П. Г.». Урок по геометрии (8 кл.). Тема: «Практические ...Некоторые следствия из аксиом стереометрии
Государственное образовательное учреждение. . начального профессионального образования. «Профессиональное училище №5» г. Белгорода. ...Некоторые свойства прямоугольных треугольников. Решение задач
Тема урока. : «Некоторые свойства прямоугольных треугольников. Решение задач». Цель:. расширить знания учащихся о прямоугольных треугольниках. ...Некоторые свойства прямоугольных треугольников
«Некоторые свойства прямоугольных треугольников». . . Цели урока:. рассмотреть некоторые свойства прямоугольного треугольника и показать, как они ...Логарифмическая функция и ее приложения
Урок математики для физико-математического профиля. . 10- 11 класса. . . Тема: «Логарифмическая функция и ее приложения». . Цели урока:. ...Логарифмическая функция и её приложения
Тема урока. «Логарифмическая функция и её приложения». Цель урока: * расширить представление учащихся о логарифмической. функции, применении ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:9 июля 2019
Категория:Математика
Содержит:27 слайд(ов)
Поделись с друзьями:
Скачать презентацию