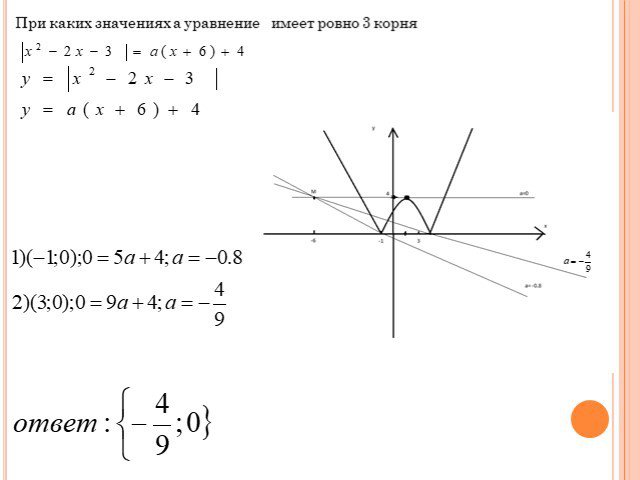
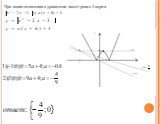
Презентация "Практикум по решению задач с параметрами" по математике – проект, доклад

Практикум по решению задач с параметрами

Введение

Решение уравнений и неравенств,содержащих параметры, является одним из самых трудных разделов элементарной математики.Для их решения обычно требуются гибкость мышления, логика в рассуждениях , умение хорошо и полно анализировать ситуацию. В последние годы задачи с параметрами регулярно встречаются в вариантах ОГЭ и ЕГЭ, но до сих пор задача с параметром остаётся самой « неудобной». Опыт показывает, что учащиеся владеющие методами решения задач с параметрами, успешно справляются и с другими задачами.

Параметр ( от греческого"отмеривающий»)-величина, значения которой служат для различения элементов некоторого множества между собой.

Если в уравнении или неравенстве наряду с неизвестной величиной входят неизвестные, но фиксированные числа, обозначаемые буквами, то они называются параметрами. Примеры параметрических уравнений и неравенств: ах=3;2х-5в=8;( 2а+3)х²-ах+1=0;ах-х²>12

Специфика уравнений (неравенств) с параметром состоит в том, что изменение значений параметра влечет за собой изменение не только коэффициентов, но и ряда других характеристик

Степень уравнения( например, уравнение ах² -3х +6=0 при a=0 является линейным, а при а≠0-квадратным) Характер монотонности функции (например, функция y= loga x при а>1 является возрастающей, а при 00: ОДЗ: x≥0, при a

В отношении уравнений(неравенств )чаще всего встречаются две постановки задачи.

для каждого значения параметра найти все решения заданного уравнения(неравенства) Найти все значения параметра, при каждом из которых решения уравнения(неравенства) удовлетворяют заданным требованиям

Линейные уравнения с параметром

Рассмотрим уравнения, которые после преобразования приводятся к линейным уравнениям вида ах=в, где а и в параметры При решении таких уравнений необходимо рассмотреть два случая: а=0 и а≠0

Примеры решения уравнений с параметром

Решите уравнение а²(х-1) +6х=(5х-2)а После преобразований данное уравнение примет вид (а-2)(а-3)х=а(а-2) Исследуем случаи, когда коэффициент при х равен нулю и когда отличен от нуля. Если а=2. То уравнение принимает вид 0х=0 Решением полученного уравнения является любое действительное число. Если а=3, уравнение примет вид 0х=3. Решений нет Если а ≠ 3; а ≠2, то х=а:(а-3) Ответ: при а=2 х -любое действительное число; приа=3 решения нет; при а ≠ 2 и а ≠3 , то х=а:(а-3)

Упражнения

= Корней нет

По О.Д.З.

а) определить количество корней уравнения в зависимости от а

0

Ответ : a1.5 , два корня

Решить уравнение

Ответ: при a при -410 ; х=-0,5а+2

При каких а уравнение имеет ровно один корень

При каких значениях a уравнение

имеет ровно 3 корня

Определить количество корней в зависимости от значений параметра m: m2x+4m+4=4x+3m2 Решение. Преобразуем уравнение: m2x-4x+3m2-4m-4, (m2-4)x=3m2-4m-4. Разложим на множители выражения, стоящие в левой и правой частях уравнения: (m-2)(m+2)x=3 (m-2). Проведя рассуждения, аналогичные рассуждениям при реше- нии примеров 1-3, получим ответ. Ответ: если m≠ ±2, то одно решение, ели m= 2, то решений бесконечно много; если m= -2, то решений нет.

Литература. 1)С.К.Кожухов. «Уравнения и неравенства с параметром .» г.Орел 2013 2)Л.Солуковцева. «Линейные и дробно-линейные уравнения и неравенства с параметрами»г.Москва 2007