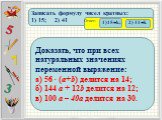
Презентация "Свойства делимости" (5 класс) по математике – проект, доклад

Свойства делимости Урок № 1

Математика 5 класс

Пестова Любовь Ивановна, УВК «Школа-гимназия» № 10, г. Симферополь

Разминка

Три плюс три умножить на три. Сколько будет? У треугольника срезали один угол. Сколько углов останется? Сколько концов у трех с половиной палок? Шла старуха в Москву, а навстречу ей три старика. Сколько человек шло в Москву? Петух весит на одной ноге 4 кг. Сколько весит петух на двух ногах? Три курицы за три дня несут три яйца. Сколько яиц снесут двенадцать кур за двенадцать дней?

Задача: Из порта А в порт В одновременно вышли два теплохода. Первый из них тратит на рейс туда и обратно 3 суток, а второй 4 суток. Через сколько суток оба теплохода окажутся снова вместе в порту А?

Решение

Числа, кратные 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, … Числа, кратные 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, … Общие кратные чисел 3 и 4: 12, 24, 36, … Наименьшее общее кратное – 12.

Определение НОК

Наименьшим общим кратным натуральных чисел а и b называют наименьшее натуральное число , которое кратно и а и b

На складе имеются гвозди в ящиках по 16 кг, 17 кг и 40 кг. Может ли кладовщик отпустить 100 кг гвоздей, не вскрывая ящика?

Решение Числа, кратные числу 16: 16;32;48;64; … Числа, кратные числу 17: 17;34;51;68; … Числа, кратные числу 40: 40;80;120;160; … Кладовщик может взять 2 ящика по 16 кг и 4 ящика по 17 кг, тогда он отпустит 100 кг гвоздей: 162 + 174 = 32 + 68 = 100 (кг). Ответ: может

Делится ли на 3 произведение: а) 6∙23∙75; б) 6∙23∙14; в) 37∙121∙19?

Свойство 1.

Если один из множителей делится на некоторое число, то и произведение делится на это число

Например, 15 делится на 3, значит, и 15  11 делится на 3, потому что 15  11= (3  5)  11 = 3  (5  11).

Решить № 595 (а,б,г)

Свойство 2.

Если первое число делится на второе, а второе делится на третье, то первое число делится на третье.

Например, 777 делится на 111, потому что 777 = 7  111, а 111 делится на 3, потому что 111 = 3  37. Из этого следует, что 777 делится на 3, так как 777 = 3  (37  7).

Решить № 596 (а, в, д)

Истинно ли утверждение: если сумма делится на 3, то и каждое слагаемое делится на 3?

Свойство 3.

Если каждое из двух чисел делится на некоторое число, то их сумма и разность делятся на это число.

Например, так как 24 : 12 и 36 : 12, то и (36+12) : 12; (36 – 12) : 12.

Решить № 603 (б, в, г)

№ 603 Решение б) (16 + 20):4 = 16:4 + 20:4= = 4 + 5 = 9; в) (50 + 120) : 5 = = 50 : 5 + 120 : 5 = = 10 + 24 = = 34; г) (484 + 426) : 2 = = 484:2 + 426:2 = = 242 + 213= = 455

Ребята, собираясь в поход, зашли в магазин, чтобы купить 6 бутылок минеральной воды и три коробка непромокаемых спичек, цену которых они не знали. Продавец назвал стоимость покупки - 213 рублей 80 копеек. Ребята попросили продавца пересчитать. Как ребята догадались, что продавец ошибся?

Рома купил в магазине 10 тетрадей, 4 ручки, несколько обложек для тетрадей по 80 коп. Продавец сказал, что нужно заплатить 27 р. 15 коп. Но Рома попросил пересчитать стоимость покупки, и ошибка была исправлена. Как он определил, что продавец ошибся в расчетах?

Свойство 4.

Если одно из двух чисел делится на некоторое число, а другое на него не делится, то их сумма и разность не делятся на это число.

Не производя вычислений, установите, делятся ли на 4 выражения: а) 132 + 360 + 536; б) 540 – 332; в) 2512·127.

Выберите число, которое можно записать в виде 4 k, где k –натуральное число.

30 15 12 18 Ответ:

Число 35 представили в виде 5  k, где k – натуральное число. Найдите это значение k.

6 8 5 7

Записать формулу чисел кратных: 1) 15; 2) 41

1)15k; 2) 41k

Доказать, что при всех натуральных значениях переменной выражение: а) 56 ∙ (а+b) делится на 14; б) 144 а + 12b делится на 12; в) 100 а – 40а делится на 30.

Домашнее задание: п. 3.1 ; решить № 596 (б, г, е), № 597, 598 (б, г, е, з)

Укажите, какие из следующих утверждений ложные. а) Если слагаемые не делятся на какое - то число, то и сумма не делится на это число. а) Ложное. Пример: 7+3 = 10; 7 и 3 не делятся на 5, а 10 делится на 5.

б) Если произведение двух чисел делится на какое - либо число, то хотя бы один из множителей делится на это число.

б) Ложное. Пример: 6 × 10 = 60; 60 делится на 15, а ни 6, ни 10 не делятся.

в) Если множители не делятся на какое - нибудь число, то и произведение не делится на это число.

в) Ложное. Пример: 6 × 10 = 60; ни 6, ни 10 не делятся на 15, а 60 делится на 15.

г) Если разность делится на какое - нибудь число, то и уменьшаемое, и вычитаемое делится на это число.

г) Ложное. Пример: 23 - 21 = 2. Разность 2 делится на 2, а 23 и 21 на 2 не делятся.

Сегодня на уроке я узнал, что… Сегодня на уроке я научился…

Спасибо за урок!