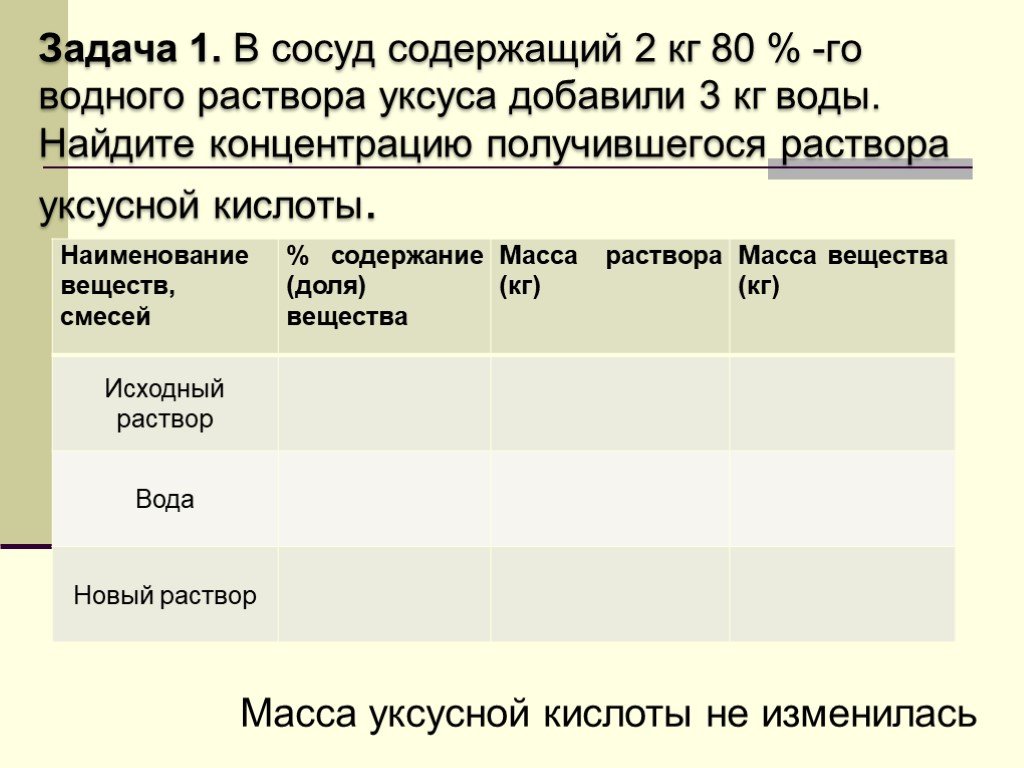
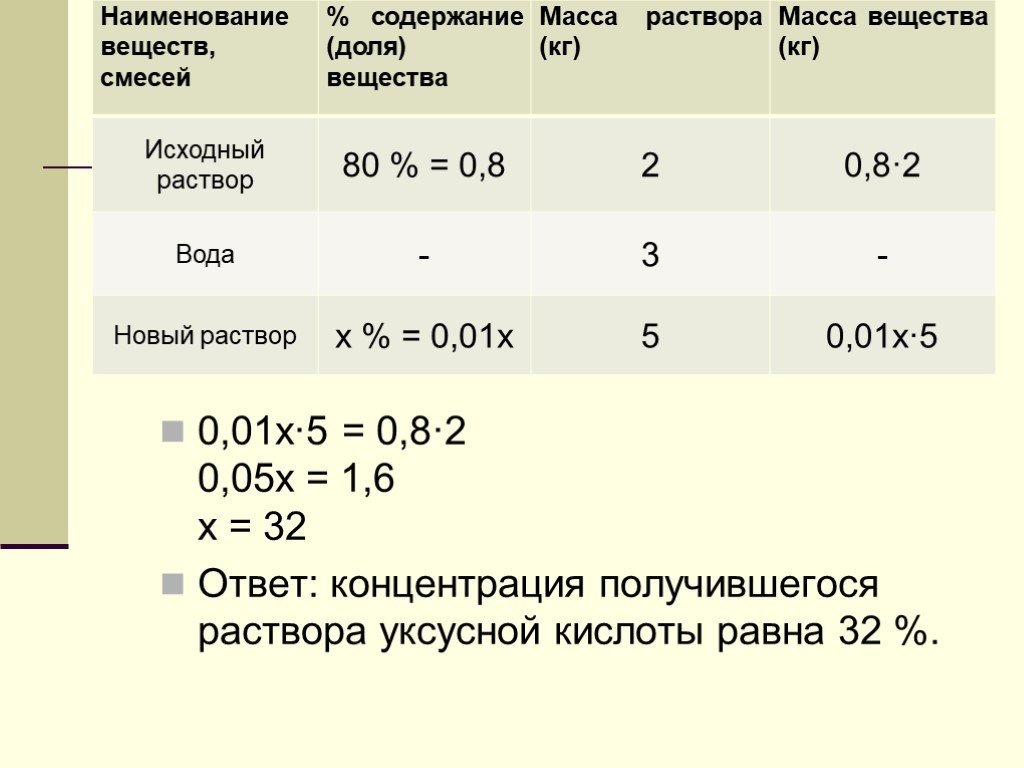
Презентация "Три основные задачи на проценты" по математике – проект, доклад
Презентацию на тему "Три основные задачи на проценты" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 14 слайд(ов).
Слайды презентации
Список похожих презентаций
«Задачи на проценты»
Тема урока: Проценты. Тип урока: урок обобщения и систематизации знаний. Цели урока: Образовательные: Обобщение и систематизация знаний учащихся о ...«Задания на проценты»
Пусть каждый день и каждый час Вам новое добудет. Пусть добрым будет ум у Вас, А сердце умным будет. (С. Маршак). Цели урока:. повторить содержание ...«Моя математика» - задачи на нахождение целого или части
МАТЕМАТИКА 1 3 4 5 7 6 8 9 0. Работа с числовым рядом. http://www.bajena.com/ru/kids/mathematics/sum-mathematics.php. 1. Прочитайте текст справа и ..."Разрезание геометрических фигур на части"
ЗАДАЧИ НА РАЗРЕЗАНИЯ. Теорема Бойяи-Гервина гласит: любой многоугольник можно так разрезать на части, что из этих частей удастся сложить квадрат. ...Арифметика Л.Ф. Магницкого. Задачи на сплавы и смеси
Цели моей работы. Познакомиться с биографией Леонтия Филипповича Магницкого Научиться решать задачи на сплавы, находить процентное содержание веществ ...Бумажные складные модели и их использование на уроках геометрии в 10 классе
Модель 1 – «Две пересекающиеся плоскости». Согнутый пополам лист бумаги служит моделью двух пересекающихся плоскостей. Линия сгиба – прямая их пересечения. ...Анания Ширакаци и его задачи
Дата рождения: около 610 год Место рождения: в области Ширак провинции Айрарат Дата смерти: около 685 год Научная сфера: математик, астроном, географ. ...Авторские задачи по математике и физике, составленные по повести Н.В. Гоголя «Ночь перед Рождеством
Методологическая основа: Класс арифметических задач огромен. Учащиеся старших классов обычно пытаются решать такие задачи алгебраически, так как владеют ...Алгоритмы работы на координатной плоскости
Цели:. Формировать умение работать на координатной плоскости как с положительными, так и отрицательными координатами. Развивать алгоритмическое мышление. ...Анализ контрольной работы по математике на тему "Натуральные числа и шкалы"
Натуральные числа и шкалы. 5 к л а с с № 1. Цели деятельности учителя. Главная дидактическая цель : организовать деятельность учащихся, направленную ..."Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
1. Найти наибольшее значение функции по её графику на [ -5;6] и [-7; 6]. 5 4 -5 у наиб. = 4 [-5; 6] у наиб. = 5 [-7; 6] 1. 2. Найти наименьшее значение ...Алгоритмы внутренних точек с приближенным решением вспомогательной задачи
1939 – линейное программирование (Канторович). 1947 – симплекс-метод (Данциг). 1967 – метод внутренних точек (Дикин). 1984 – полиномиальный МВТ (Кармаркар). ...Великие задачи математики. Квадратура круга
Автор: Монахов Станислав. МОУ "Средняя общеобразовательная школа № 59". Курск - 2006. Меня зовут Монахов Станислав. Я ученик 6-го класса, очень люблю ...Взаимное расположение прямых на плоскости
Цели:. Обобщить знания о прямых на плоскости из алгебры и геометрии 7 класса. Выяснить взаимное расположение прямых, заданных уравнением y=kx+b в ...Введение понятий "больше‒меньше" на числовом луче
1 0 5 меньше левее. 8 больше правее. 3 3 < 5 < 8 8 > 5 > 3. 3 + 5 =. . . ...Вводные задачи
Задачи на чередование. 1.На плоскости располо- жено 11 шестеренок,со- единенных по цепочке. Могут ли все шестеренки вращаться одновременно? Ответ:нет.Если ...Астрономия на координатной плоскости
Цели урока:. Закрепить полученные знания и навыки. Проявить творчество при изучении данного раздела. Избежать трудностей при изучении темы «Функция» ...Автоматизация труда учителя на примере решения систем алгебраических уравнений с использованием программного пакета MATHCAD
Ознакомить учителей математики с возможностями продукта MathCAD Обеспечить автоматизацию работы учителей с использованием MathCAD Рассмотреть решение ...Авария на промышленном объекте
Цели урока:. Повторить материал по темам “ Площади криволинейных трапеций”, “Решение показательных уравнений”, выявить пробелы в знаниях и постараться ...3 вида разложение многочлена на множители
1 вид вынесение общего множителя за скобки. Что значит разложить многочлен на множители? Разложить многочлен на множители — это значит представить ...Конспекты
Две основные задачи на дроби
. Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа № 8». Методическая разработка урока математики . ...Алгоритм решения задачи на нахождение целого и частей
. Тимошенкова. Ирина Викторовна. Учитель начальных классов. МБ НОУ «Гимназия № 70». Г. Новокузнецк. Алгоритм. решения задачи. ...Девять решений геометрической задачи
Муниципальное бюджетное общеобразовательное учреждение. «Верхнеуслонская средняя общеобразовательная школа». Верхнеуслонского муниципального района ...Данные и искомое. Их выделение в тексте задачи
МОУ СОШ № 36. Открытый урок математики во 2 классе по теме « Данные и искомое. Их выделение в тексте задачи». Учитель: Ефлаева Ф.Ш. . Тема: Данные ...Вычисление площадей фигур на клетчатой бумаге. Формула Пика
Урок геометрии в 8 классе по теме «Вычисление площадей фигур на клетчатой бумаге. Формула Пика.». (Методические рекомендации). Учитель. Берестова ...Вычисление площадей фигур на клетчатой бумаге
Фрагмент урока по теме:. . Вычисление площадей фигур на клетчатой бумаге. . . Цель :. . c. истематизация знаний по нахождению площадей геометрических ...Внетабличное деление двузначногочисла на однозначное
«Внетабличное деление двузначного числа на однозначное». Цели:. Образовательная. : формировать умение выполнять внетабличное деление двузначных ...Вместе весело шагать на экзамен
КОУ ВО «ТАЛОВСКАЯ ШКОЛА-ИНТЕРНАТ ДЛЯ ДЕТЕЙ-СИРОТ И ДЕТЕЙ, ОСТАВШИХСЯ БЕЗ ПОПЕЧЕНИЯ РОДИТЕЛЕЙ». 9 КЛАСС. ПРИГОТОВИЛИ : Гриценко Р.А. Носова ...Алгоритм письменного деления многозначного числа на двузначное, трёхзначное число
Открытый урок математики 4 класс. Тема: Алгоритм письменного деления многозначного числа на двузначное, трёхзначное число. Цель:. формирование ...Взаимосвязанные задачи с десятичными дробями
Тамбовское областное государственное автономное образовательное учреждение – общеобразовательная школа – интернат. . «Мичуринский лицей». ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:24 июня 2019
Категория:Математика
Содержит:14 слайд(ов)
Поделись с друзьями:
Скачать презентацию