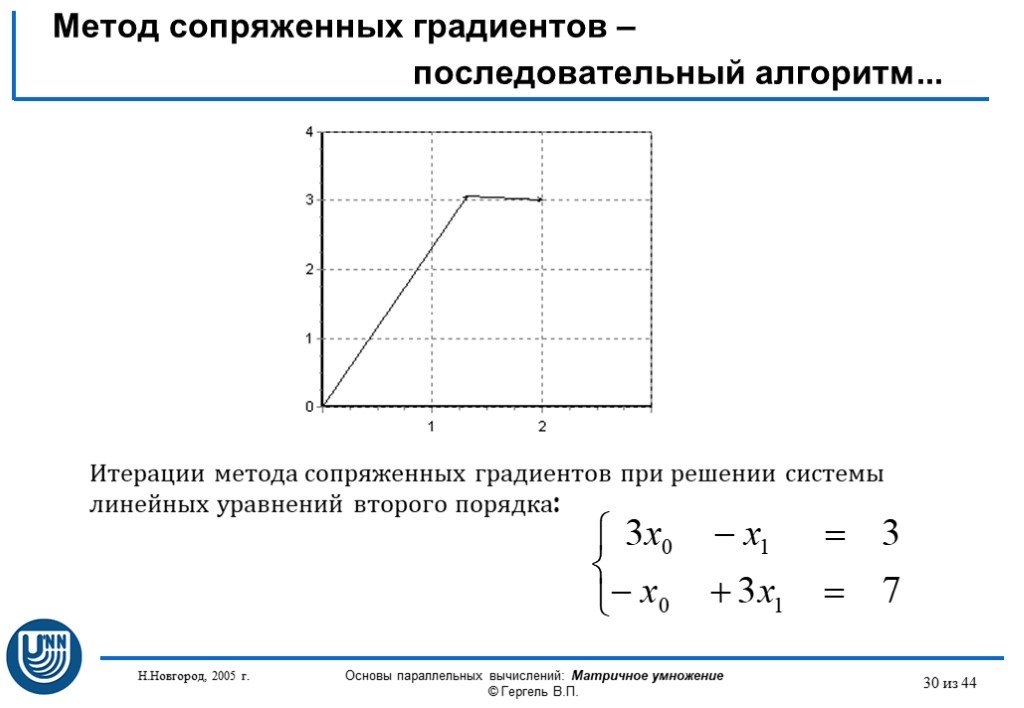
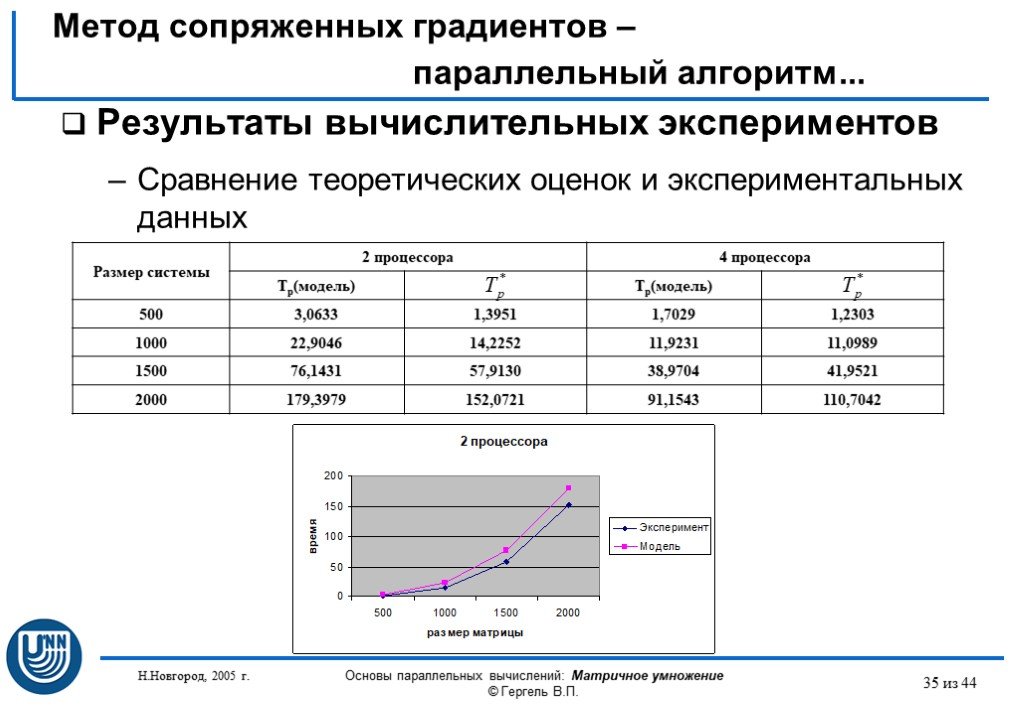
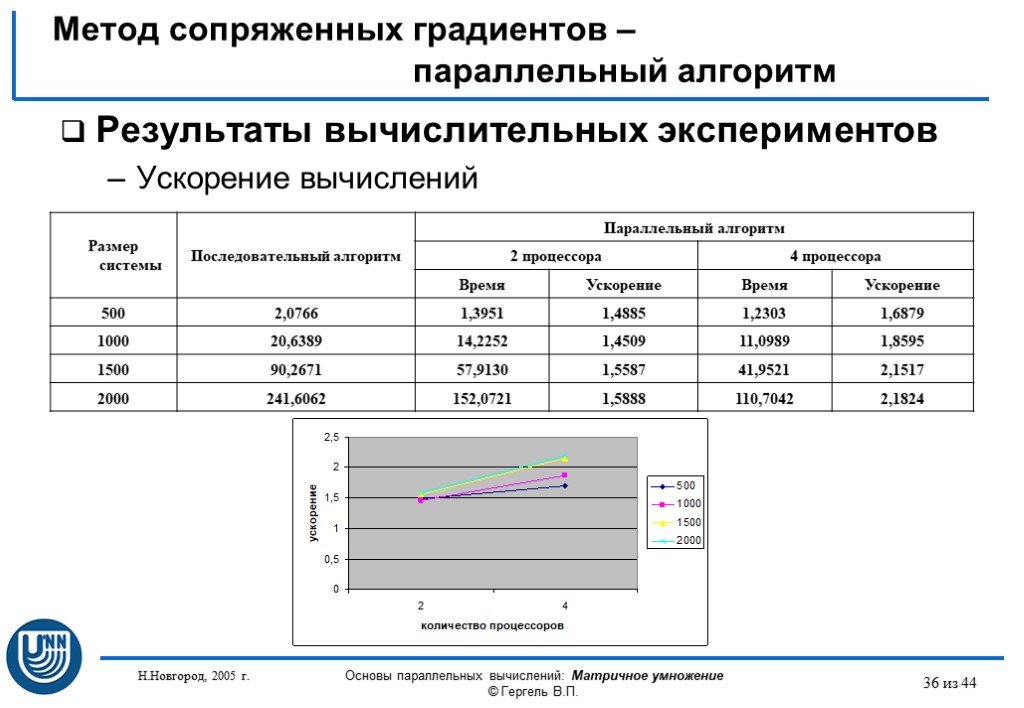
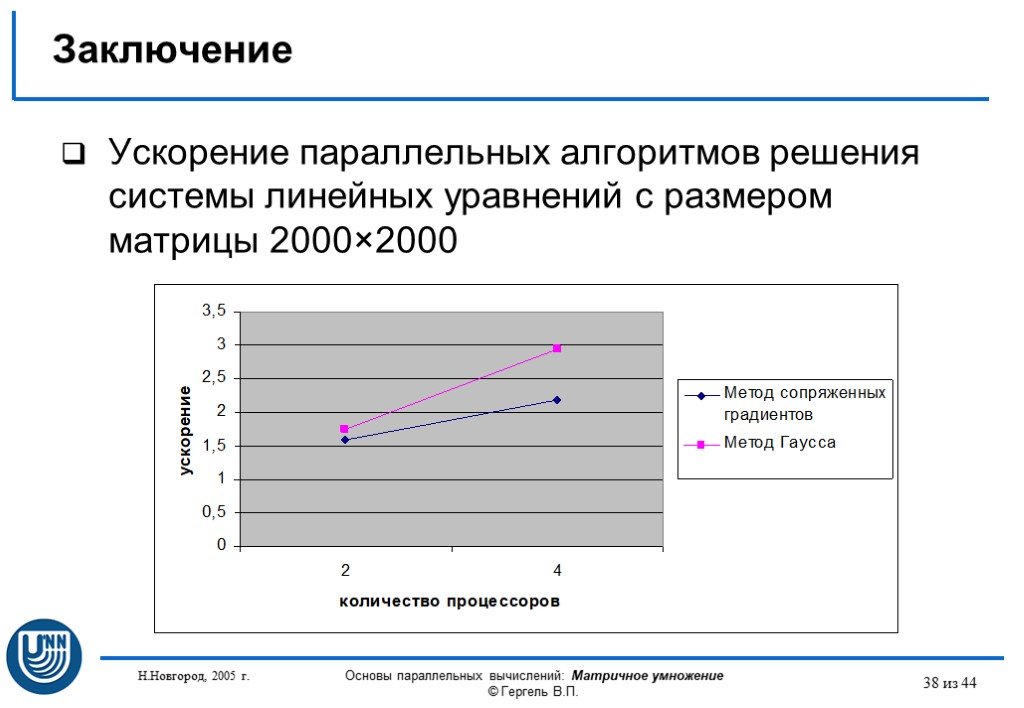
Презентация "Параллельные методы решения систем линейных уравнений" (11 класс) по математике – проект, доклад
Презентацию на тему "Параллельные методы решения систем линейных уравнений" (11 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 44 слайд(ов).
Слайды презентации
Список похожих презентаций
Методы решения систем линейных уравнений с двумя переменными
Инженер-электрик: "Это уравнения напряжения или токов в электрической цепи с активными сопротивлениями." Инженер-строитель: "Это уравнения, связывающие ...Методы решения систем линейных уравнений 1- ой степени
Проверка домашнего задания. Устная работа. Какие способы решения систем линейных уравнений мы знаем? Сколько их? Какой из способов самый наглядный? ...Метод Гаусса решения систем линейных уравнений
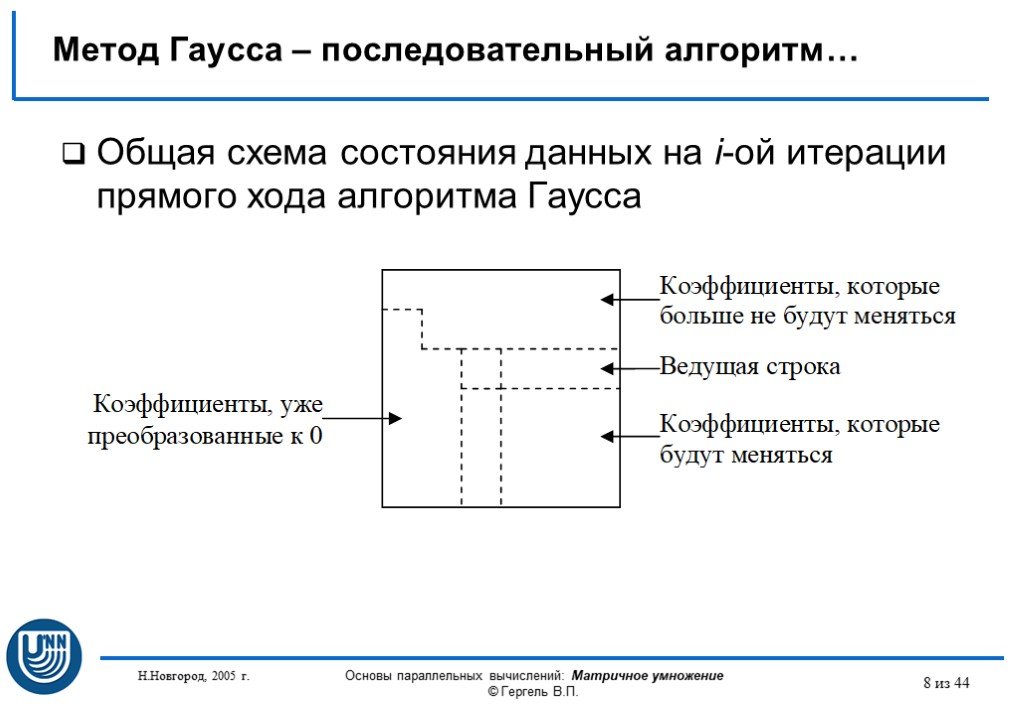
Рассмотрим систему m линейных уравнений с n неизвестными:. Назовем матрицей системы матрицу, составленную из коэффициентов при неизвестных. Матрицу, ...Графический способ решения линейных систем уравнений
Линейная функция – это функция вида y=kx+b , в котором k и b - действительные числа. Графиком линейной функции y=kx+b является прямая. Алгоритм ...Методы решения систем уравнений
Под кейсом понимается несколько страниц текста, материал из учебника, различные презентации, видеоматериал. Ответ:. . . Обратимся к кейсу. Если х=0, ...Аналитический и численный методы решения систем уравнений с параметром
АНАЛИТИЧЕСКИЙ И ЧИСЛЕННЫЙ МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ С ПАРАМЕТРОМ. Астрахарчик Н.А. Система симметрична относительно знака x. Система симметрична ...Методы решения логарифмических уравнений
Цель:. Систематизировать знания учащихся о решении логарифмических уравнений. Сформировать умения решать логарифмические уравнения. Показать возможности ...Автоматизация труда учителя на примере решения систем алгебраических уравнений с использованием программного пакета MATHCAD
Ознакомить учителей математики с возможностями продукта MathCAD Обеспечить автоматизацию работы учителей с использованием MathCAD Рассмотреть решение ...Графический способ решения систем уравнений
Построение графика линейной функции. Прямая линия. y = ах + b. х – любое действительное число. 1. Повторение. Построение графика функции обратной ...Графический метод решения систем уравнений с двумя переменными
Обобщить графический способ решения систем уравнений; Сформировать умения графи-чески решать системы уравне-ний второй степени, привлекая известные ...Методы решения уравнений с одной переменной
Тема урока: «Решение уравнений с одной переменной». Цели урока: закрепить знания и умения решений квадратных уравнений; повторить основные методы ...Методы решения квадратных уравнений
Определение. Квадратные уравнения (КВУР) – уравнения вида ax²+bx+c=0, где x – переменная, a, b и c – любые числа, причем a≠0. (В случае, когда а = ...Методы решения тригонометрических уравнений
ЦЕЛЬ:.Систематизировать, обобщить, расширить знания и умения, связанные с применением методов решения тригонометрических уравнений. . . 1. Какие ...
Аналитические методы решения логарифмических уравнений
Цели урока:. Обобщить и систематизировать изученные методы решения логарифмических уравнений Выявить особенности каждого метода Выяснить, всегда ли ...Методы решения тригонометрических уравнений
Восемь способов решения одного тригонометрического уравнения. 1.Приведение уравнения к однородному. 2.Разложение левой части уравнения на множители. ...Методы решения уравнений
Результат учения равен произведению способности на старательность. Если старательность равна нулю, то и все произведение равно нулю. А способности ...Методы решения уравнений высших степеней
Учитель математики Мурзабаева Фарида Мужавировна. Виды уравнений высших степеней. Уравнения третьей степени. Уравнения четвертой степени. Уравнения ...Методы решения логарифмических уравнений
Задачи урока распределяются по 3 уровня:. 1 уровень – уметь решать простейшие логарифмические уравнения, применяя определение логарифма, свойства ...Методы решения квадратных уравнений
Проверим знания определений, формул и формулировок правил, которые необходимо знать для успешного усвоения темы и умений решать квадратные уравнения. ...Методы решения логарифмических уравнений
Основные методы решений логарифмических уравнений. Определение. Логарифмом положительного числа b по основанию a, где a>0, , называется показатель ...Конспекты
Методы решения систем двух линейных уравнений с двумя переменными
План- конспект урока алгебры в 7 классе по теме: «Методы решения систем двух линейных уравнений с двумя переменными». Орг. момент, сообщение ...Методы решения систем уравнений
МУНИЦИПАЛЬНОЕ КАЗЕННОЕ. . ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ. . «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №5» г.Михайловска. Методическое объединение ...Основные методы решения тригонометрических уравнений
. МАТЕМАТИКА 11 класс. Тема: Основные методы решения тригонометрических уравнений. Цели урока:. Обобщить и систематизировать полученные знания ...Применение метода подстановки для решения систем уравнений
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа города Пионерский». Калининградской области. ...Графический способ решения систем уравнений
Тема урока:. . Графический способ решения систем уравнений. Тип урока. : Урок изучения нового материала. Цели урока. :. Образовательные. ...Графический способ решения систем уравнений
2. . . Дата: ________________. Класс: 9. Предмет: алгебра. Тема: «Графический способ решения систем уравнений». Цели:. Использовать графики ...Графический способ решения систем уравнений
. . . . . . Урок алгебры по теме. «Графический способ решения систем. уравнений». Автор: Гаврилова Ирина Николаевна. Учитель математики ...Графический способ решения систем двух уравнений с двумя неизвестными
ПЛАН-КОНСПЕКТ УРОКА Графический способ решения систем двух уравнений с двумя неизвестными. . ФИО (полностью). . Гудиева Альбина Ахсаровна. ...Графический способ решения систем уравнений
Открытый бинарный урок (алгебра и информатика) по теме:. Графический способ решения систем уравнений. . (9-й класс). Учебник: Алгебра, 9 класс, ...Виды уравнений. Методы решения уравнений
ГАОУ НПО Профессиональный лицей № 59. Оренбургская область, Красногвардейский район, с. Плешаново. Виды уравнений. Методы решения уравнений. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:28 января 2019
Категория:Математика
Классы:
Содержит:44 слайд(ов)
Поделись с друзьями:
Скачать презентацию