Презентация "Квадратное уравнение" по математике – проект, доклад
Презентацию на тему "Квадратное уравнение" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 15 слайд(ов).
Слайды презентации
Список похожих презентаций
Квадратное уравнение. Неполные квадратные уравнения
Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, кто желает к ним приобщиться, должен достигнуть этого собственной ...Квадратное уравнение
Устная работа. Укажите в квадратном уравнении коэффициенты:. 2. Решите неполные квадратные уравнения. Вывод формулы. Решить квадратное уравнение выделением ...Квадратное уравнение и теорема Виета
Цель урока:. Повторить решение квадратных уравнений общего вида, неполных квадратных уравнений. Рассмотреть и доказать теорему Виета и сформулировать ...Квадратное уравнение и его корни
Квадратное уравнение и его корни. 4х=12 1. 2. х = 3х-1=8 Решить уравнение 2х-4=х +1 4. aх+b=0 5. Пусть х – задуманное число.х² + 10х =0. Квадратным ...
Квадратное уравнение
История. Неполные квадратные уравнения и частные виды полных квадратных уравнений умели решать вавилоняне. Об этом свидетельствуют найденные клинописные ...Приведенное квадратное уравнение
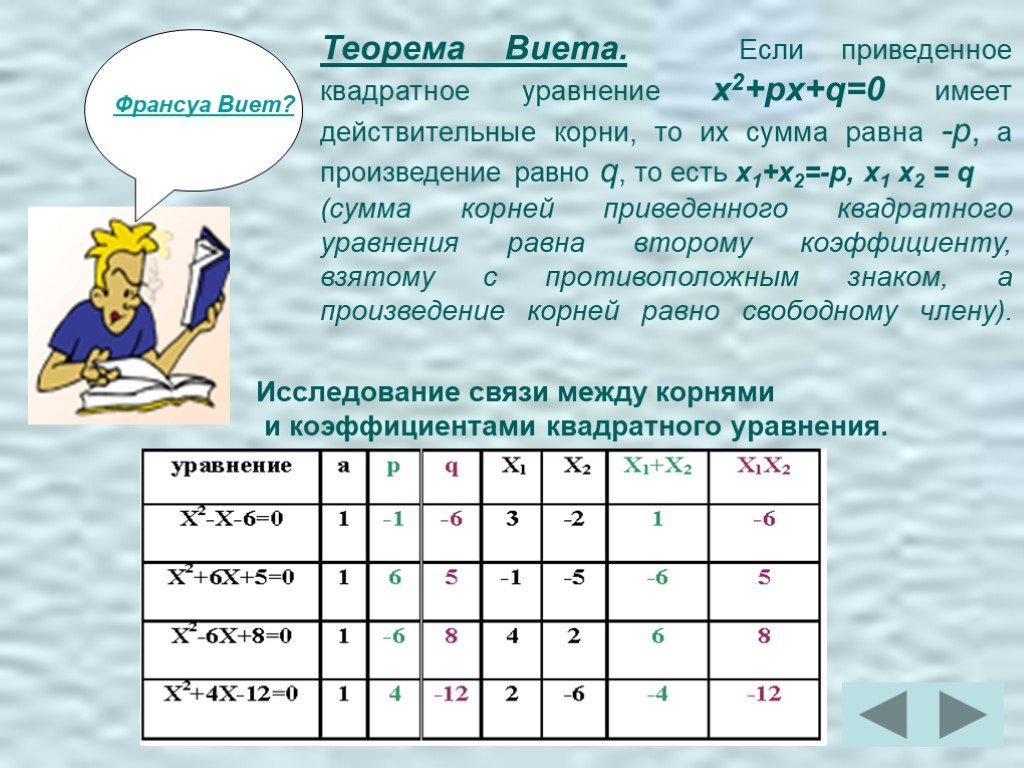
ЗАПОЛНИТЬ ТАБЛИЦУ. . Не решая уравнения, заполни таблицу. . . . Самостоятельная работа. Автор шаблона : Ермолаева Ирина Алексеевна учитель информатики ...Основное уравнение МКТ
Цель урока: Установить взаимосвязь между макроскопическими и микроскопическими параметрами Научиться решать вычислительные задачи с использованием ...Линейное уравнение с одной переменной
Содержание. Определение. Корень уравнения. Решение уравнения. Сколько корней может иметь линейное уравнение. Алгоритм решения линейного уравнения. ...Линейное уравнение с одной переменной
Запомнить. Уравнение вида ax =b, где x - переменная , a и b – некоторые числа, называется линейным уравнением с одной переменной. Найти корень уравнения. ...Целое уравнение и его корни
Определение. Целым уравнением с одной переменной называется уравнение, левая и правая части которого – целые выражения. Например: х²+2х-6=0, х⁴+х⁶ ...Целое уравнение и его корни
2х3-2х2-3х+5=0 Мы привели уравнение к виду Р(х)=0, где Р(х) – многочлен стандартного вида, степень этого многочлена называют степенью уравнения. В ...Линейное уравнение с двумя переменными
Уравнения с одной переменной. Задача 1: Задуманы 2 числа. Обозначив за х первое число, y-второе число, составим соотношение по следующим условиям:. ...Линейное уравнение с двумя переменными
Цели урока:. Ввести определение линейного уравнения с двумя переменными; решения линейного уравнения с двумя переменными; разобрать алгоритм определения ...колобок и уравнение
Цели урока:. решать и составлять простые уравнения и задачи с применением изученных действий с числами переносить и экстраполировать решение некоторых ...Решить уравнение
Неравенства, содержащие модуль. |f(x)|. |f(x)|>a. если a0, то. |f(x)| |g(x)|. |f(x)|. |f(x)|>g(x). |f(x)|+|g(x)|. ...Целое уравнение и его корни
Проверка домашнего задания. Вариант А У4 – у3 – 16у2 + 16у = 0; (у4 – у3) – (16у2 – 16у) = 0; У3(у - 1) – 16у(у - 1) = 0; (у2 – 16у)(у - 1) = 0; у(у ...Линейное уравнение с двумя переменными и его график
Цель: дать понятие об уравнении с двумя переменными, их решении и графике уравнения. 13.02.2019. Повторение материала: Алгоритм нахождения координат ...Целое уравнение и его корни
Цель урока. Повторить пройденный материал Закрепить полученные знания Подготовиться к контрольной работе. Напутствие. "Чтобы спорилось нужное дело, ...Целое уравнение и его корни
Определение. Целым уравнением с одной переменной называется уравнение, левая и правая части которого – целые выражения. Примеры целых уравнений: 0,7х7–3х5–х=5 ...Конспекты
Уравнения, приводимые к квадратным. Биквадратное уравнение
Тема урока: «. Уравнения, приводимые к квадратным. Биквадратное уравнение. Тип урока:. Урок обобщения и закрепления полученных знаний. Цели урока:. ...Биквадратное уравнение и его корни
Учитель математики Апенькина Наталья Александровна. Конспект урока. Класс – 8. Тема – «Биквадратное уравнение и его корни». Цели урока: . образовательная:. ...Что такое уравнение?
Тема:. Что такое уравнение? Цель: формирование понятия «уравнение», «корень уравнения», умения решать уравнения. Ход урока. 1.Мотивация. Прозвенел ...Целое уравнение и его корни
Интегрированный урок (алгебра + английский язык в 9-м классе). Тема: "Целое уравнение и его корни". «. The whole. . equation and its. . roots. ...Решение квадратных уравнение различными способами
МОУ Большеключищенская средняя общеобразовательная школа имени В.Н. Каштанкина. Выполнила: Ушкова Анна Викторовна. учитель математики ...Линейное уравнение с параметром
Урок математики в 7 классе. Тема: « Линейное уравнение с параметром ». Учитель математики МБОУ «СОШ №14». Г.Братск. Жукова Светлана Владимировна. ...Линейное уравнение с одной переменной
Линейное уравнение с одной переменной. 7-й класс. . Бекоева Джулета Хазбиевна. ,. учитель математики. СП МБОУ СОШ №3. Урок . . . Тип ...Линейное уравнение с одной переменной
Конспект урок по теме:. «Линейное уравнение с одной переменной». по. . учебнику алгебры, 7 класс (Макарычев Ю.Н. под ред. Теляковского С.А.). ...Линейное уравнение с одной переменной
Отдел образования администрации Тальменского района Алтайского края. МОУ Новоозёрская средняя общеобразовательная школа. Проект урока ...Линейное уравнение с одной переменной
Похабова Наталья Юрьевна, учитель математики и физики Кальская ООШ. Открытый урок математики в 6 классе - 13.12.2011 год. Тема:. Линейное уравнение ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:19 июня 2019
Категория:Математика
Содержит:15 слайд(ов)
Поделись с друзьями:
Скачать презентацию