Презентация "Движение фигур в стереометрии" по математике – проект, доклад
Презентацию на тему "Движение фигур в стереометрии" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 9 слайд(ов).
Слайды презентации
Список похожих презентаций
Аксиомы стереометрии и их следствия
Цели:. Изучить аксиомы стереометрии: - о взаимном расположении точек, - о взаимном расположении прямых, - о взаимном расположении плоскостей в пространстве. ...Аксиомы стереометрии и их следствия. Решение задач
Цель урока: обобщение и применение аксиом и их следствий к решению задач. Математический диктант. 1). Сформулируйте аксиомы стереометрии: Аксиома ...Аксиомы стереометрии и их простейшие следствия
Аксиомы стереометрии. 1)Какова бы ни была плоскость, существуют точки, принадлежащие ей и точки, не принадлежащие ей. 2) Если две плоскости имеют ...Аксиомы стереометрии Решение задач
Через любые две точки пространства проходит единственная прямая. Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная ..."Симметрия в архитектуре Старого Оскола"
Остановка 1. Главная улица города – улица Ленина. Мы находимся в центре нашего города у здания администрации. Какие приемы использовал архитектор, ...Биография М.В. Ломоносова в цифрах
=2 =0,3 =3,6 =0,04 =1 =0,8 =0,42 =21,2 М И Ш А Н С К О Е. Ломоносов Родился в с. Мишанинском Архангельской губернии. 8 ноября 1711. Длина = 15,5 м ...Без математики, друзья, в жизни нам никак нельзя
Актуальность. Математика находится в тесной связи со всеми естественными, гуманитарными, точными науками и др., математические знания применяются ...Арифметические действия в двоичной системе счисления
ЗАДАНИЕ «ТЕЗИСЫ». Верно ли каждое из следующих утверждений? Если «Да», то записывайте 1. Если «Нет», то записывайте 0. В результате должно получиться ...Арифметическая прогрессия в древности
Египетские папирусы и вавилонские клинописные таблички, относящие ко II тыс. до н.э., содержат примеры задач на арифметическую прогрессию. Каких-либо ...Алгебраические поверхности в пространстве
Цели и задачи. Цели: Рассмотреть основные понятия по теме «Алгебраические поверхности второго порядка в пространстве» Задачи: Рассмотреть понятие ...Аксиомы стереометрии
Повторить аксиомы планиметрии Познакомиться с аксиомами стереометрии Уметь соотносить математическую формулировку аксиомы с графическим изображением ...Аксиомы стереометрии
Содержание:. 1.Понятия стереометрии 2. Изображение плоскости 3.Аксиомы стереометрии 4.Следствия из аксиом стереометрии. Система аксиом стереометрии ...5.Уравнение в полных дифференциалах. Интегрирующий множитель
Теорема:. Для того чтобы дифференцировать выражение , где и определены и непрерывны в области плоскости и имеют в ней непрерывные частные производные ...«Симметрия в пространстве» геометрия
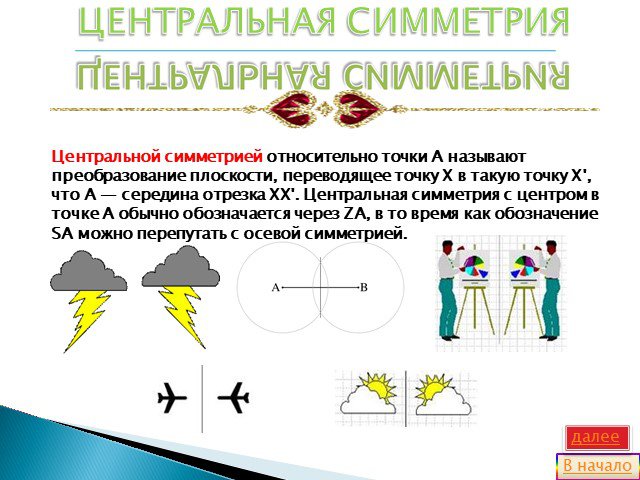
Что такое симметрия? Симметрия в переводе с греческого означает соразмерность. Под симметрией принято понимать свойство геометрической фигуры, расположенной ...«Математика в профессиях»
Ознакомление с типами профессий и характеристиками труда. Исследование значения математики в различных областях деятельности человека. Развитие познавательной ...«Закрепление изученого» (Сложение и вычитание с переходом через десяток в пределах 20)
Цели урока:. 1. Закрепить знания о сложении и вычитании с переходом через десяток в приделах 20. 2. Упражняться в решении задач изученных видов. План ..."Смешанные дроби. Представление смешанного числа в виде неправильной дроби".
Смешанные дроби. Представление смешанного числа в виде неправильной дроби. 02.03. Определите координаты точек А, В, С и М. ...Алгебра в 9 классе.
Функция их свойства и графики. Сформулируйте определение чётной функции, определение нечётной функции. Не является ни чётной, ни нечётной. чётная ...Алгебраические кривые в полярной системе координат и их применение в природе и технике
Цель: познакомиться с кривыми, не изучаемыми в школьном курсе алгебры, найти для них примеры в природе и технике. Локон Аньези. плоская кривая, геометрическое ...Аксиомы стереометрии
ОСНОВНЫЕ ПОНЯТИЯ. Расстояние, точка, прямая, плоскость, Множество. обозначения плоскостей. М – все точки пространства. Аксиома 1. В пространстве существуют ...Конспекты
Виды треугольников. Плоскостное моделирование и конструирование. Аппликация из геометрических фигур — треугольников
Тема. : «Виды треугольников. Плоскостное моделирование и конструирование. Аппликация из геометрических фигур — треугольников». . Цели занятия. ...Виды углов в планиметрии
Лабораторно-практические занятия по геометрии в 7 классе. Лабораторно-практические занятия имеют важное значение, особенно при обучении детей с ...Введение в теорию вероятностей
9 класс. Тема: Введение в теорию вероятностей.(90 мин.). Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, ...Видеть и слышать, или как не потеряться в мире информации
Конспект – сценарий урока, разработанного учителями МОУ Брызгаловская СОШ Ивановой Е.Б. и Колпаковой Л.В. Тема: «Видеть и слышать, или как не потеряться ...Большие и малые числа в химии
МКОУ «Средняя общеобразовательная школва №5. . города Ершова Саратовской области». . Бинарный урок. Большие и малые числа в химии. Провели ...Бородинское сражение в математических задачах
Открытый урок «Бородинское сражение в математических задачах». Карташова Ирина Викторовна , учитель математики МБОУ «Бирюковская СОШ». Техническое ...Арифметический способ отбора корней в тригонометрических уравнениях
Конспект урока для 11 класса на тему «Арифметический способ отбора корней в тригонометрических уравнениях». Цели и задачи урока:. . . повторение ...Аксиомы стереометрии
Тема урока. :. Аксиомы стереометрии. Цель урока:. ♦ рассмотреть пространственные аксиомы С1. – С3. и стереометрические аналоги. планиметрических ...Аксиомы стереометрии
. Дмитрикова Ольга Викторовна. учитель математики. МКОУ "Огорская СОШ". с.Огорь. Жиздринский район. Калужская область. класс 10. ...I признак равенства треугольников в задачах
ТЕМА УРОКА:. I. признак равенства треугольников в задачах. ТИП УРОКА. : закрепление изученного материала. КОНТИНГЕНТ УЧАЩИХСЯ:. 7 класс. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 января 2015
Категория:Математика
Содержит:9 слайд(ов)
Поделись с друзьями:
Скачать презентацию