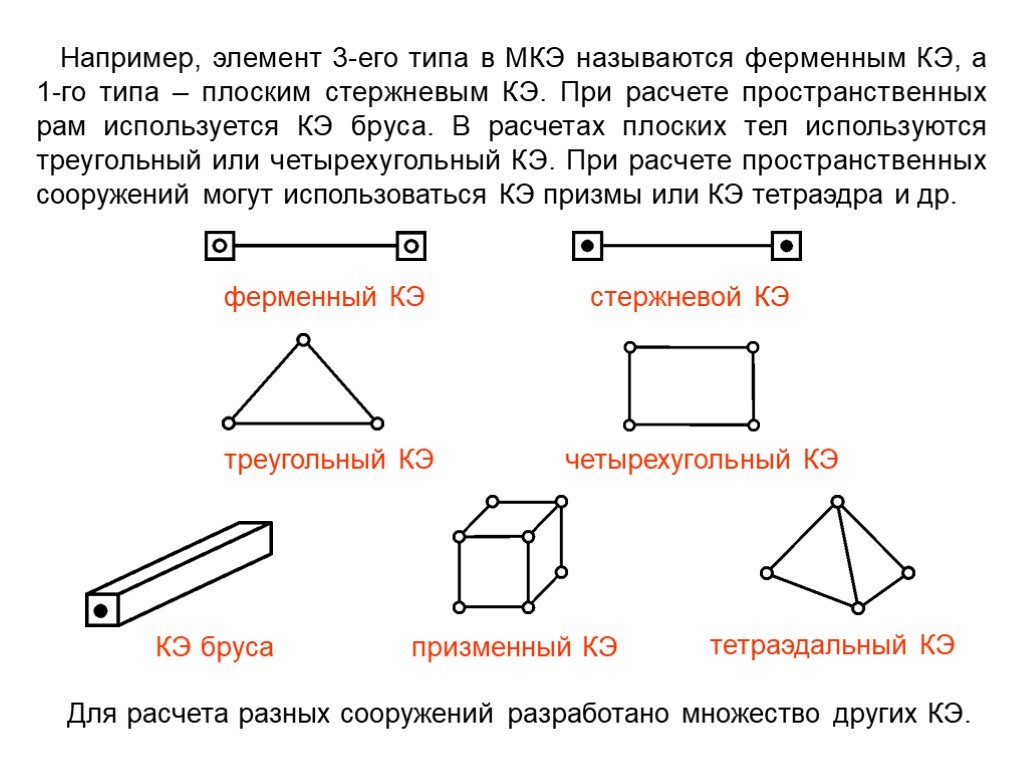
Презентация "Расчет сооружений методом конечных элементов" по математике – проект, доклад
Презентацию на тему "Расчет сооружений методом конечных элементов" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 15 слайд(ов).
Слайды презентации
Список похожих презентаций
Решение неравенств методом интервалов
Треугольник. символизирует лидерство. Самой характерной особенностью человека, выбравшего этот символ, является концентрироваться на главной цели. ...Использование элементов технологии самосовершенствования личности на уроках математики в классах коррекционно – компенсирующего обучения
По данным НИИ детства, ежегодно рождается 5 - 8℅ детей с наследственной патологией, 8 – 10 % имеют выраженную врождённую или приобретенную патологию, ...Решение неравенств методом интервалов
Методом интервалов можно решать неравенства вида: f(х)>0 , f(х)0 f(х). Необходимым условием смены знака в точке С является : f (c)=0. Однако , это ...Решение тригонометрических уравнений методом оценки
Не все тригонометрические уравнения можно решить известными нам методами (методами разложения на множители, методами замены переменной или подстановки, ...Стратегия игры. Решение задач методом «ГРАФЫ»
Состав графа. Граф состоит из вершин, связанных линиями. Направленная линия (со стрелкой) называется дугой. Линия ненаправленная (без стрелки) называется ...Решение неравенств с параметрами методом областей
«Но когда эти науки (алгебра и геометрия) объединились, они энергично поддержали друг друга и быстро зашагали к совершенству». Ж.А. Лагранж. АКТУАЛЬНОСТЬ ...Решение системы линейных уравнений методом Крамера
Системы линейных уравнений. Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных. ...Применение элементов математического анализа при решении задач
- Учиться проводить анализ условия задачи, что помогает поиску способа решения;. Цели урока. - Учиться переводить язык задачи на язык производной ...Размещение элементов
Размещение. В комбинаторике размещением называется расположение «предметов» на некоторых «местах» при условии, что каждое место занято в точности ...Построение графика функции методом ее исследования с помощью производной
доцент кафедры математического образования Батан Любовь Федоровна. учитель математики первой квалификационной категории МОУ лицей № 176 Ткаченко Зоя ...Построение сечений многогранников методом «следа»
Секущей плоскостью многогранника называется такая плоскость, по обе стороны от которой есть точки данного многогранника. Сечением многогранника называется ...Построение геометрических фракталов методом рекурсии
"Почему геометрию часто называют холодной и сухой? Одна из причин заключается в её неспособности описать форму облака, горы, дерева или берега моря. ...Моделирование, алгоритмизация и оптимизация элементов и систем в теплоэнергетике
Программа дисциплины Объем: 150 часов Структура: Введение Гл. 1 Методологические основы математического моделирования Гл. 2 Моделирование задач с ...Методика изучения элементов комбинаторики в условиях профильного обучения математике
Содержание. Введение Глава 1. Цели изучения стохастической линии в школе 1) Из истории комбинаторики 2) Цели изучения стохастики в школе Глава 2. ...Решение неравенств методом интервалов
Цели урока:. Закрепление навыков решения неравенств методом интервалов Развитие умений сравнивать решения, выявлять правильные ответы, преодолевать ...Расчет параметров слоев
[Ом·см]. [Ом/]. N(hслоя) = Nподл, N(hслоя) = Nэпитакс. Nэмиттера(h эмиттера) = Nакт базы(h эмиттера). Диффузия в полуограниченную область. Случай ...Решение неравенств методом интервалов
0 x y. Пусть графиком функции y=f(x) является некоторая гладкая кривая:. y=f(x). Очевидно, что D(f)=E(f)=. Обратим свое внимание на значения аргумента ...Расчет погрешностей косвенных измерений
В большинстве случаев измерение физических величин являются косвенными, т.е. результат определяется на основе расчетов. Например, для определения ...Решение систем уравнений методом новой переменной
Решение систем уравнений. методом введения новой переменной переменной. Разминка! Что такое решение системы уравнений? Какие методы решения систем ...Расчет пути и времени движения
t. Схема для запоминания формул расчёта v, t, S при равномерном движении. Запомни! s. Какие единицы скорости вы знаете? 2. Скорость зайца 15 м/с, ...Конспекты
Уравнение. Решение уравнений методом подбора
Тема урока:. «Уравнение. Решение уравнений методом подбора». Класс. -2. . . Тип урока:. закрепления полученных знаний. Предмет -. математика. ...Решение уравнений методом подстановки
Открытый урок по теме:. . . Решение уравнений методом подстановки. . . Учитель математики ГОУ гимназии № 1549 Шмелева Ирина Дмитриевна. ...Уравнение. Решение уравнений методом подбора
Конспект урока математики. 2 класс. Тема:. «Уравнение. Решение уравнений методом подбора». Цель:. Формирование. . представления об уравнении ...Решение неравенств методом интервалов
Тема урока «Решение неравенств методом интервалов». Цель урока. : формировать навыки и умения учащихся при решение неравенств методом интервалов; ...Решение систем уравнений второй степени методом замены переменной
Открытый урок по теме. «Решение систем уравнений второй степени методом замены переменной». Цели урока:. 1) Открыть совместно с учащимися новый ...Решение неравенств методом интервалов
Тема урока:. Решение неравенств методом интервалов. Класс:. 9. . Тип урока:. урок освоения новых знаний. . Цель:. сформировать навыки решения ...Решение неравенств методом интервалов
ПЛАН-КОНСПЕКТ УРОКА Решение неравенств методом интервалов. . ФИО: Метельская Т.А. . . . . Место работы : МОУ Лицей №7 г. Саяногорска. ...Решение квадратных неравенств методом интервалов
Урок 81. 6. Решение квадратных неравенств методом интервалов. учитель математики. СШ №19, г. Актобе Испимбетова А.Т. Цель урока. : Проверить умение ...Особые приёмы при решении трансцендентных неравенств методом интервалов
Павлюк Ирина Владиславовна. учитель математики. МБОУ гимназия №19 г. Липецка. Методическая разработка. «Особые приёмы при решении трансцендентных ...Знакомство с уравнениями. Решение уравнений методом подбора
Урок математики во 2 классе. Тема: Знакомство с уравнениями. Решение уравнений методом подбора. Цели урока:. . Обучающие:. открыть вместе ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 мая 2019
Категория:Математика
Содержит:15 слайд(ов)
Поделись с друзьями:
Скачать презентацию