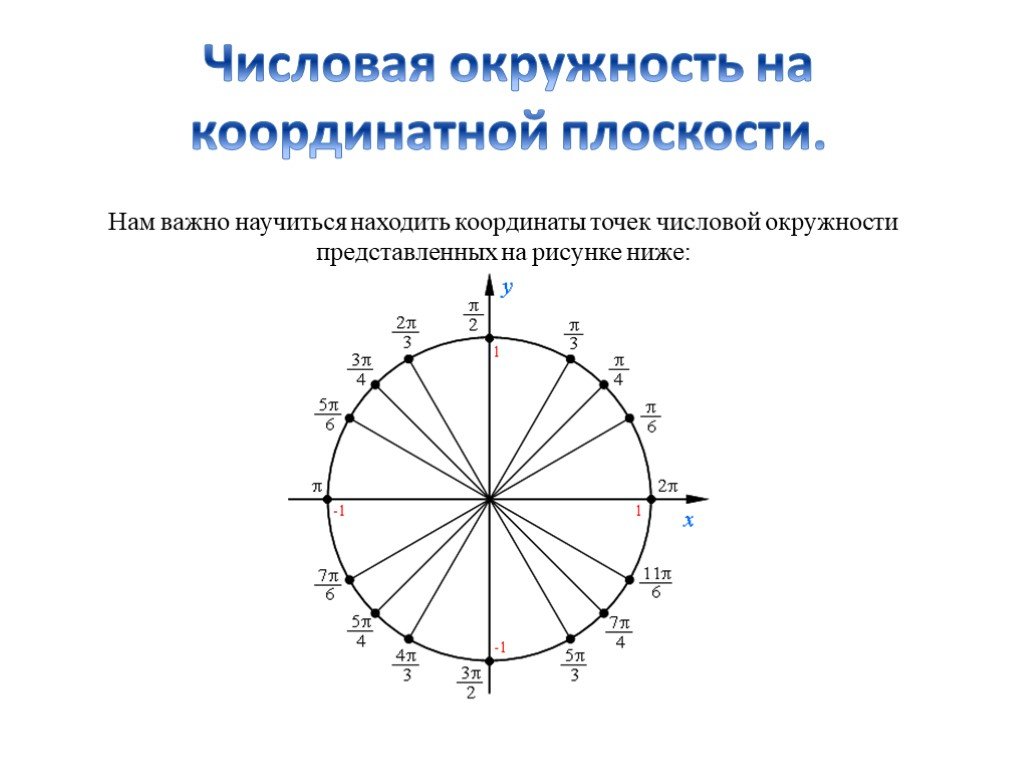
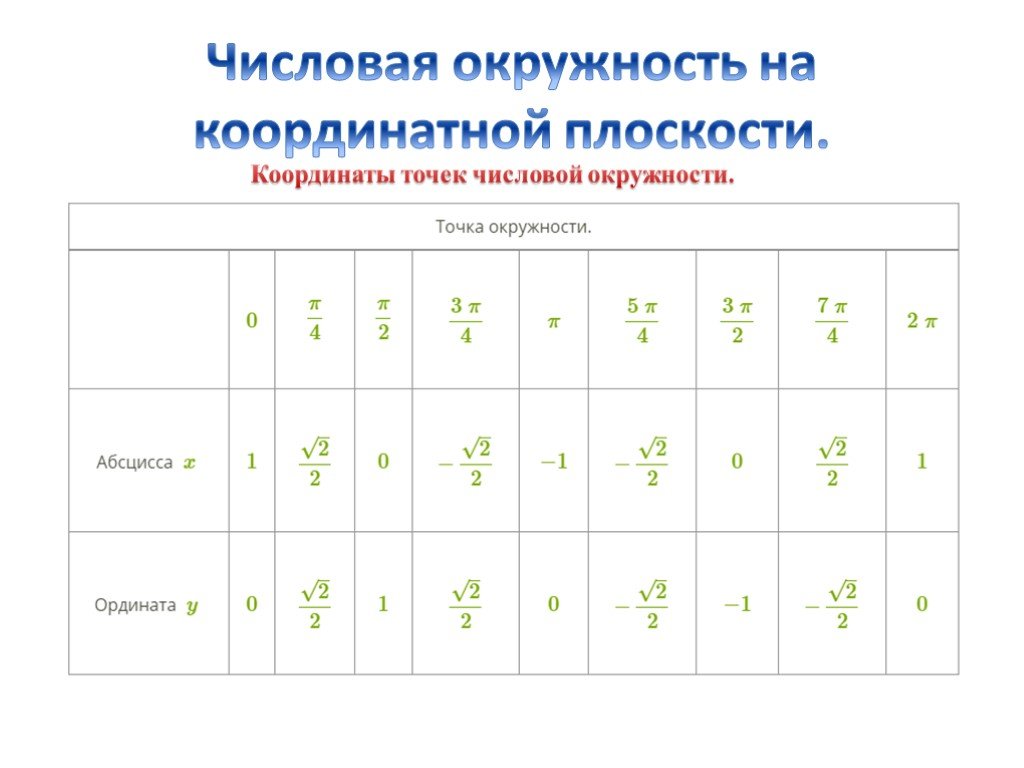
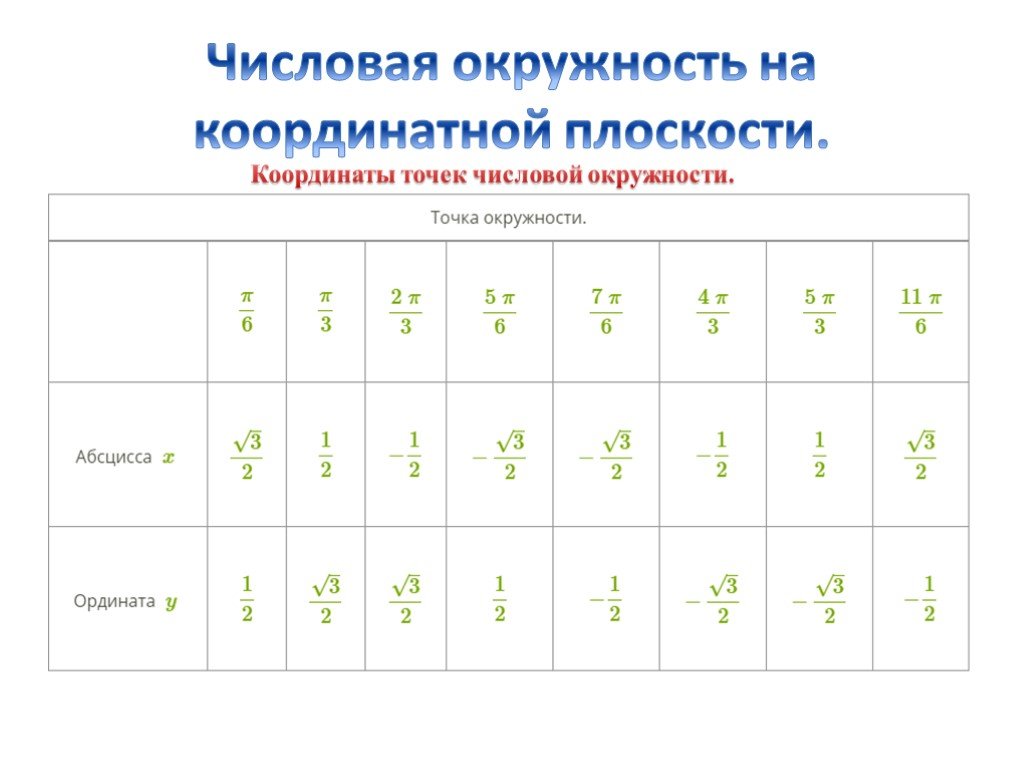
Презентация "Числовая окружность на координатной плоскости." (10 класс) по математике – проект, доклад

Занимательная математика

Алгебра и начала математического анализа, 10 класс.

Урок на тему: Числовая окружность на координатной плоскости.

Числовая окружность на координатной плоскости.

Что будем изучать:

Определение.

Важные координаты числовой окружности.

Как искать координату числовой окружности?

Таблица основных координат числовой окружности.

Примеры задач.

Расположим числовую окружность в координатной плоскости так, чтобы центр окружности совместился с началом координат, а её радиус принимаем за единичный отрезок. Начальная точка числовой окружности A совмещена с точкой (1;0).

Каждая точка числовой окружности имеет в координатной плоскости свои координаты х и у, причем: x > 0, у > 0 в первой четверти; х 0 во второй четверти; х 0, у

Для любой точки М(х; у) числовой окружности выполняются неравенства -1 Запомните!

уравнение числовой окружности:

Нам важно научиться находить координаты точек числовой окружности представленных на рисунке ниже:

Найдем координату точки π/4:

Точка М(π/4) — середина первой четверти. Опустим из точки М перпендикуляр МР на прямую ОА и рассмотрим треугольник OMP.Так как дуга АМ составляет половину дуги АВ, то ∡MOP=45° Значит, треугольник OMP - равнобедренный прямоугольный треугольник и OP=MP, т.е. у точки M абсцисса и ордината равны: x = y Так как координаты точки M(х;y) удовлетворяют уравнению числовой окружности, то для их нахождения нужно решить систему уравнений:

Решив данную систему получаем:

Получили, что координаты точки M, соответствующей числу π/4 будут

Аналогичным образом рассчитываются координаты точек представленных на предыдущем слайде.

Координаты точек числовой окружности.

Пример

Найти координату точки числовой окружности: Р(45π/4)

Решение:

Т.к. числам t и t+2π•k (k-целое число) соответствует одна и тоже точка числовой окружности то: 45π/4 = (10 + 5/4) • π = 10π +5π/4 = 5π/4 + 2π•5

Значит, числу 45π/4 соответствует та же точка числовой окружности, что и числу 5π/4. Посмотрев значение точки 5π/4 в таблице получаем:

Найти координату точки числовой окружности: Р(-37π/3)

Т.к. числам t и t+2π•k (k-целое число) соответствует одна и тоже точка числовой окружности то: -37π/3 = -(12 + 1/3) • π = -12π –π/3 = -π/3 + 2π•(-6)

Значит, числу -37π/3 соответствует та же точка числовой окружности, что и числу –π/3, а числу –π/3 соответствует та же точка что и 5π/3. Посмотрев значение точки 5π/3 в таблице получаем:

Найти на числовой окружности точки с ординатой у = 1/2 и записать, каким числам t они соответствуют.

Прямая у = 1/2 пересекает числовую окружность в точках М и Р. Точка М соответствует числу π/6 (из данных таблицы) значит, и любому числу вида π/6 +2π •k . Точка Р соответствует числу 5π/6, а значит, и любому числу вида 5π/6 +2 π •k Получили, как часто говорят в таких случаях, две серии значений: π/6 +2 π •k и 5π/6 +2 π •k Ответ : t= π/6 +2 π •k и t= 5π/6 +2 π •k

Найти на числовой окружности точки с абсциссой x≥ и записать, каким числам t они соответствуют.

Прямая x = 1/2 пересекает числовую окружность в точках М и Р. Неравенству x ≥ соответствуют точки дуги РМ. Точка М соответствует числу 3π/4 (из данных таблицы) значит, и любому числу вида -3π/4 +2π•k . Точка Р соответствует числу -3π/4, а значит, и любому числу вида – -3π/4 +2 π •k Тогда получим -3π/4 +2 π •k ≤t≤3π/4 +2 π •k Ответ : -3π/4 +2 π •k ≤t≤3π/4 +2 π •k

Задачи для самостоятельного решения.

1) Найти координату точки числовой окружности: Р(61π/6)?

2) Найти координату точки числовой окружности: Р(-52π/3)

3) Найти на числовой окружности точки с ординатой у = -1/2 и записать, каким числам t они соответствуют.

4) Найти на числовой окружности точки с ординатой у ≥ -1/2 и записать, каким числам t они соответствуют.

5)Найти на числовой окружности точки с абсциссой x≥ и записать, каким числам t они соответствуют.