Презентация "Вписанная окружность" по математике – проект, доклад

Скачать презентацию (0.1 Мб) Смотреть похожие презентации Конспекты для презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Презентацию на тему "Вписанная окружность" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 8 слайд(ов).

Скачать презентацию (0.1 Мб) Смотреть похожие презентации Конспекты для презентации

Слайды презентации

Слайд 1

Тема урока:

Вписанная окружность.

Слайд 2

Цели урока:

1.Познакомится с определением вписанной окружности. 2.Изучить доказательство теоремы о вписанной окружности. 3.Решение задач по данной теме.

Слайд 3

Устная работа O M K N

Д а н о: MO = √ 3 МК = 3 Н а й т и:  МКN-? MN-?

B C A

Д а н о:  OAC=20º  АOC=120º Н а й т и: Углы ∆ АBC

Слайд 4

Так четырехугольник EFNM описан около окружности, а четырехугольник NMКD не является описанным около этой окружности.

Если все стороны многоугольника касаются окружности , то окружность называется в п и с а н н о й в многоугольник , а многоугольник – о п и с а н н ы м около этой окружности.

E F D

Слайд 5

В любой треугольник можно вписать окружность.

Т е о р е м а

Слайд 6

Д а н о: ∆ ABC

Д о к а з а т е л ь с т в о: в треугольнике ABC, О – точка пересечения биссектрис.

OK ┴ AС, OL ┴ BC, OM ┴ AB

Стороны ∆ ABC касаются окружности в точках. Значит , окружность с центром О радиуса ОК является вписанной в треугольник АВС.

Что и требовалось доказать

А В С О К L

OK = OL = OM, значит через точки K,M,L проходит окружность

Слайд 7

№ 701.

Слайд 8

Домашняя работа :

1. Что называется вписанной окружностью? 2. Что является центром вписанной окружности? 3. В любой ли треугольник можно вписать окружность?

Вопросы для повторения:

Пункт 74 (теорема) № 690 , №691

Список похожих презентаций

Треугольник. Вписанная окружность

Треугольник. Описанная окружность. Центр описанной окружности – точка пересечения серединных перпендикуляров к сторонам треугольника. 2) Центр описанной ...

Вневписанная окружность треугольника

Вневписанная окружность. B A C Ka K1. Kb Kc ra rb rc. Определение. Вневписанной окружностью треугольника называется окружность, касающаяся одной из ...

Вписанная и описанная окружность

АРХИМЕД (287-212 ДО Н.Э.) – древнегреческий математик и механик. Древние математики не владели понятиями математического анализа. Однако они умели ...

Вписанная и описанная окружность

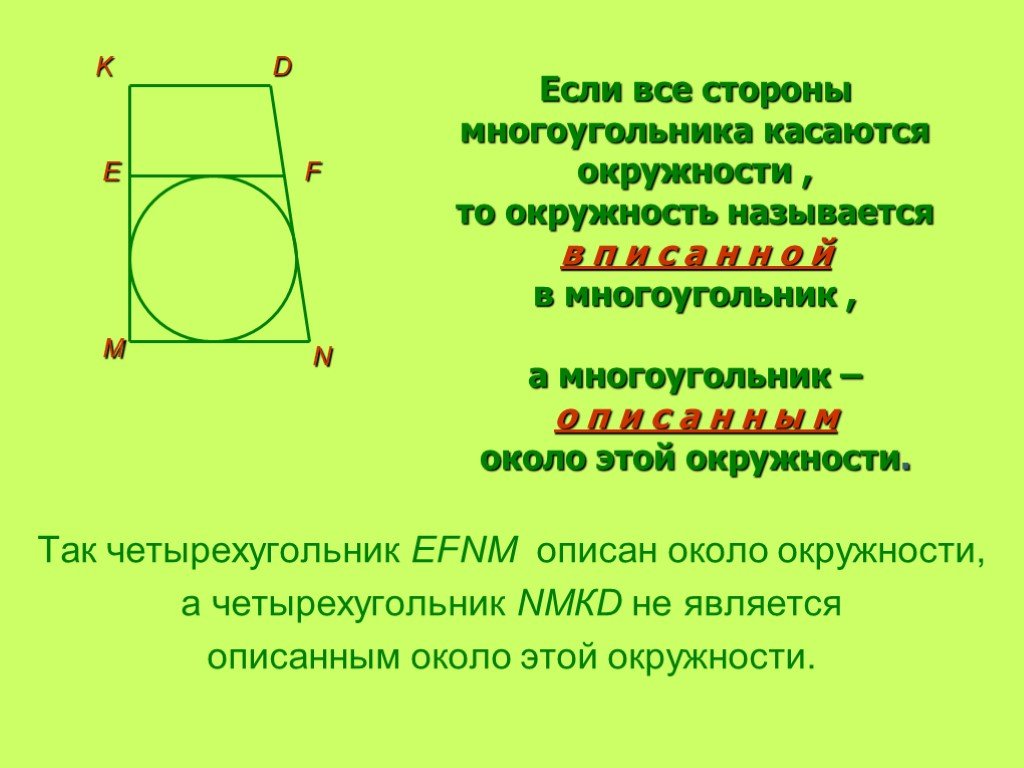
Окружность называется вписанной в многоугольник, если. все стороны многоугольника касаются данной окружности. Всегда ли можно вписать окружность в ...

Вписанная и описанная окружность

1. Окружность с центром в точке О описана около прямоугольного треугольника. Докажите, что точка О -середина гипотенузы. 2. Найдите радиус этой окружности, ...

Вписанная и описанная окружность

ТЕМА: «ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ». ОБРАЗОВАТЕЛЬНАЯ ЦЕЛЬ: ВЫЯСНИТЬ КАК УЧАЩИЕСЯ УСВОИЛИ СВОЙСТВА ВПИСАННОЙ И ОПИСАННОЙ ОКРУЖНОСТЕЙ; ЗАКРЕПЛЕНИЕ ...

Вписанная и описанная окружность

Вписанная окружность. Центр вписанной окружности – середина серединного перпендикуляра к основаниям Если О- центр вписанной окружности, то СОD =90. ...

Вневписанная окружность

Содержание. Введение. Основная часть Глава 1. Определение вневписанной окружности. Центр вневписанной окружности. Касательная к вневписанной окружности. ...

Углы, вписанные в окружность

Углы, вписанные в окружность. Презентацию подготовила учитель математики МОУ Поназыревская СОШ Орлова Н.В. Плоский угол. Это часть плоскости, ограниченная ...

Углы и окружность

Центральные углы Вписанные углы Другие углы. ЦЕНТРАЛЬНЫЕ УГЛЫ. Центральный угол равен градусной мере дуги, на которую он опирается. AOB=AB. OA = ...

Описанная окружность

. . Как вписать \ описать нам окружность счастья? В любую ли фигуру можно вписать окружность? Около какой фигуры можно описать окружность? Вписанная ...

Числовая окружность на координатной плоскости.

Числовая окружность на координатной плоскости. Что будем изучать:. Определение. Важные координаты числовой окружности. Как искать координату числовой ...

Числовая окружность

Назовите числа t, соответствующие точкам на числовой окружности. С А В 0 D. Числовая окружность разделена точками на 12 равных частей. ? Обход окружности ...

Задачи на вписанную окружность

Математический К В Н. Вписанная окружность. Определение: Если все стороны многоугольника касаются окружности, то окружность называется вписанной в ...

Единичная окружность

Окружность радиусом 1 см. 1 см О D С В А Длина окружности:. Длина половины окружности (АС):. Длина четверти окружности (АВ, ВС, СD, DA):. I II III ...

Угол вписанный в окружность

Центральным уголом в окружности называется плоский угол с вершиной в её центре. Угол, вершина которого лежит на окружности, а стороны пересекают эту ...

Центральные углы и углы, вписанные в окружность

Центральный угол. Это угол с вершиной в центре окружности. О. Дуга окружности, соответствующая центральному углу. Это часть окружности, расположенная ...

Задачи на окружность

Цели урока:. Повторить понятия: окружности и круга центра окружности радиуса окружности диаметра окружности Вывести соотношения между радиусом и диаметром. ...

числовая окружность на координатной плоскости

Содержание:. Числовая окружность. Числовая окружность на координатной плоскости Синус и косинус. Тангенс и котангенс. Тригонометрические функции числового ...

Круг и окружность

Цель работы. исследование зависимости между радиусом, длиной окружности и площадью круга. Где используются круги Круги используются в колёсах машин, ...

Конспекты

Советы как сделать хороший доклад презентации или проекта

Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
Старайтесь говорить уверенно, плавно и связно.
Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.