Презентация "Удивительные кривые линии Секция прикладной математики" по математике – проект, доклад
Презентацию на тему "Удивительные кривые линии Секция прикладной математики" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 24 слайд(ов).
Слайды презентации
Список похожих презентаций
Астрономические координаты. Секция: математики
Целью моей работы является нахождение и анализ необходимой информации по данной теме. Задачей является детальное рассмотрение сфер применения на практике ...Введение вероятностно-статистической линии в школьный курс математики
Обязательный минимум содержания образовательных программ. Элементы логики, комбинаторики, статистики и теории вероятностей. Доказательство. Определения, ...Помощь математики в ремонте
План моей комнаты. Измерения для расчетов. Пол (закупка ламината). Размер доски ламината: 1285 x 210 x 12 мм (6 досок в упаковке) Расчеты: - найдем ...Открытый урок математики в 5 классе
Ребята, помогите ответить на вопросы. Как помочь трем поросятам разделить яблоко поровну? Прочитайте дроби 5 6 7 8. 1. Как называется число 5 в записи. ...Неделя математики как способ активизации познавательной деятельности учащихся
развитие личностных качеств обучающихся и активизация их мыслительной деятельности; поддержка и развитие творческих способностей и интереса к предмету; ...Методическая разработка интегрированного урока математики и информатики для учащихся 6 класса "Его величество ПИ"
«СУНДУЧОК ЗНАНИЙ». О С В А. ОА – радиус окружности. r d. ВС – диаметр окружности. ХРАНЕНИЕ ПЕРЕДАЧА ОБРАБОТКА ОБЩЕНИЕ. «СЧЁТНАЯ МАШИНА». «ТВОРЧЕСКАЯ ...Линия уравнений и неравенств школьного курса математики
План. Общие подходы к изучению уравнений и неравенств Формирование представлений об общих методах уравнений Метод уравнений и неравенств в обучении ...Решение уравнений «В мире звезд» Урок математики в 6 классе
1 5 3 6 7 4. Задание № 1 Какое равенство называется уравнение? Какое число называться корнем уравнения? Что значит решить уравнение? Прочитать правило ...Путешествие в страну Занимательной математики
Цели урока:. Закрепим знания сложения и вычитания чисел в пределах 10. Закрепим умения сравнивать числа, решать задачи. Сосчитай-ка. 2 6 7 9 4. Загадай-ка. ...Ассоциация, как помощник, при изучении математики
Ассоциация- это мысленная связь между двумя образами. Чем многообразнее и многочисленнее ассоциации, тем прочнее они закрепляются в памяти. Странные, ...Алгебраические кривые в полярной системе координат и их применение в природе и технике
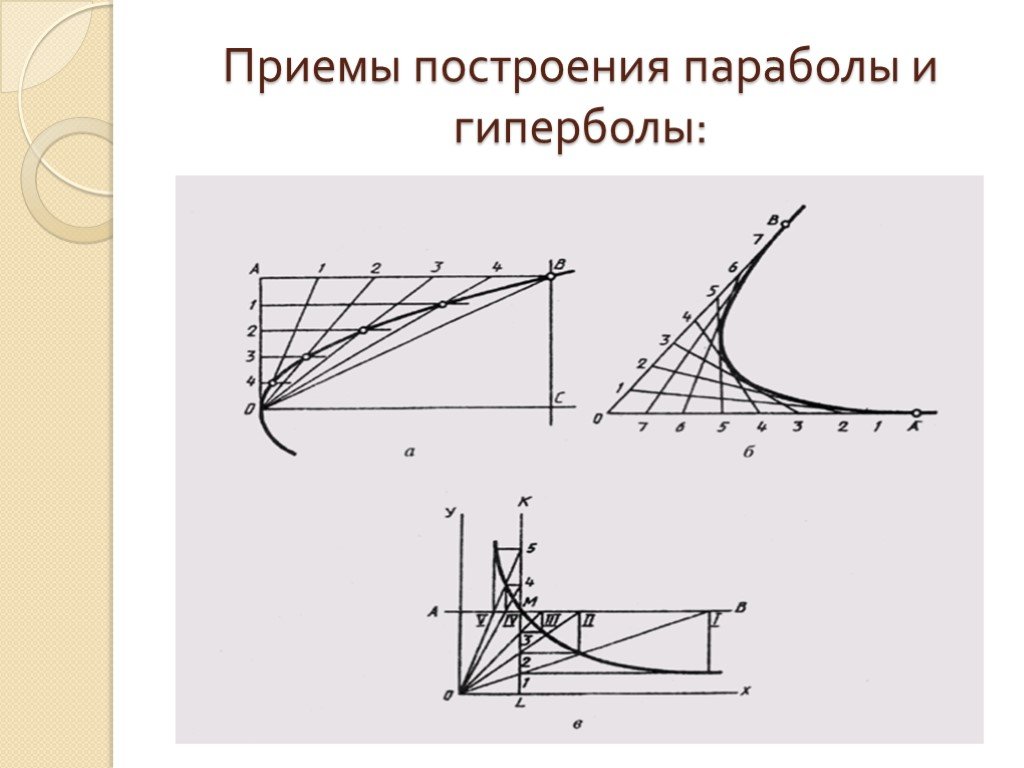
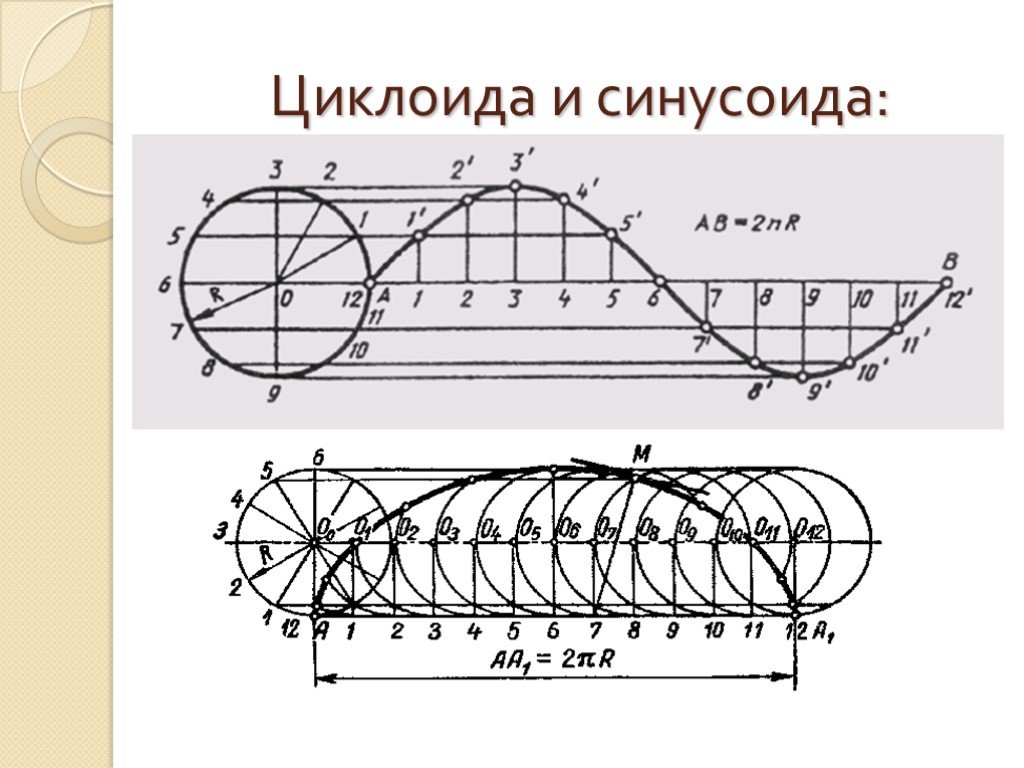
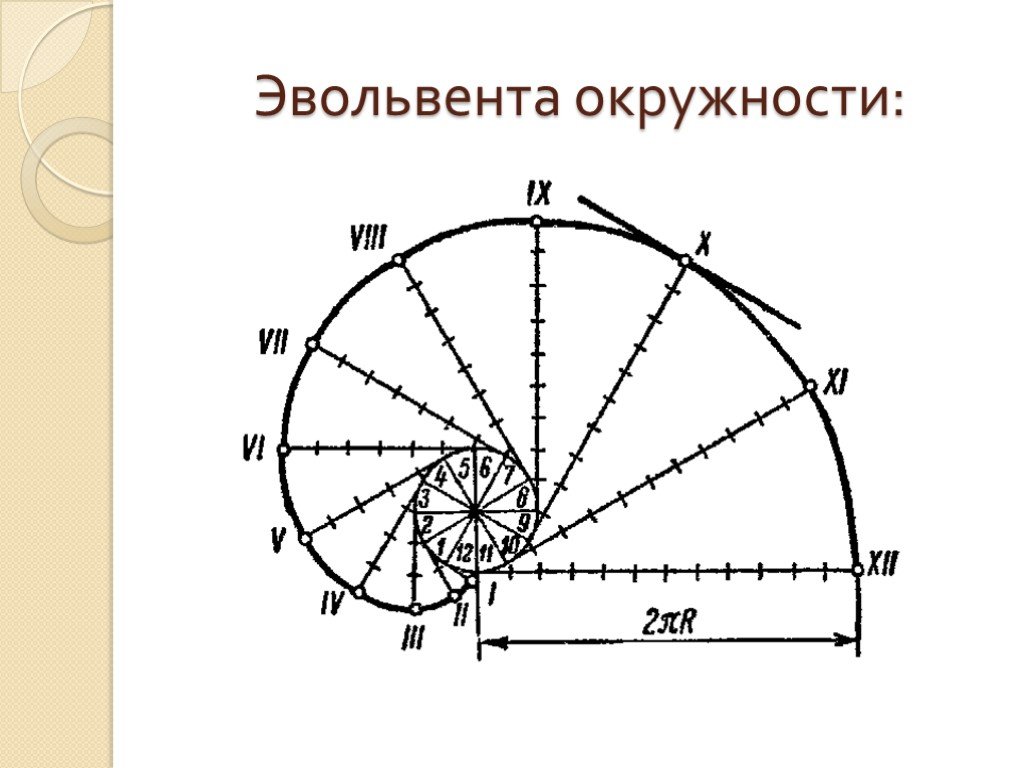
Цель: познакомиться с кривыми, не изучаемыми в школьном курсе алгебры, найти для них примеры в природе и технике. Локон Аньези. плоская кривая, геометрическое ...Активные методы обучения на уроках математики и во внеурочной деятельности
Активные методы обучения — это методы, которые побуждают учащихся к активной мыслительной и практической деятельности в процессе овладения учебным ...Активизация мыслительной деятельности на уроках математики
Активные формы урока. Урок-лекция. Урок-консультация. Урок-практикум Урок-семинар Урок-зачёт. урок-лекция. Зачёт №2 по геометрии в 11 классе 1.Объясните, ...Авторалли по городам математики
Цель: Закрепить навык выполнения действий, возведения чисел в квадрат и куб, закрепить формулы пути и площади. Расширение кругозора учащихся, развитие ...Приемы рефлексии на уроках математики
Рефлексия – размышление человека, направленное на анализ самого себя (самоанализ) – собственных состояний, своих поступков и прошедших событий. Определение. ...Проблемные ситуации на уроках математики
1.Через умышленно допущенные учителем ошибки. 2.Через использование занимательных заданий. 3.Через решение задач, связанных с жизнью. 4.Через выполнение ...Без математики, друзья, в жизни нам никак нельзя
Актуальность. Математика находится в тесной связи со всеми естественными, гуманитарными, точными науками и др., математические знания применяются ...Развитие математики на Руси
Алфавитное обозначение чисел кириллицей. 1136г.- «Кирика диакона и доместика Новгородского Антониева монастыря». Денежные меры. рубль = 2 полтинам ...Бинарный урок математики и природоведения по теме "Итоговое повторение"
Итоговое повторение. Ну-ка, проверь дружок, Ты готов начать урок? Всё ль на месте, Всё ль в порядке, Ручка, книжка и тетрадка? Все ли правильно сидят? ...Связь музыки и математики
Настоящая наука и настоящая музыка требует однородного мыслительного процесса. А Энштейн. Существует распространенное мнение, что Математика и Музыка ...Конспекты
Школьные экологические проблемы на уроке математики
Интегрированный урок (математика + экология) в 5-м классе по теме "Школьные экологические проблемы на уроке математики". Цели:. математика:. ...Урок математики для 4 класса
«Хочется, чтобы дети были. путешественниками, открывателями. и творцами в этом мире». ( В.А. Сухомлинский). Проблема познавательного интереса ...Формирование познавательных процессов на уроках математики
Кировское областное государственное общеобразовательное автономное учреждение средняя общеобразовательная школа г. Лузы. . ...Точка. Прямая и кривая линии
УМК «Гармония» 1 класс. Тема:. «Точка. Прямая и кривая линии. ». Автор: Хохлова Ирина Борисовна, учитель. . начальных классов. МБОУ ...Урок математики 3 класс: Что узнали. Чему научились. Как до 1000 докатились
Хочу с проектом урока познакомить вас. Урок математики - 3 класс. Направление – ФГОС. . . Чему научатся и могут научиться, вот в чем вопрос. ...Самые важные понятия математики
Интегрированный урок (математика + история). в 5 классе по. теме «Самые важные понятия математики». Л.Н. Головина, учитель математики. Заречненской ...Страна математики
Конспект итогового занятия в второй младшей группе. . . . Хасимова Чулпан Максумзяновна. Воспитатель МБДОУ № 76. . Республики Татарстан, ...Знатоки математики
Математическая игра. . «Знатоки математики». 10 класс. Подгорнова Людмила Игнатьевна. МАОУ СОШ №38 г.Златоуст. Учитель математики. ...Из истории математики
Урок математики в 5 классе. «Из истории математики». . . При проведении урока необходимо иметь карту, на которой обозначены Греция, Египет Россия, ...Великие математики России. С.В. Ковалевская
План-конспект внеклассного мероприятия. «Великие математики России. С.В. Ковалевская». . ФИО. . Ракитина Эльвира Альбертовна. . ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:12 августа 2019
Категория:Математика
Содержит:24 слайд(ов)
Поделись с друзьями:
Скачать презентацию

























![Дезарг Жерар [1593, Лион, — 1662, там же (по др. данным — 1591—1661)], французский математик. Был военным инженером. Заложил основы проективной и начертательной геометрии. В своих исследованиях систематически применял перспективное изображение. Первым ввёл в геометрию Бесконечно удалённые элементы. Дезарг Жерар [1593, Лион, — 1662, там же (по др. данным — 1591—1661)], французский математик. Был военным инженером. Заложил основы проективной и начертательной геометрии. В своих исследованиях систематически применял перспективное изображение. Первым ввёл в геометрию Бесконечно удалённые элементы.](https://prezentacii.org/upload/cloud/19/08/158199/images/thumbs/screen6.jpg)