Презентация "Аксиомы расположения точек на прямой и плоскости" по математике – проект, доклад
Презентацию на тему "Аксиомы расположения точек на прямой и плоскости" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 15 слайд(ов).
Слайды презентации
Список похожих презентаций
"Разрезание геометрических фигур на части"
ЗАДАЧИ НА РАЗРЕЗАНИЯ. Теорема Бойяи-Гервина гласит: любой многоугольник можно так разрезать на части, что из этих частей удастся сложить квадрат. ..."Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
1. Найти наибольшее значение функции по её графику на [ -5;6] и [-7; 6]. 5 4 -5 у наиб. = 4 [-5; 6] у наиб. = 5 [-7; 6] 1. 2. Найти наименьшее значение ..."Сложение и вычитание рациональных чисел"
I. II. III. IV. Тема: "Сложение и вычитание положительных и отрицательных чисел". Станции: Историческая Биологическая Географическая Математическая. ..."Комбинаторика и вероятность"
Диктант ******- это раздел математики, посвященный задачам выбора и расположения предметов из различных множеств. Произведение натуральных чисел от ...Активные методы обучения на уроках математики и во внеурочной деятельности
Активные методы обучения — это методы, которые побуждают учащихся к активной мыслительной и практической деятельности в процессе овладения учебным ..."Деление на десятичную дробь"
Звонок. Долгожданный дан звонок, Начинается урок Дружно за руки возьмёмся, И друг другу улыбнёмся. Пусть сегодня для нас всех, На уроке сопутствует ...Аксиомы стереометрии и их следствия. Решение задач
Цель урока: обобщение и применение аксиом и их следствий к решению задач. Математический диктант. 1). Сформулируйте аксиомы стереометрии: Аксиома ...Активизация мыслительной деятельности на уроках математики
Активные формы урока. Урок-лекция. Урок-консультация. Урок-практикум Урок-семинар Урок-зачёт. урок-лекция. Зачёт №2 по геометрии в 11 классе 1.Объясните, ...Аксиомы стереометрии Решение задач
Через любые две точки пространства проходит единственная прямая. Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная ...Аксиомы стереометрии и их простейшие следствия
Аксиомы стереометрии. 1)Какова бы ни была плоскость, существуют точки, принадлежащие ей и точки, не принадлежащие ей. 2) Если две плоскости имеют ...Аксиомы стереометрии и их следствия
Цели:. Изучить аксиомы стереометрии: - о взаимном расположении точек, - о взаимном расположении прямых, - о взаимном расположении плоскостей в пространстве. ...Аксиомы стереометрии
1 3 4 5 А1 А3 С1. Дан куб АВСDA1B1C1D1. D1 D С В1 В А M. Точка М лежит на ребре DD1. N. Точка N лежит на ребре CC1. K. Точка K лежит на ребре BB1. ...Аксиомы стереометрии
Аксиомы стереометрии. Сформулируйте содержание аксиом А1, А2, А3, А4 Прокомментируйте их с помощью приведенных ниже рисунков. α С В А. Через любые ...Аксиомы стереометрии
Повторить аксиомы планиметрии Познакомиться с аксиомами стереометрии Уметь соотносить математическую формулировку аксиомы с графическим изображением ...«Задачи на проценты»
Тема урока: Проценты. Тип урока: урок обобщения и систематизации знаний. Цели урока: Образовательные: Обобщение и систематизация знаний учащихся о ...«Действия с дробями», «Нахождение дроби и процентов от числа»
Систематизация знаний по темам: «Действия с дробями», «Нахождение дроби и процентов от числа», Отработка практических навыков выполнения действий ...Активные и Смелые, Артисты и Спортсмены, Аккуратные и Старательные, Артистичные и Симпатичные, Одним словом, наш класс- ПЯТЫЙ АС!
Наш класс весёлый и смешной, Красивый он и смелый. Там есть артисты и певцы, Танцоры и спортсмены. И там улыбка каждый день, И солнце в окна светит, ..."Турнир веселых и смекалистых знатоков истории, физики, химии, математики"
Цели мероприятия: 1.Развитие у учащихся интереса к изучаемым предметам. 2.Показать необходимость знаний по математике в других науках. 3.Формирование ...Аксиомы планиметрии
Аксиома I: Какова бы не была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести ...«Моя математика» - задачи на нахождение целого или части
МАТЕМАТИКА 1 3 4 5 7 6 8 9 0. Работа с числовым рядом. http://www.bajena.com/ru/kids/mathematics/sum-mathematics.php. 1. Прочитайте текст справа и ...Конспекты
Векторы на плоскости
. Конспект. обобщающего урока по теме «Векторы на плоскости». . (геометрия 9 класс). Тема. Систематизация и обобщение изученного материала ...Астрономия на координатной плоскости
Леткова Татьяна Викторовна,. учитель математики. Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа ...Алгебра и начала анализа 10 класс
Алгебра и начала анализа 10 класс(поурочные планы). . 1-е полугодие. . Глава 1. Числовые функции. . Уроки 1-2. Определение числовой функции ...Аксиомы стереометрии
Тема урока. :. Аксиомы стереометрии. Цель урока:. ♦ рассмотреть пространственные аксиомы С1. – С3. и стереометрические аналоги. планиметрических ...Аксиомы стереометрии
. Дмитрикова Ольга Викторовна. учитель математики. МКОУ "Огорская СОШ". с.Огорь. Жиздринский район. Калужская область. класс 10. ...Величины (длина, масса, время, объем) и единицы измерения
Математика. . Тема урока. :. Величины (длина, масса, время, объем) и единицы. . измерения. Цели:. повторить единицы измерения массы, длины, ...Веселая и полезная математика
. Тюрина Валентина Викторовна. 1 квалификационная категория – учитель математики. Город Прокопьевск Кемеровская область. МКОУ «Школа – интернат ...Алгоритм решения задачи на нахождение целого и частей
. Тимошенкова. Ирина Викторовна. Учитель начальных классов. МБ НОУ «Гимназия № 70». Г. Новокузнецк. Алгоритм. решения задачи. ...В гостях у Геометрии. Внутри и снаружи
. Муниципальное бюджетное образовательное учреждение. «Черемшанская средняя общеобразовательная школа № 1». Черемшанского муниципального района ...+ двухзначных и однозначных чисел в пределах 100
УРОК МАТЕМАТИКИ. Тема:. + двухзначных и однозначных чисел в пределах 100 (урок обобщения). Цель:. Создание условий для формирования УУД при ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:6 мая 2018
Категория:Математика
Содержит:15 слайд(ов)
Поделись с друзьями:
Скачать презентацию












![а С 1.Ca; D 2. Da; b 3. b | Cb Db; 4. с | Dc с a = E; c 5. (CD); (DE); (CE)] E ? а С 1.Ca; D 2. Da; b 3. b | Cb Db; 4. с | Dc с a = E; c 5. (CD); (DE); (CE)] E ?](https://prezentacii.org/upload/cloud/18/05/49930/images/thumbs/screen3.jpg)

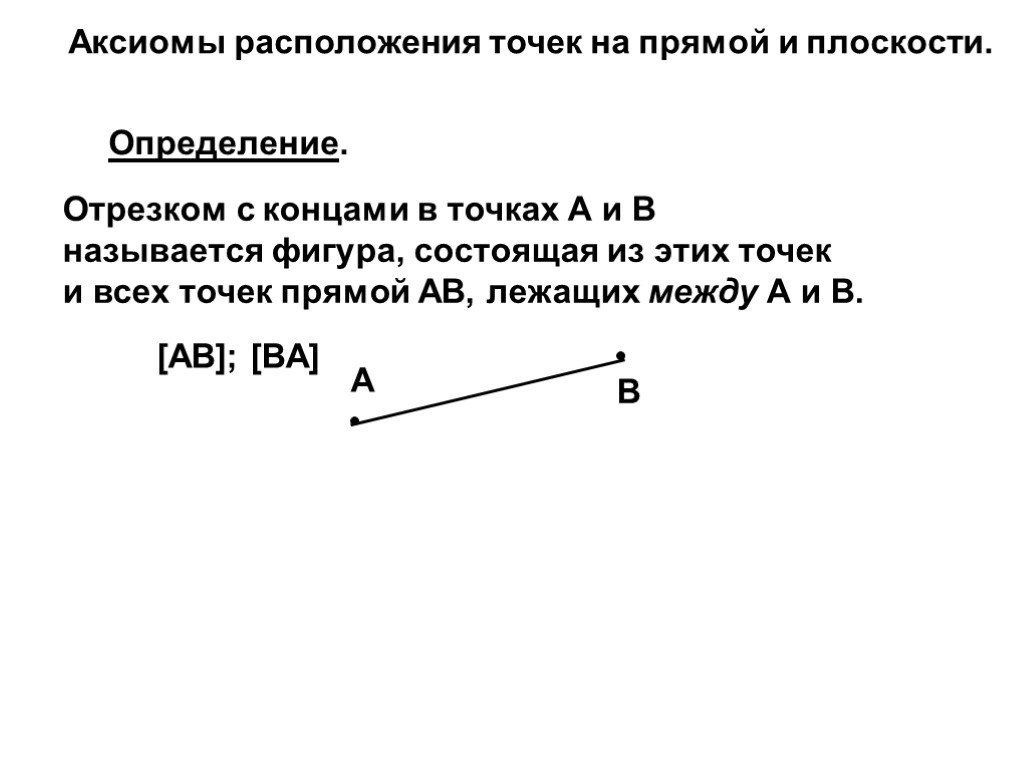
![Отрезком с концами в точках А и В называется фигура, состоящая из этих точек и всех точек прямой АВ, лежащих между А и В. Определение. [AB]; [BA] A B Отрезком с концами в точках А и В называется фигура, состоящая из этих точек и всех точек прямой АВ, лежащих между А и В. Определение. [AB]; [BA] A B](https://prezentacii.org/upload/cloud/18/05/49930/images/thumbs/screen5.jpg)
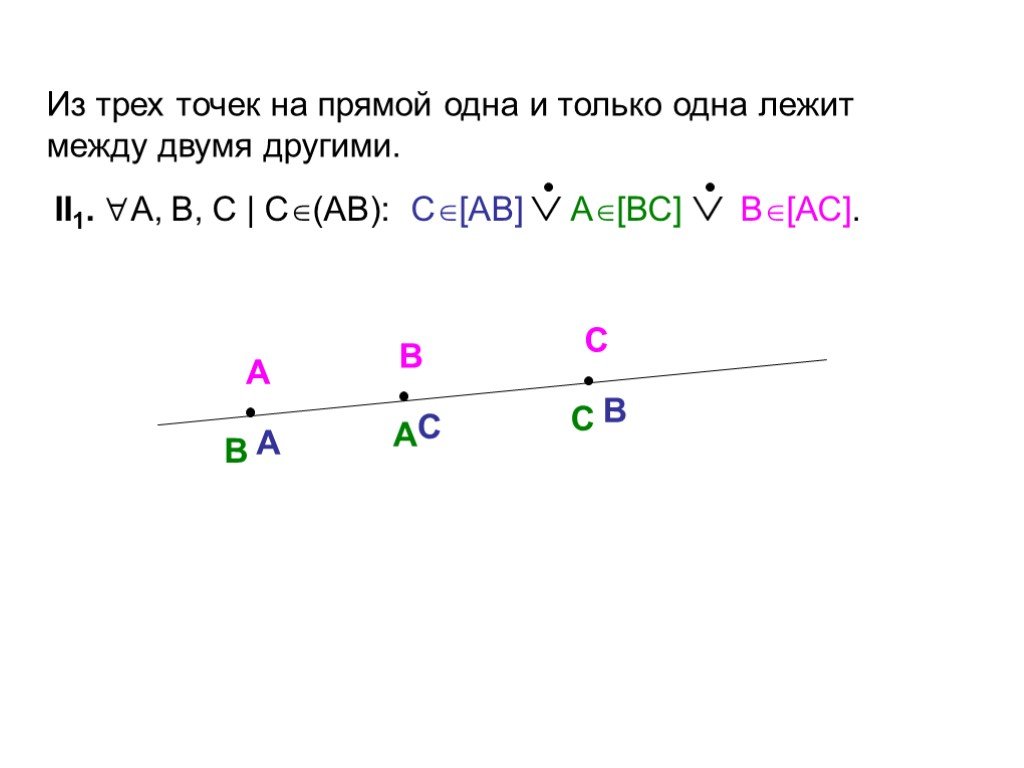
![II1. А, В, С | С(АВ): С[АВ] А[ВС] В[АС]. Из трех точек на прямой одна и только одна лежит между двумя другими. А В II1. А, В, С | С(АВ): С[АВ] А[ВС] В[АС]. Из трех точек на прямой одна и только одна лежит между двумя другими. А В](https://prezentacii.org/upload/cloud/18/05/49930/images/thumbs/screen6.jpg)





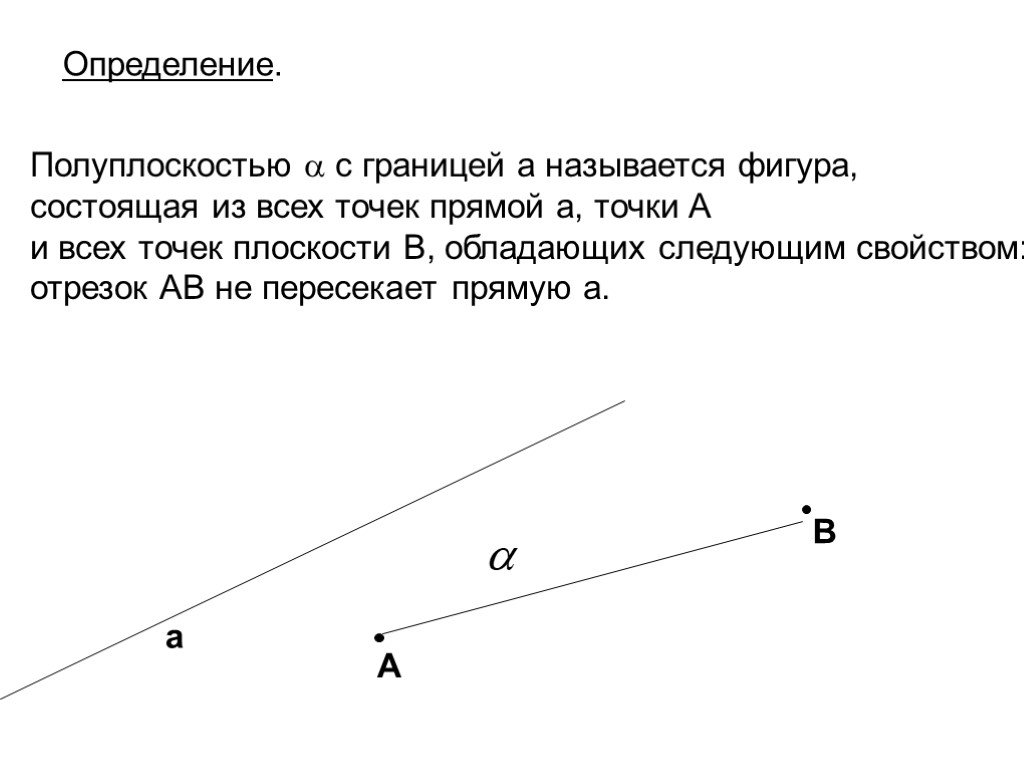
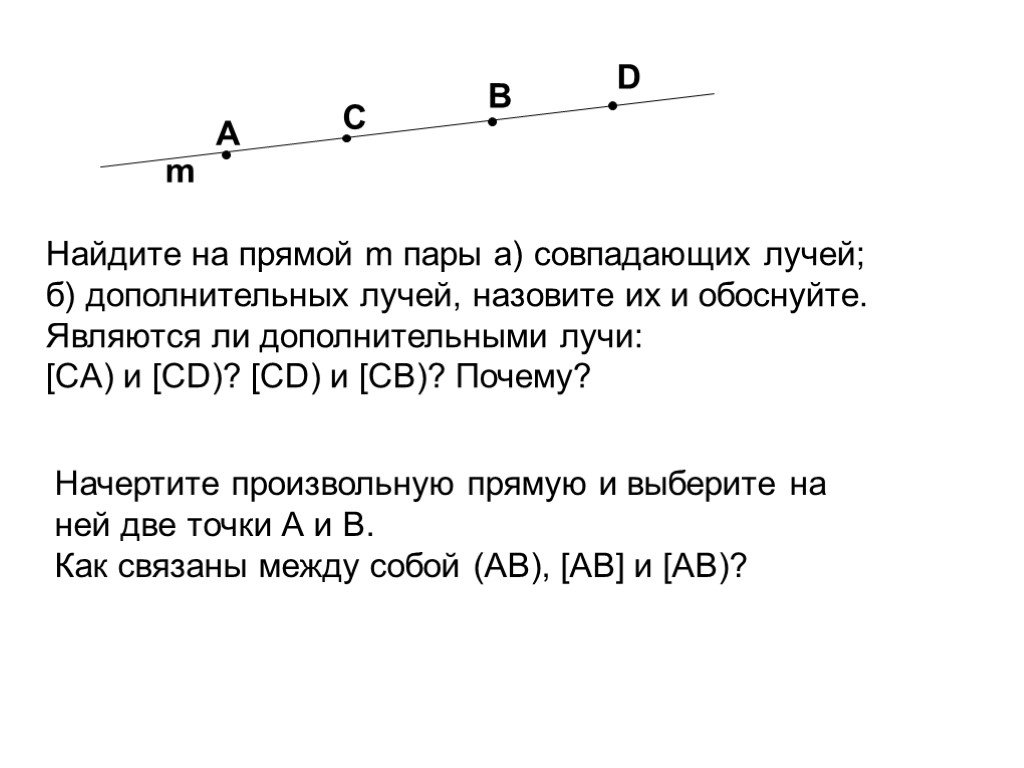
![Найдите на прямой m пары а) совпадающих лучей; б) дополнительных лучей, назовите их и обоснуйте. Являются ли дополнительными лучи: [CA) и [CD)? [CD) и [CB)? Почему? m C. Начертите произвольную прямую и выберите на ней две точки А и В. Как связаны между собой (АВ), [AB] и [AB)? Найдите на прямой m пары а) совпадающих лучей; б) дополнительных лучей, назовите их и обоснуйте. Являются ли дополнительными лучи: [CA) и [CD)? [CD) и [CB)? Почему? m C. Начертите произвольную прямую и выберите на ней две точки А и В. Как связаны между собой (АВ), [AB] и [AB)?](https://prezentacii.org/upload/cloud/18/05/49930/images/thumbs/screen12.jpg)