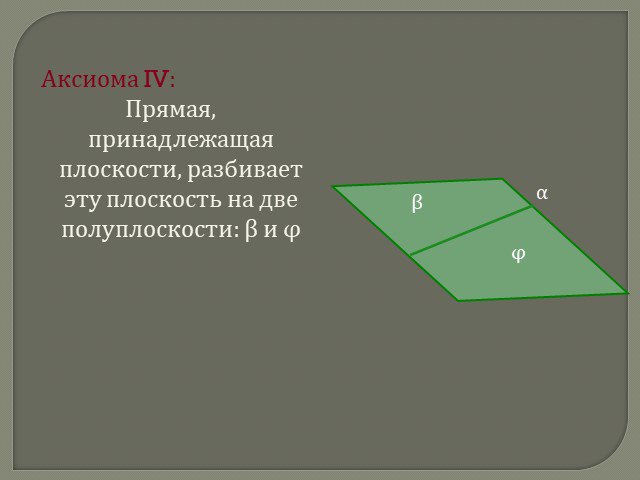
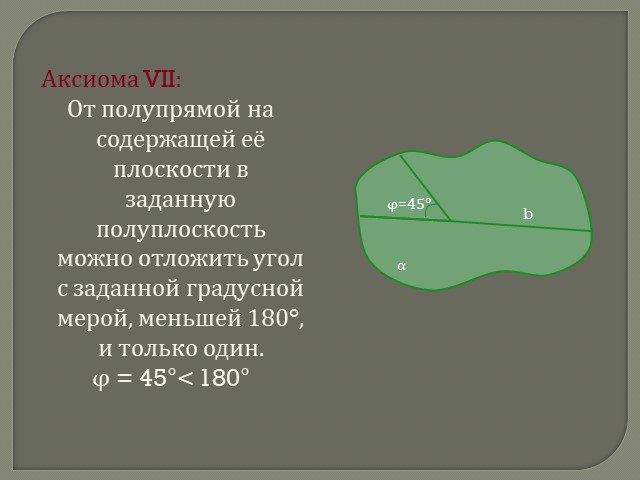
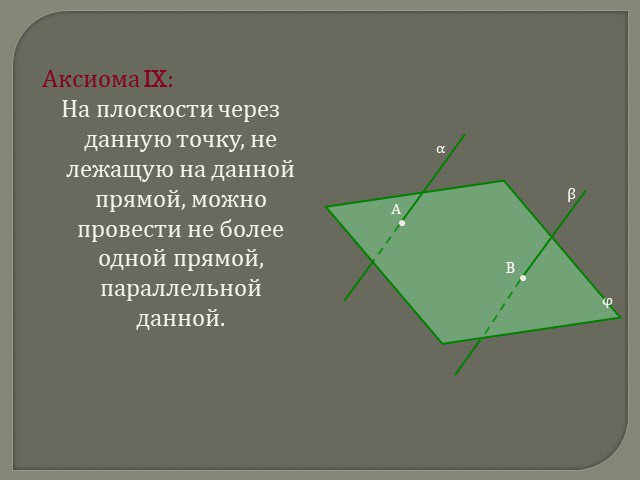
Презентация "Аксиомы планиметрии" по математике – проект, доклад

МАОУ СОШ №17 г.Славянск-на –Кубани Аксиомы планиметрии.

Ковалёва Марина Георгиевна 2011год

Аксиома I: Какова бы не была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну.

А α , В α Э А В А,В=α α

Аксиома II: Из трёх точек на прямой одна и только одна лежит между двумя другими.

С

Аксиома III: Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

АВ > 0

Аксиома IV: Прямая, принадлежащая плоскости, разбивает эту плоскость на две полуплоскости: β и φ

β φ

Аксиома V: Каждый угол имеет определённую градусную меру, большую нуля. Развёрнутый угол равен 180°. Градусная мера угла равна сумме, градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

180

Аксиома VI: На любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один.

АВ α

Аксиома VII: От полупрямой на содержащей её плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один. φ = 45° b φ=45°

Аксиома VIII: Каков бы ни был треугольник, существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.

а А1 В1 С1

Аксиома IX: На плоскости через данную точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.

B

Планиметрия – это раздел геометрии, в котором изучаются фигуры на плоскости. Основными геометрическими фигурами на плоскости являются точка и прямая.

Аксиомы принадлежности

I1 Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. I2 Через любые две точки можно провести прямую, и только одну.

Аксиомы расположения

II1 Из трех точек на прямой одна и только одна лежит между двумя другими. II2 Прямая разбивает плоскость на две полуплоскости.

Аксиомы измерения

III1 Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумму длин частей, на которые он разбивается любой его точкой. III2 Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен равен 180о. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

Аксиомы откладывания

IV1 На любой полупрямой от ее начальной точки можно отложить отрезок, заданной длины, и только один. IV2 От любой полупрямой в заданную полуплоскость можно отложить угол заданной градусной мерой, меньшей 180о, и только один. IV3 Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.

Аксиома параллельности

V Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.