Конспект урока «Декартовы координаты на плоскости» по геометрии
Обобщающий урок по геометрии "Декартовы координаты на плоскости"
Цель урока:
-
истематизировать и обобщить теоретический материал по теме через решение различных задач,
-
проверить знания, умения, навыки учащихся по данной теме;
-
развивать логическое мышление, речь учащихся, интерес к математике;
-
воспитывать чувство взаимного сотрудничества, взаимопомощи, товарищества, любви к родине, сознательное отношение к учебному труду.
Эпиграф
Умение решать задачи - практическое искусство, подобное плаванию или катанию на лыжах, или игре на фортепьяно:
научиться этому можно лишь подражая избранным образцам и постоянно тренируясь...
Д. Пойа.
Содержание и ход урока
I. Вступительное слово учителя. Стихотворение Е. Винокурова "Геометрия". Ребята, сегодня мы проводим урок для того, чтобы систематизировать и обобщить материал по теме через решение различных задач с целью подготовки к контрольной работе.
II. Разминка. Расшифруй высказывание:
Каждый учащийся получает карточку с заданием, решая которую находит нужную букву и пишет ее под номером своей карточки.
1 2 3 4 5 6 7 8
9 10 11 12 13 14
15 16
17 18 19
20 21 22 23
24 25 26 27
28 29
т е р п е н и е г о р ь к о, н о е г о п л о д с л а д о к
| Г | Д | Е | И | К | Л | |
| ( - 4, 3 ) | ( 6,0 ) | 45° | (-1,-1) | -1 ,5 | ( 0, -2) ( 2, 0 ) | ( 0,7 ) ( 7,1) |
| Н | О | П. | Р. | С | Т | Ь |
| ( - 7, 0) | ( - 3, 1) | ( 3,1) | 13 | 150° | ( -1,2) | ( 0,8) |
III. Историческая справка. При решении задач все, наверняка, отметили, что использовали алгебраический аппарат (знания по алгебре). И это не случайно, французский математик Лагранж сказал: "Пока
алгебра и геометрия развивались врозь, их прогресс был медленным, применение - ограниченным; когда же эти две науки были соединены, они стали помогать друг другу и быстро шагать к совершенству".
Первым, кто осуществил взаимопроникновение алгебры и геометрии созданием метода координат был Рене Декарт.
Сообщение о Р.Декарте.
IV. Наряду с декартовой системой координат существуют и другие. Например, полярная система координат. Чтобы построить эту систему, необходимо отметить на плоскости некоторую точку О-полюс (отсюда и название полярная система). Чтобы определить координаты точки, нужно соединить ее с точкой О, определить длину отрезка и величину угла между этим отрезком и полярной осью. Направление полярной оси можно выбрать произвольно. Так географы за направление полярной оси выбирают направление на север, а полярный угол называют азимутом. Артиллеристы же отсчитывают азимут от направления на юг.
V. "Гонка с преследованиями в парах" (для учащихся продвинутого уровня).
Каждой паре учащихся (4 или 5 пар) дается задача, после решения, которой кто-либо из пары готовит решение задачи на доске и дает краткое пояснение к ней.
№ 1. Какими уравнениями задаются линии, ограничивающие фигуру?
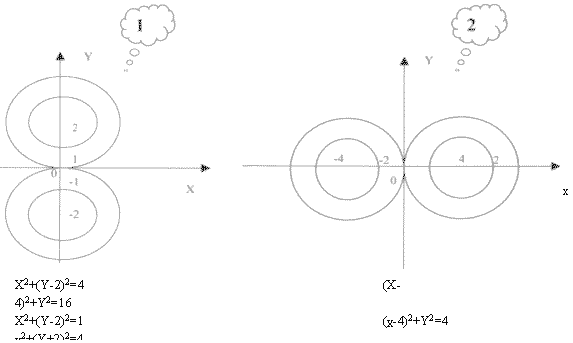
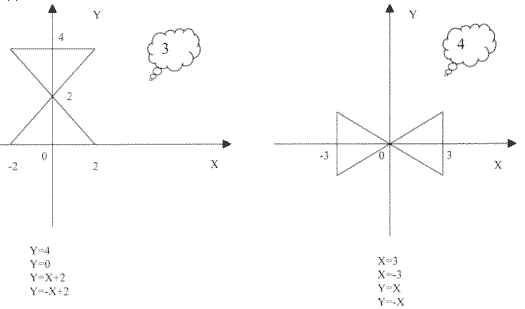
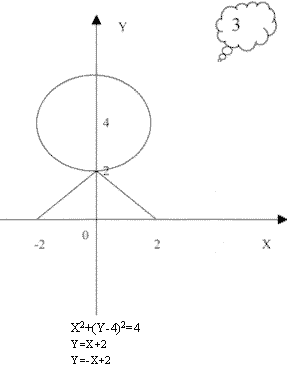
№2. Задачи записаны на доске. 1) Изобрази фигуру, заданную уравнением:
X2+Y2-4Y+2X-20=O.
Пересекается ли она с окружностью (Х-5) 2+(Y-2) 2 =1?
Решение:
(Х2+2Х+1 )+(Y2-4Y+4)-5-20=0.
(X+1)2+(Y-2)2=25
Окружность с центром (-1;2) и R=5.
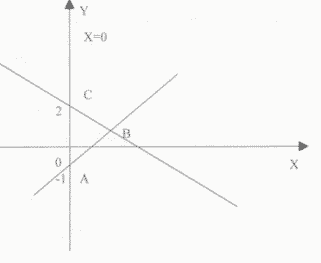
2) Найти координаты вершин треугольника, стороны которого лежат на прямых, заданных уравнениями:
Х=0, X-Y-1=0, X+2Y-4=0 и периметр треугольника.
Y=X-1 (Прямая, пересекающая ось Y в точке (0;-1)).
Y=-0.5X+2 (Прямая, пересекающая ось Y в точке (0;1)). Найдем третью вершину треугольника:
![]()
![]()
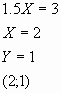
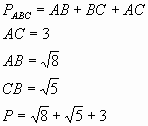
3) Даны точки A(-2;1) B(2;5) C(4;1). Составьте уравнение средней линии треугольника ABC, которая параллельна стороне BC.
Решение: пусть KM - средняя линия треугольника ABC, KM | | BC, значит AK=KB и AM=MC.
Тогда K(0;3) M(1;1).
Y = KX + L
![]()
L = 3
K = -2
Ответ:Y = -2x + 3.
4) Докажите, что треугольник ABC-прямоугольный, если A(1;6) B(-2;3) C(0;1) и найдите его площадь.
Решение:
![]()
![]()
![]()
Т.к. ![]() , т.е.
, т.е. ![]() , то по теореме, обратной теореме Пифагора, треугольник ABC: угол B равен
, то по теореме, обратной теореме Пифагора, треугольник ABC: угол B равен ![]()
S ![]()
![]()
S ![]()
![]()
5) Дана окружность радиуса 5 с центром в начале координат. Некоторая прямая пересекает эту окружность в точках P и Q. Найти координаты точек P и Q, если прямая задана уравнением: X-Y+7=0 и длину хорды PQ.
Решение:
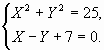
![]()
![]()
![]()
![]()
![]()
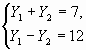
![]()
(-3;4) и (-4;3) - точки пересечения.
![]()
Если найдутся пары, выполнившие задачи задолго до звонка им можно задать вопросы по теории или дать любую из нерешенных задач другими группами.
VI. Остальные учащиеся работают с учителем устно:
1. Какие из данных прямых:
а)параллельны,
б)пересекаются,
в) совпадают ?
2. Какой угол образует прямая 5) с осью абсцисс? В какой точке пересекает ось ординат?
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Назовите координаты центра окружности и её радиус:
а.) ![]()
б.) ![]()
в.) ![]()
3. Задайте прямые и окружность уравнениями.
4. Какие из точек являются серединой отрезка EF,
E(2,1) F(4,5) A(-1,3) C(1,-3) B(-1,-3) D(1,3).
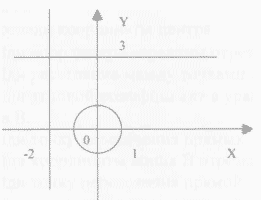
Какие из точек принадлежат прямой X-Y+2=0, окружности X2 + Y2 =10 ?
VII. Решить с учащимися письменно задачу:
1. Составьте уравнение прямой АВ, если А(-3,2) В(5,-2).
2. Составьте уравнение окружности, если АВ-ее диаметр.
Y=КХ+L
![]()
![]()
8K = -4
K=![]()
2=-3(-0.5) + L
L = 0.5
Ответ: ![]()
VIII. Самостоятельная работа по карточкам
Задачи 1,4
IX. Подведение итогов урока.
Что нового узнали. Чем занимались на уроке? Оценки учащимся будут выставлены после проведения самостоятельной работы.
Приложение 1.
О, Петр, ведь ты построил город
Не для умерших - для живых?
Тяжелый дождь бежит за ворот
Окаменевших часовых
Недвижимы аллеи парков,
Прямы проспекты как стрела
Сильней божественных монархов
Здесь геометрия была
Был нежен в башнях цитадели
И кроток лепет голубиц:
И странные на мир глядели
В окно глаза цареубийц.
Гуляют каменные финны,
Курятся трубки из ворот
Вот и построили Афины
Средь топей северных болот!
Налево львы. И львы направо.
А у заставы инвалид
Штык держат вертикально прямо,
Как геометрия велит.
Приложение 2.
Задачи к "Разминке".
Группа А.
1. Определи координаты центра окружности ![]() (-1;2)
(-1;2)
2. Найди координаты середины отрезка CD, если С(-0.5;2) D(-1.5;-4) (-1;1)
3. Найди расстояние между точками А(6;-5) В(1;7) 13
4. Найди угловой коэффициент в уравнении прямой 3X+2Y-10=0. -1.5
Группа В.
5. Найди точку пересечения прямых X+2Y-5=0 и 3X-Y-8=0. (3;1)
6. Найди координаты конца В отрезка АВ, если А(5;-4), С(-1;2)-его середина (_7;0)
7. Найди точку пересечения прямой 4X+3Y-24=0 с осью абсцисс. (6;0)
8. Найди точку пересечения прямой 4X+3Y-24=0 с осью ординат. (0;8)
9. Найди точку пересечения прямых Y=X+4 и Y=-2X-5. (-3;1)
10. Найти координаты точки К, если MN=NK и M(-2;-l) N(-3;l) (-4;3)
Группа С.
11. Найти точку пересечения прямой X-Y-2=0 и окружности![]() (0;-2) (2;0)
(0;-2) (2;0)
12. Найти координаты точек пересечения окружности ![]() с осью ординат. (0;7) (0;1)
с осью ординат. (0;7) (0;1)
13. Найти угол, который образует прямая ![]() с осью абсцисс.
с осью абсцисс. ![]()
14. Найти угол, который образует прямая 2X-3-2Y=0 с осью абсцисс. ![]()
Здесь представлен конспект к уроку на тему «Декартовы координаты на плоскости», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Геометрия Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

