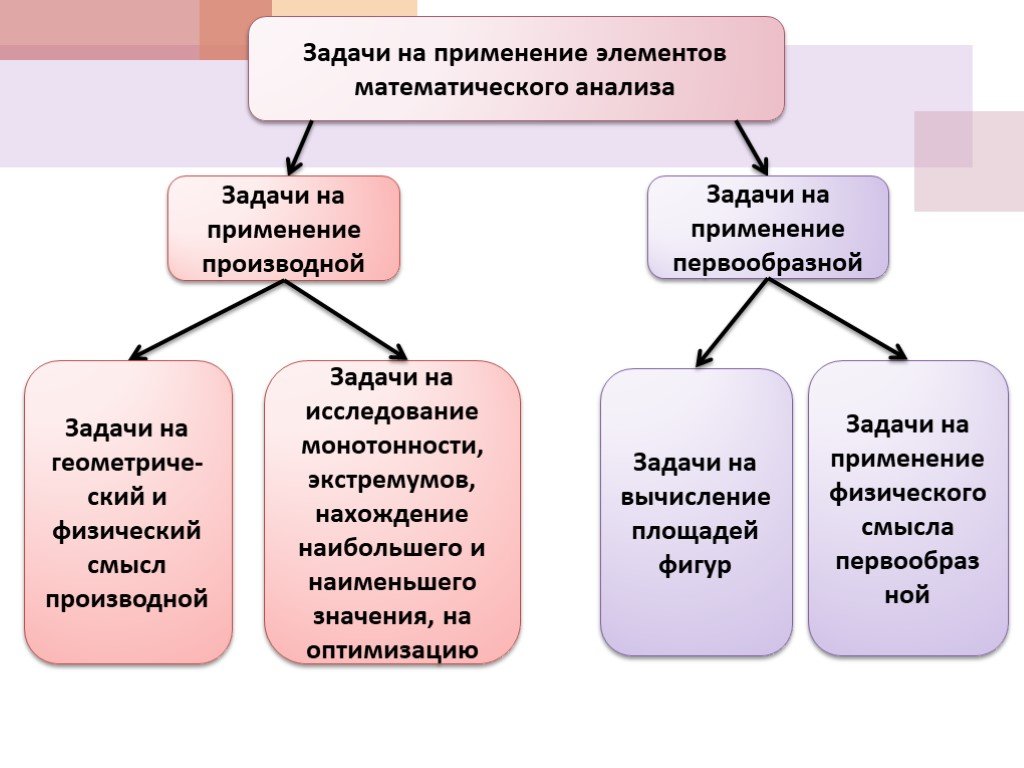
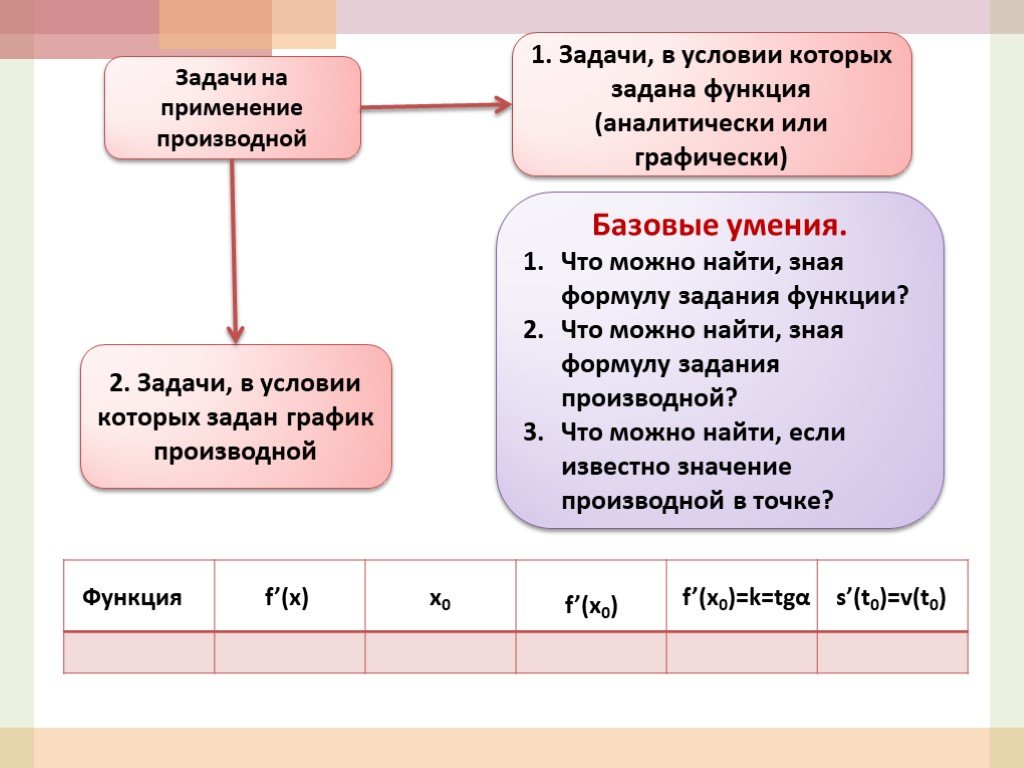
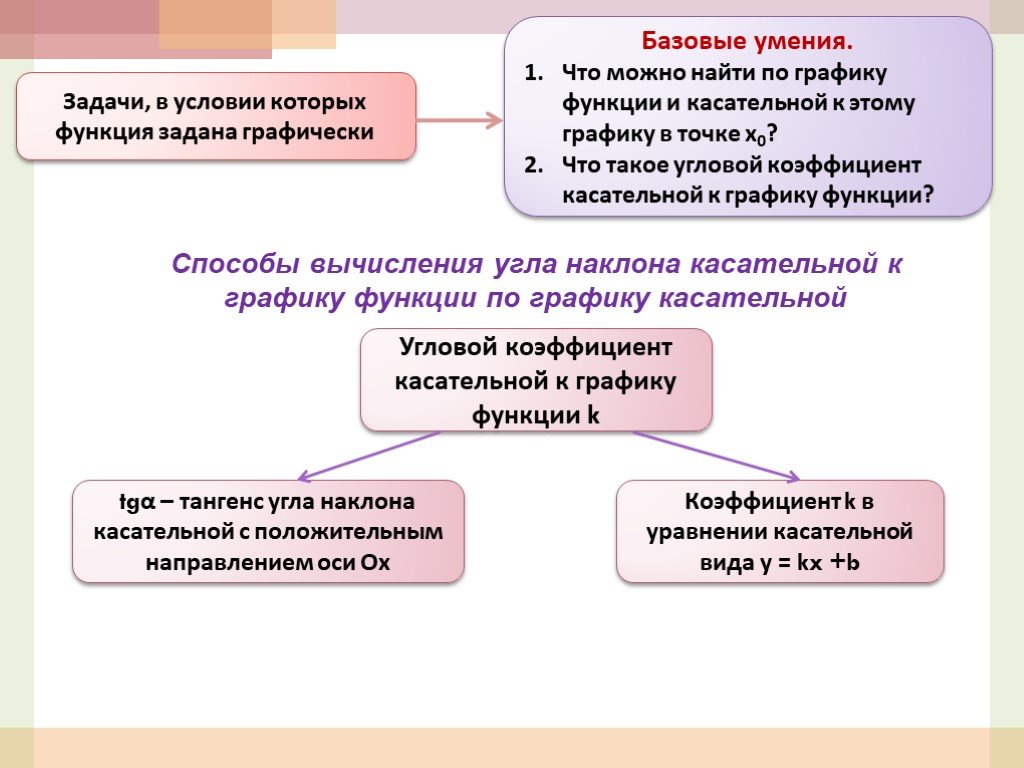
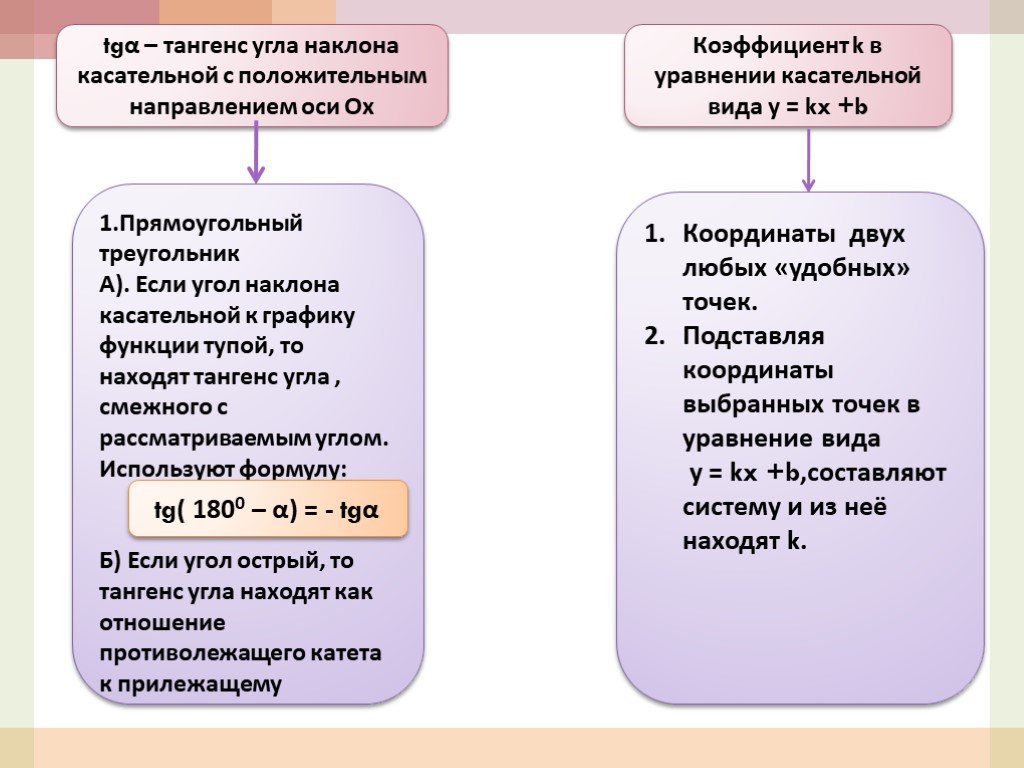
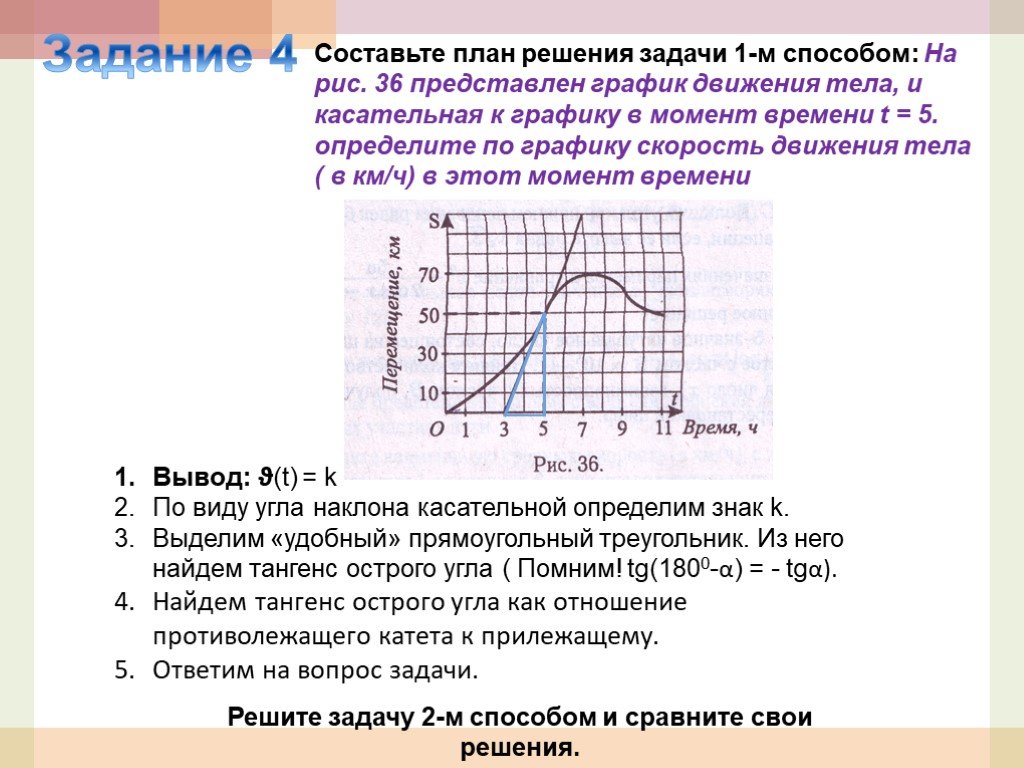
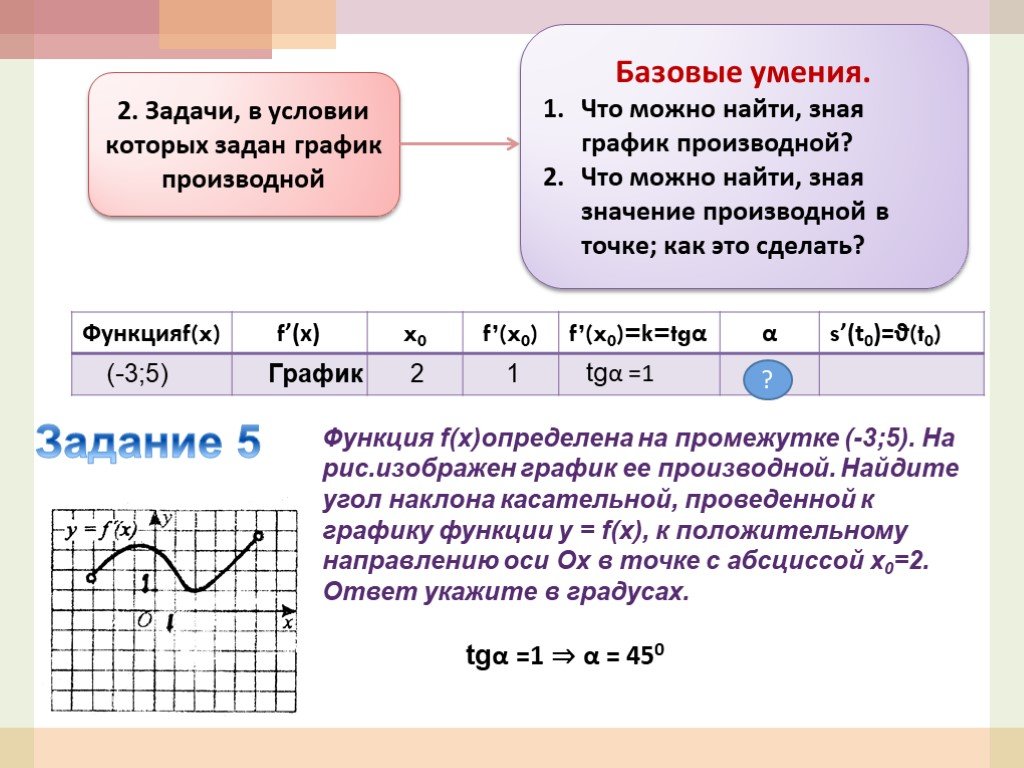
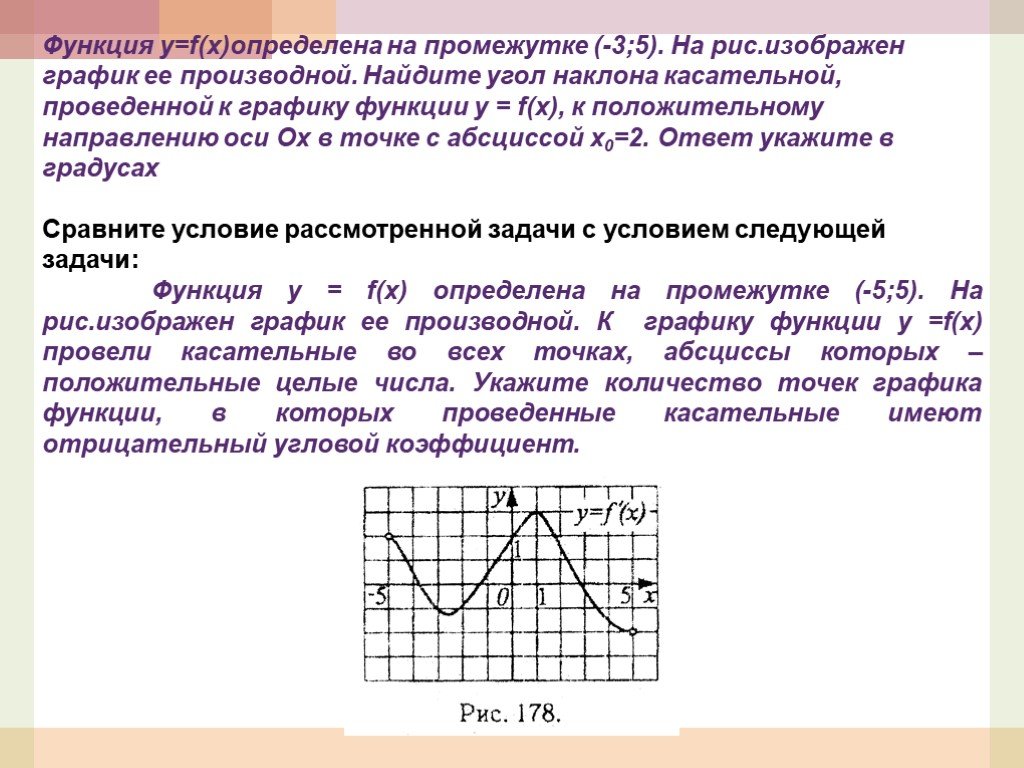
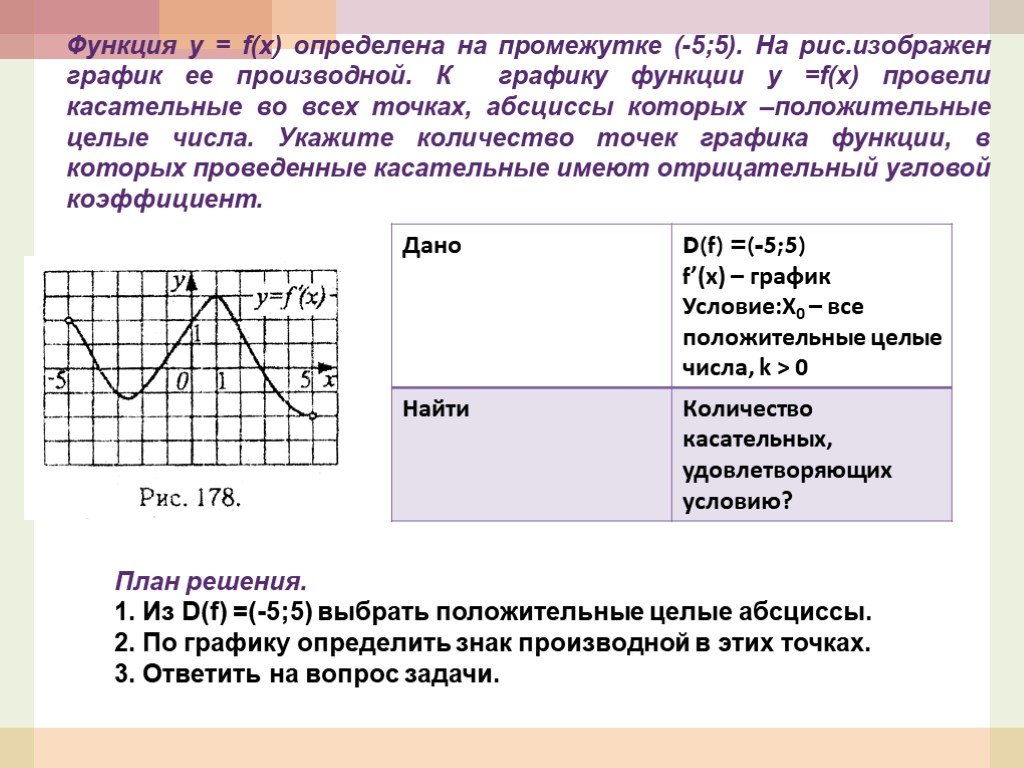
Презентация "Применение элементов математического анализа при решении задач" по математике – проект, доклад
Презентацию на тему "Применение элементов математического анализа при решении задач" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 14 слайд(ов).
Слайды презентации
Список похожих презентаций
Дополнительные построения в трапеции при решении задач
Трапеция – четырёхугольник, две противоположные стороны которого параллельны между собой, а две другие не параллельны. Параллельные стороны трапеции ...Графы и их применение к решению задач
Как известно, умение решать задачи является одним из основных показателей уровня математического развития, глубины освоения учебного материала. Поэтому ...Выбор действий при решении задач
Прочитай вопрос и выбери действие. Приношу свои извинения, но придётся начать заново! - · : +. На сколько 25 больше 5? У Лены 5 игрушек. У Вали в ...Арифметическая и геометрическая прогрессии при решении задач
с и п о г р я е. ПРОГРЕССИЯ. арифметическая аn+1=аn+ d an= a1+d(n-1). геометрическая bn+1= bn * q bn= b1*qn-1. Арифметическая и геометрическая прогрессии ...Графические приемы решения задач с параметрами
Решение уравнений и неравенств, содержащих параметры, является одним из самых трудных разделов элементарной математики. Для их решения обычно требуются ...Алгебра и начала математического анализа
УМК "Алгебра и начала анализа" 10 – 11 класс. Профильный уровень. ЦЕЛЬ: Оказать методическую помощь учителям при выборе УМК для работы в профильных ...Вычитание. Решение задач с помощью действия вычитания
Определение целей урока. Чему должны научиться сегодня на уроке? Какими свойствами вычитания будем пользоваться? Что нужно будет знать, чтобы решить ...Выделение элементов и свойств геометрических фигур
Геометрические фигуры являются эталонами, пользуясь которыми человек определяет форму предметов и их частей. Проблему знакомства детей с геометрическими ...Аксиомы стереометрии и их следствия. Решение задач
Цель урока: обобщение и применение аксиом и их следствий к решению задач. Математический диктант. 1). Сформулируйте аксиомы стереометрии: Аксиома ...Виды занимательных и нестандартных задач
Содержание. Что такое занимательные задачи? Когда появились занимательные задачи? Какие же существуют виды занимательных и нестандартных задач. 1. ...Вечер старинных задач
«…Математику уже затем учить следует, что она ум в порядок приводит» М.В.Лермонтов «Математика – первая из всех наук и полезна, и необходима для них» ...Алгебра высказываний. Решение логических задач
Задача 1: Составьте сложное высказывание в словесной форме из простых, заданных математическим формулировкам:. Высказывание А: «Учащийся Иванов хорошо ...ГИА-2014 (геометрия). Решение задач на углы.
Повторение к ГИА. http://79.174.69.4/os/xmodules/qprint/afrms.php?proj. Углы в треугольниках. № 035C64 Ответ: 8. Центральный угол AOB опирается на ...Дисциплины по выбору из математического блока
Эконометрика. Наука, изучающая количественные и качественные экономические взаимосвязи с помощью математических и статистических методов и моделей. ...Активизация познавательной деятельности при обучении математике
. Народная Классическая Педагогическая Цирковая (эстрадная) Спортивная. Группировка Классификация Систематизация Ассоциация Аналогия Рифмитизация ...Алгоритм решения простых задач
. ЗАДАЧА условие Вопрос, задание. Работа в парах. 1. Налетело 5 гусей-лебедей, подхватили и унесли братца Иванушку. 2. Печка испекла девять ржаных ...Алгоритм решения задач на пропорции
Эпиграф: «Математика обладает двумя великими сокровищами. Первое-это теорема Пифагора, второе-деление отрезка в крайнем и среднем отношении.» Иоганн ...Алгебра и начала анализа 10-11 класс
Числовые функции, заданные формулами y=sin x и y=cos x,называют соответственно - ??? и ???. Числовые функции, заданные формулами y=tg x и y=ctg x, ...Алгебра и начала анализа "Логарифмическая функция"
Содержание. Титульный лист Содержание Определение логарифмической функции Свойства логарифмической функции График логарифмической функции Примеры. ...ГИА-2012. Решение задач по теме "Чтение графиков функций"
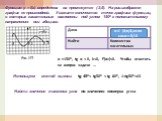
График какой из приведенных ниже функций изображен на рисунке? Задание 17 (№ 197785). Задание 17 (№ 193087). Задание 17 (№ 197695). Задание 17 (№ ...Конспекты
Закрепление вычислительных навыков при решении нестандартных задач
Урок математики в 4-м классе. Тема: ". . Закрепление вычислительных навыков при решении нестандартных задач". . . . Автор: Витязева ...Web -разработка. Применение производной.10 класс
ТЕХНОЛОГИЧЕСКАЯ КАРТА КОНСТРУИРОВАНИЯ УРОКА С ИСПОЛЬЗОВАНИЕ СРЕДСТВ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ. Учитель Беломестнова Наталья Петровна. Предмет, ...Закрепление первоначальных приёмов умножения. Решение обратных задач
Открытый урок по математике во 2 «б» классе,. учитель Заруба Наталья Сергеевна. средняя школа № 96 г. Краснодар. Тема: Закрепление первоначальных ...Закрепление решения примеров и задач в пределах 20
Муниципальное казенное специальное (коррекционное) образовательное учреждение для обучающихся, воспитанников с ограниченными возможностями здоровья ...Геометрический смысл производной. Применение производной к исследованию функций
Урок- консультация по теме «Геометрический смысл производной. Применение производной к исследованию функций». Цель урока. :. содействовать созданию ...Закрепление изученного материала. Решение задач и примеров в пределах 100.
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа № 64 ». города Астрахани. Конспект урока ...Геометрический и физический смысл производной. Применение производной
Учитель математики. КГУ «Экономический лицей». Воробьева. Ирина. Юрьевна. Методическая разработка. урока математики в 10 классе. « Геометрический ...Закрепление решения примеров, простых и составных задач на табличное умножение и деления до 5
Абросимова Марина Владимировна. МБОУ «СОШ№1» г. Топки. . . Учитель начальных классов. Урок математики 3 класс. . Тема. ...Вычитание чисел, полученных при измерении
Конспект урока математики в 7 классе. специальной коррекционной школе. VIII. вида. Автор: Пономарева Елена Анатольевна, учитель. I. категории (математика). ...Закрепление изученного материала. Решение составных задач
ОТКРЫТЫЙ УРОК математики в 3 классе. по традиционной системе, модель «Школа России». Тема урока:. . Закрепление изученного материала. . . ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 мая 2019
Категория:Математика
Содержит:14 слайд(ов)
Поделись с друзьями:
Скачать презентацию