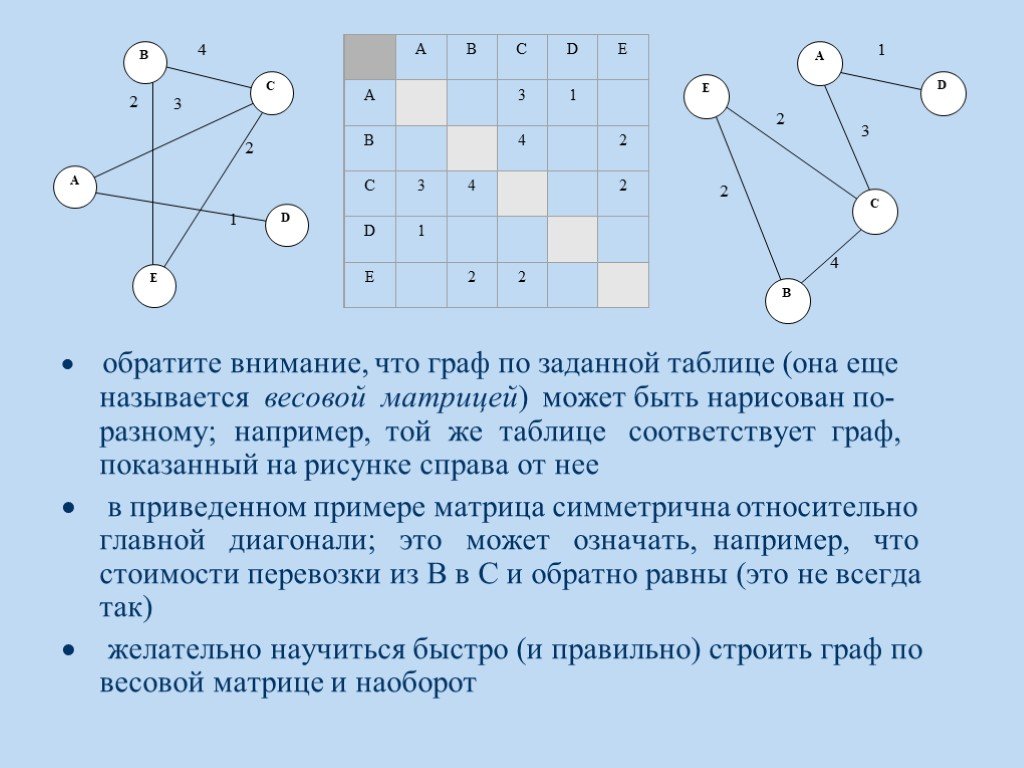
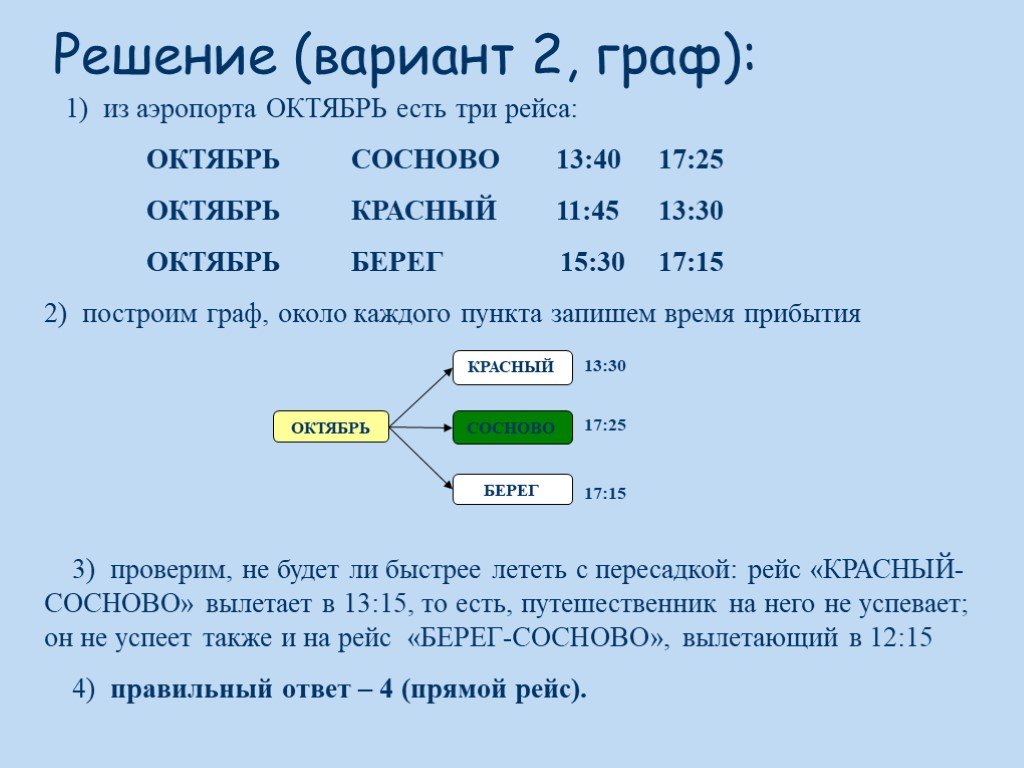
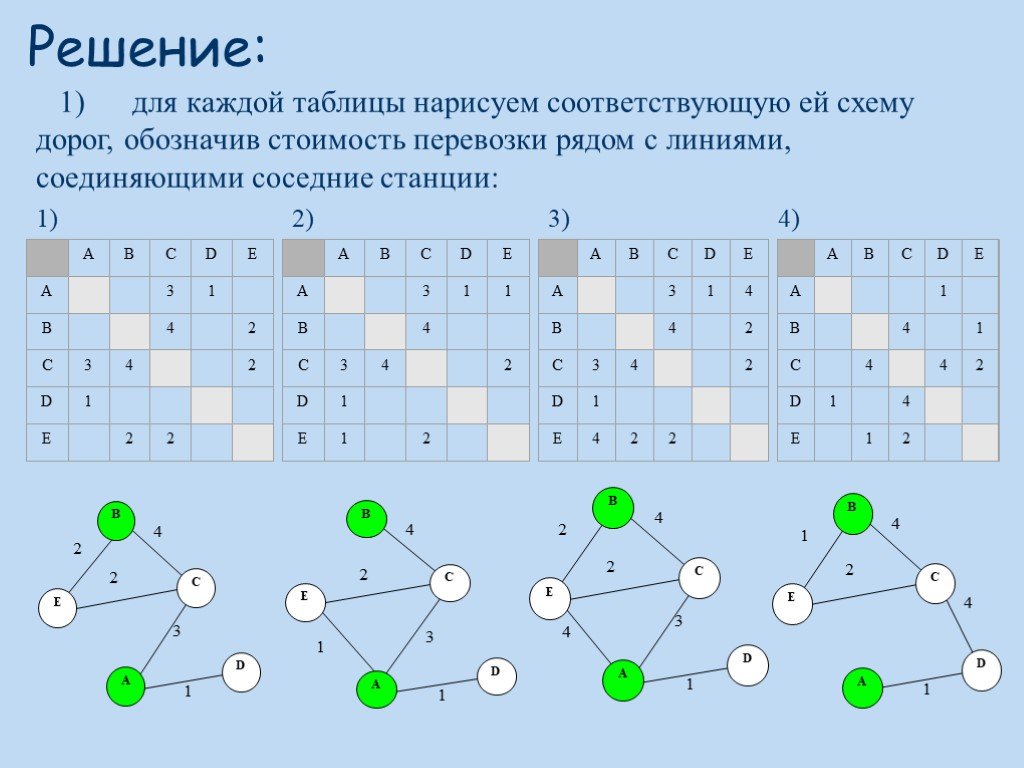
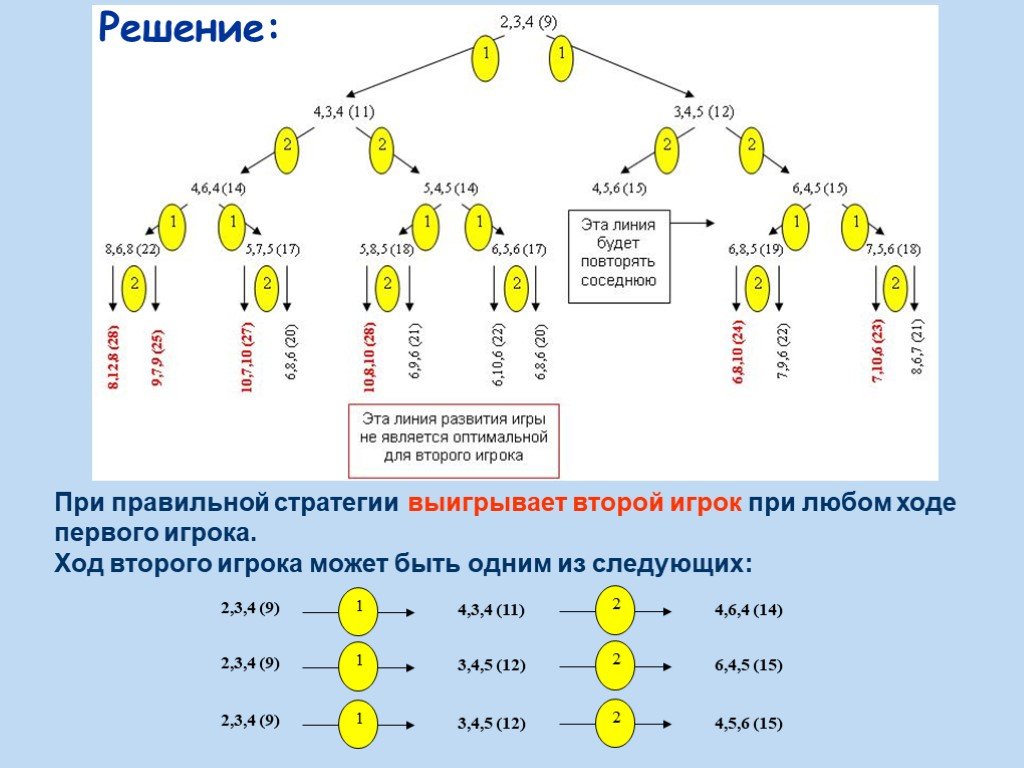
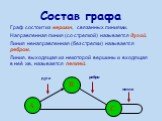
Презентация "Стратегия игры. Решение задач методом «ГРАФЫ»" по математике – проект, доклад
Презентацию на тему "Стратегия игры. Решение задач методом «ГРАФЫ»" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 48 слайд(ов).
Слайды презентации
Список похожих презентаций
Вектор решение задач
Выразить векторы AM, DA, CA, MB, CD через вектор a и вектор b. № 1 Выразить векторы ВС, CD, AC, OC, OA через векторы а и b. Тивякова Л.А. № 2 Выразить ...«Решение задач по математике»
10 февраля. В классе. Задача условие вопрос решение ответ. Быстро и правильно считать. Правильно записывать решение задачи. Кричать и сердиться, когда ...Алггоритм. Решение задач
Задача 1. В урне хранится некоторое количество чёрных и белых шаров. Требуется разложить эти шары по двум корзинам чёрного и белого цвета: белые шары ...Аксиомы стереометрии Решение задач
Через любые две точки пространства проходит единственная прямая. Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная ...Алгебра высказываний. Решение логических задач
Задача 1: Составьте сложное высказывание в словесной форме из простых, заданных математическим формулировкам:. Высказывание А: «Учащийся Иванов хорошо ...Аксиомы стереометрии и их следствия. Решение задач
Цель урока: обобщение и применение аксиом и их следствий к решению задач. Математический диктант. 1). Сформулируйте аксиомы стереометрии: Аксиома ...Бинарный урок геометрии и информатики "Четырехугольники. Решение задач" Лауреат
Проверка домашнего задания. В трапеции АВСD (АD – большее основание) диагональ АС ┴СD и делит ВАD пополам, СDА=60, периметр трапеции – 20 см. Найдите ...ГИА-2014 (геометрия). Решение задач на углы.
Повторение к ГИА. http://79.174.69.4/os/xmodules/qprint/afrms.php?proj. Углы в треугольниках. № 035C64 Ответ: 8. Центральный угол AOB опирается на ...«Решение задач с помощью пропорций»
Найти значение Х: Х:3=4:6 5:Х=2:6 7:3=Х:18 Устная работа. Указать вид пропорциональной зависимости:. Какова зависимость пути от времени? Какова зависимость ...ГИА-2012. Решение задач по теме "Чтение графиков функций"
График какой из приведенных ниже функций изображен на рисунке? Задание 17 (№ 197785). Задание 17 (№ 193087). Задание 17 (№ 197695). Задание 17 (№ ...ГИА-2012. Решение планиметрических задач на нахождение углов геометрических фигур
1 3 4 5 6 7 8 9 10 11. Вашему вниманию представлено двенадцать прототипов задачи № 11 Открытого банка заданий по математике. ГИА – 2012. Два острых ...Вычитание. Решение задач с помощью действия вычитания
Определение целей урока. Чему должны научиться сегодня на уроке? Какими свойствами вычитания будем пользоваться? Что нужно будет знать, чтобы решить ...Выбор действий при решении задач
Прочитай вопрос и выбери действие. Приношу свои извинения, но придётся начать заново! - · : +. На сколько 25 больше 5? У Лены 5 игрушек. У Вали в ...Виды занимательных и нестандартных задач
Содержание. Что такое занимательные задачи? Когда появились занимательные задачи? Какие же существуют виды занимательных и нестандартных задач. 1. ...8 класс "Решение квадратных уравнений"
. . . . . . «Уравнение – это золотой ключ, открывающий все математические тайны». . Цель: привести в систему знания о квадратных уравнениях и умение ...Длина окружности. Площадь круга. Коллекция задач для 6 класса
. Великий древнегреческий математик Архимед (III в. до н.э.), выполнив множество измерений, установил, что длина окружности примерно в раза больше ...Графические приемы решения задач с параметрами
Решение уравнений и неравенств, содержащих параметры, является одним из самых трудных разделов элементарной математики. Для их решения обычно требуются ...Арксинус. Решение уравнения sin t = a
Цели. Изучить определение арксинуса числа. Изучить формулы решения простейшего тригонометрического уравнения sin t = a. Повторим. Что называется синусом ...Арифметическая и геометрическая прогрессии при решении задач
с и п о г р я е. ПРОГРЕССИЯ. арифметическая аn+1=аn+ d an= a1+d(n-1). геометрическая bn+1= bn * q bn= b1*qn-1. Арифметическая и геометрическая прогрессии ...Конспекты
Деление с остатком. Решение задач на деление с остатком
. Урок математики. . «Деление с остатком. Решение задач на деление с остатком». . Учитель:. Московченко Е. Н. ...Деление и умножение на однозначное число. Решение задач с использованием экологических понятий и терминов
Полякова Елена Александровна. учитель начальных классов. НОУ «Школа – интернат №8 ОАО «РЖД». УРОК . МАТЕМАТИКИ. (3. класс). Тема. : «. ...Деление с остатком. Решение задач
Урок математики в 3 классе по теме. «Деление с остатком. Решение задач». . Учитель начальных классов. МОУ «СОШ № 8» г.Саранск. Клёмина Татьяна ...Деление двузначного числа на однозначное и двузначное число, деление чисел с остатком, решение задач
. ТЕМА: «. Деление двузначного числа на однозначное и двузначное число, деление чисел с остатком, решение задач». . Сухова Т.А. . ...Деление двузначного числа на однозначное. Решение арифметических задач
. УРОК 15 (задания 87-93). . . Учебный предмет:. математика. Класс:. 3. . Авторы учебника:. . Истомина Н.Б., Редько З.Б., Иванова И.Ю. УМК ...Действия с составными именованными числами. Решение задач различного вида
Урок математики в 4 классе. . По программе «Школа 2100». Тема урока:. “Действия с составными именованными числами. Решение задач различного вида. ...Действия с величинами. Соотношение цены, количества, стоимости. Решение задач, выражений
Автор: Енина Н.В. учитель начальных классов МКОУ НОШ №17 ст.Зольской,. . Ставропольский край. . Урок математики в 3-м классе. УМК «Гармония». ...Геометрическое решение негеометрических задач
Урок по теме:. «Геометрическое решение негеометрических задач». Сивак Светлана Олеговна. учитель математики. высшей категории. Гимназии №56. ...Диаграммы. Решение задач
Автор (фамилия, имя, отчество полностью) загружаемого материла. . . Гиль Наталья Николаевна. . . Место работы (полное наименование ОУ, город, ...Закрепление пройденного. Решение текстовых задач
. Рыжикова Любовь Петровна. МБОУ Ямновская ООШ. с.Ямново, Борского р-на. учитель начальных классов. Тема урока:. Урок «Закрепление пройденного. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:1 января 2019
Категория:Математика
Содержит:48 слайд(ов)
Поделись с друзьями:
Скачать презентацию