Презентация "Производная" (10 класс) по математике – проект, доклад
Презентацию на тему "Производная" (10 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 12 слайд(ов).
Слайды презентации
Список похожих презентаций
Производная функции
Проблемный вопрос. Можно ли находить производные, не используя определение? Существуют ли более удобные способы? Цели и задачи. Научиться находить ...Производная функции
Определение производной. Пусть функция y = f(x) определена в некотором интервале (a; b). Аргументу x придадим некоторое приращение :. х f(x ) x+Δx ...Производная сложной функции
Производная сложной функции. Сложная функция. Производная простой функции. Простая функция. Пример:. . . . ...Производная Изучение нового материала по теме
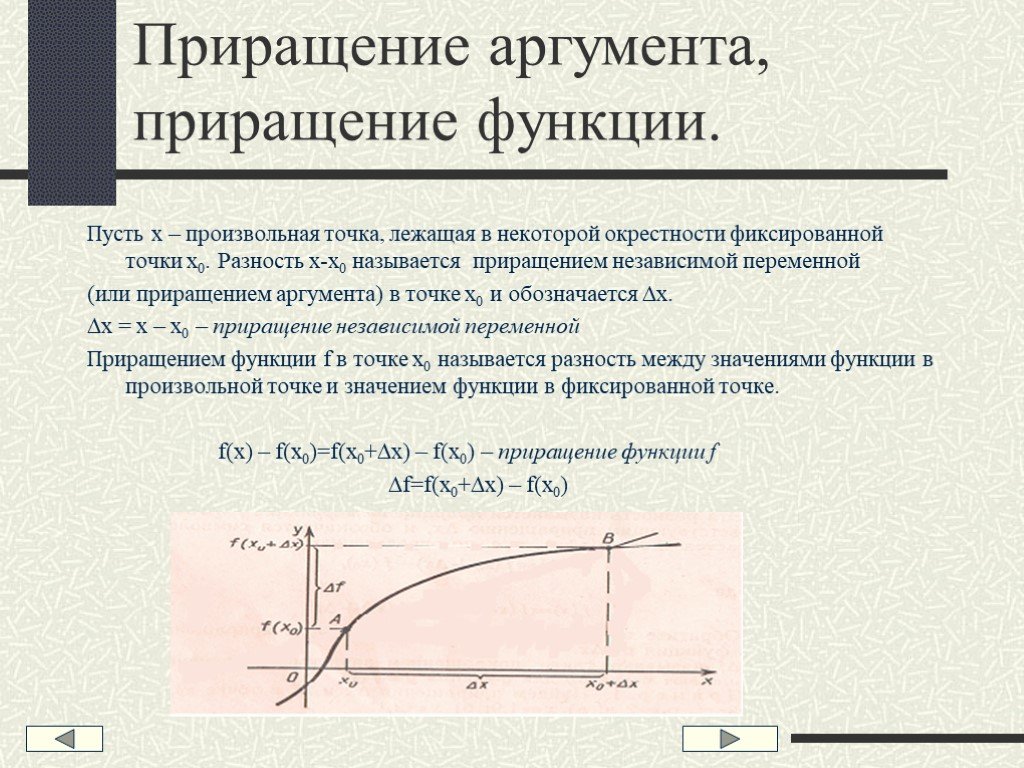
x0 x f(x0) x f(x) f y=f(x) x = x - x0 x = x0 + x. приращение аргумента. f = f(x) – f(x0) f(x) = f(x0) + f. приращение функции. f f(x0 + x) ...Производная показательной функции
www.thmemgallery.com Company Logo План урока. Устная работа. Определение производной. Правила дифференцирования. Производные элементарных функций. ...Производная и её применение
Под темы:. Производная Применение производной к приближенным вычислениям в геометрии и физике Применения производной к исследованию функций. Найдите ...Производная функции. Геометрический смысл производной
Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная. Производная. — это скорость ...Производная и ее применение
«Если продолжить одно из маленьких звеньев ломаной, составляющей кривую линию, то эта продолженная таким образом сторона будет называться касательной ...Производная и ее применение
Укажите тангенс угла наклона касательной к графику функции в точке с абсциссой х0. Укажите угловой коэффициент касательной к графику функции в точке ...Производная и графики функций
Доказать, что функция монотонна на заданном промежутке:. Дана непрерывная на функция. Используя график производной этой функции, определите, имеет ...Производная
Цели и задачи:. закрепление и обобщение знаний по данной теме повторение определения производной, правила нахождения производной; закрепление умения ...Производная
Содержание. Таблица производных Применение производной. Производная в физике Геометрический смысл производной Уравнение касательной к графику Возрастание ...Производная и её применение
Цель работы:. Закрепление изученного материала по теме «Производная» и ознакомление с её прикладной частью. План работы:. 1.Исследование функции на ...Производная функции в точке
Вопросы теории. 1. Что называется производной функции f(x) в точке х? 2. В чем состоит геометрический смысл производной? 3.Сформулировать правила ...Производная функции
Задание № 1. 1. На рисунке изображен график функции y=f(x) и касательная к нему в точке с абсциссой х0 Найдите значение производной в точке х0 1) ...Производная
ТЕМА ПРОЕКТА: ПРОИЗВОДНАЯ. Из истории; Понятие о производной; Правила вычисления производной: -Основные правила дифференцирования, -Производная степенной ...Синус, косинус, тангенс и котангенс, алгебра,
Синус и косинус. Что будем изучать:. Определение синуса и косинуса. Определение тангенса и котангенса. Основное тригонометрическое тождество. Примеры ...Тригонометрические функции углового аргумента - алгебра,
Тригонометрическая функция углового аргумента. Что будем изучать:. Определение. Примеры. Вспомним геометрию. Градусная мера угла. Радианная мера угла. ...Конспекты
Производная показательной функции
Конспект урока по теме «Производная показательной функции» в 11 классе. Цель:. Ввести понятие «экспоненты», «натурального логарифма», сформировать ...Производная и первообразная
Урок – соревнование: Производная и первообразная. Клименко Ольга Андреевна, учитель математики 2 категории. . Цель урока. : повторение ранее изученного ...Производная показательной и логарифмической функции
КГУ «Средняя школа №7 города Зыряновска». «Производная показательной и логарифмической функции». Учитель: ...Производная и ее применение
Автор: Файзуллина Гульнара Мухаметовна. МОБУ СОШ с.Курятмасово. Тема урока :. Производная и ее применение. Класс 11. Цели урока. :. знать ...Производная и ее применение
Урок 1. Повторение:. производная и ее применение. . Цели урока. :. знать определение производной, правила нахождения производной; уметь находить ...Производная сложной функции
Открытый урок. . по теме: «Производная сложной функции». . . Тип урока:. комбинированный. Цели:. образовательная:. - формирование умения ...Производная
Тема урока-консультации:. «Производная». Класс:. 11. Тип урока:. обобщение и закрепление изученного материала. Цели урока:. 1) в направлении ...Производная и ее геометрический смысл
Урок разноуровневого обобщающего. . повторения в 11 классе на тему. . «Производная и ее геометрический смысл». Урок подготовила и провела:. ...Производная и ее геометрический смысл
Открытый урок обобщения и систематизации знаний по теме «Производная и ее геометрический смысл». Цели урока:. . . ¨. дидактическая. – формирование ...Производная в задачах ЕГЭ. Задача В9
МОУ "Гимназия "Дмитров"". Московская область. г. Дмитров. Конспект урока по математике в 11 классе. "Производная в задачах ЕГЭ. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:7 сентября 2018
Категория:Математика
Классы:
Содержит:12 слайд(ов)
Поделись с друзьями:
Скачать презентацию