Презентация "Треугольники" по математике – проект, доклад
Презентацию на тему "Треугольники" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 30 слайд(ов).
Слайды презентации
Список похожих презентаций
Треугольники
Рекомендации для проведения игры. Игра заимствована из телевикторины «Что? Где? Когда?», поэтому при проведении её целесообразно придерживаться ритуала, ...Треугольники в природе
Бермудский треугольник — район в Атлантическом океане, в котором якобы происходят таинственные исчезновения морских и воздушных судов. Район ограничен ...Треугольники
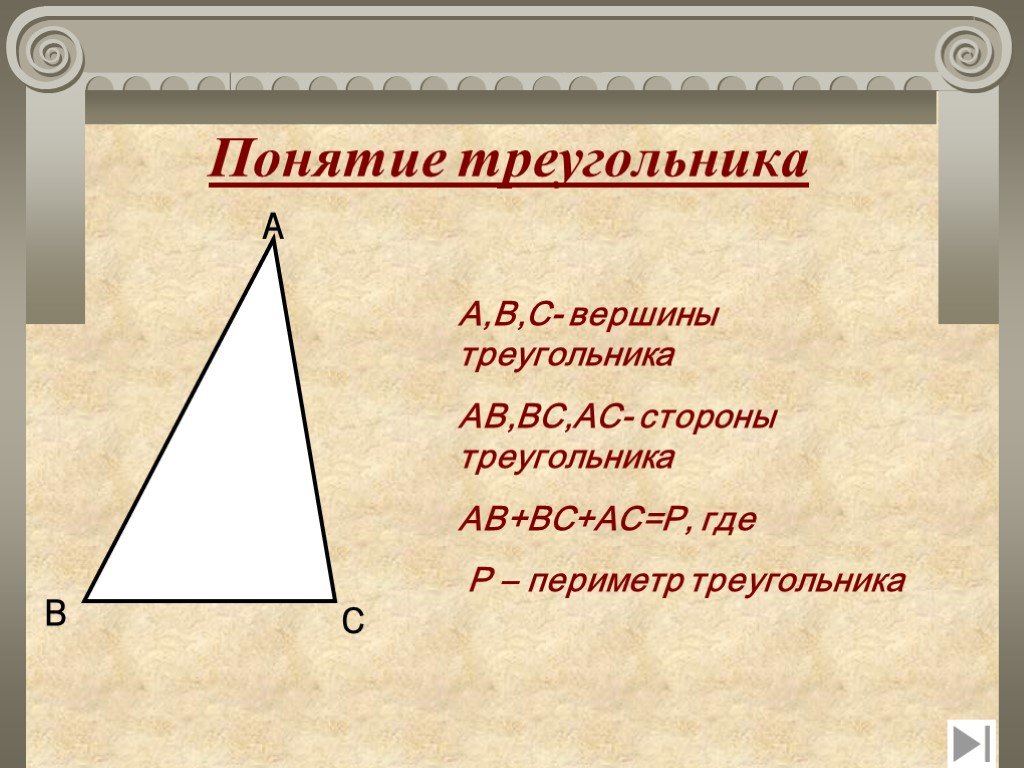
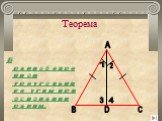
Закончи предложение. 1. Треугольником называется геометрическая фигура, состоящая из трех точек……… 2. Точки А, В, С ∆АВС называются………………. этого треугольника. ...Треугольники
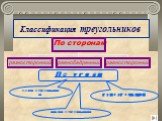
Разносторонний (a) Равнобедренный (b) Равносторонний (c) Прямоугольный (d) Подобные треугольники (e). a) b) c) d) e). Виды треугольников. «…Здесь ...Треугольники
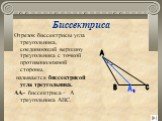
1) Отметим какие-нибудь три точки, не лежащие на одной прямой; 2) Соединим их отрезками. А В С. Точки А, В и С называются вершинами треугольника; ...Треугольники
Задача 1. Найдите высоту прямоугольного треугольника, проведенную к гипотенузе, если биссектриса острого угла делит катет на отрезки, равные 2 и 4. ...Треугольники
Треугольники 5 класс. Содержание Треугольник Периметр треугольника Виды треугольников: - по величине наибольшего угла - по длине стороны Равнобедренный ...Треугольники вокруг нас
ТРЕУГОЛЬНИКИ В АРХИТЕКТУРЕ. 13-метровая скульптура невозможного треугольника из алюминия была воздвигнута в 1999г. в городе Петр (Австралия) . Треугольник ...Треугольники и их виды
«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Всё вокруг – геометрия» Ле Корбюзье. Первичная актуализация. ...Решение задач - Треугольники
8 9 10 11 14 15 16 17 18 1 3 4 5 6 13 19 7. Второй признак равенства треугольников. Третий признак равенства треугольников. Решение задач на применение ...Треугольники
Закончи предложение. 1. Треугольником называется геометрическая фигура, состоящая из трех точек……… 2. Точки А, В, С ∆АВС называются………………. этого треугольника. ...Начертательная геометрия
Оглавление. 1.1 ТОЧКА Проецирование точки на плоскости проекций Точка на комплексном чертеже 1.2 ПРЯМАЯ Следы прямой Определение истинной величины ...Наглядная геометрия для начальной школы
Содержание. Урок 1 Урок 2 Урок 3 Урок 4. Урок 1 Путешествие в страну Геометрия. Знакомство с веселой Точкой. Начнем урок. Наша школьная страна. Не ...Наглядная геометрия
геометрия Урок 1. Сегодня мы отправляемся в путешествие в удивительную страну, которая называется ГЕОМЕТРИЯ. Что такое геометрия? Какими инструментами ...Математика геометрия
ГЛАВА 1. История математики. ГЛАВА 2. Математика. ГЛАВА 3. Геометрия И последнее…. Что такое математика. Она изучает числа и величины, отношения и ...Что изучает геометрия
Что изучает геометрия. Откуда пошла геометрия. География Геология Геодезия Геоботаника Геоакустика. Геология – наука о составе, строении и истории ...Страна геометрия
Правительство. Отдел планирования. Отдел проектирования. Район археологических раскопок. Юбилей Первые поселения. Силурийский период. Средневековье ...Простая геометрия в архитектуре различных эпох и культур
Архитектура. Уже в XII в. архитектура понимается уже как наука, как знание, как геометрия, имеющая практическое приложение, как деятельность, требующая ...Поворот и геометрия
ВСПОМИНАЕМ. Что называют параллельным переносом на заданный вектор? На что при параллельном переносе отображается прямая? Является ли параллельный ...Неевклидова геометрия
Мы выбрали эту тему так как она нас очень заинтересовала тем , что геометрия Лобачевского очень полезна в современном мире, и мы хотим немного рассказать ...Конспекты
Треугольники - вокруг нас
Муниципальное образовательное учреждение. «средняя общеобразовательная школа №29». города братска иркутской области. . . Треугольники ...Треугольники и их виды
Тема урока «Треугольники и их виды». Цели. : научить выделять признаки различных видов треугольников, объединять треугольники по группам на основе ...Треугольники
Математика. Модуль геометрия. Тема урока. Треугольники. Тип урока. . Урок обобщения и закрепления знаний. Вид урока. . Практическая работа. ...Треугольники
Урок обобщающего повторения. . по геометрии в 9-м классе на тему: "Треугольники". . Тип урока:. урок обобщения и систематизации знаний. ...Треугольники
Тема урока «Треугольники». Цели урока:. Образовательные: формирование умений применять признаки равенства треугольников для решения задач, распознавать ...Треугольники
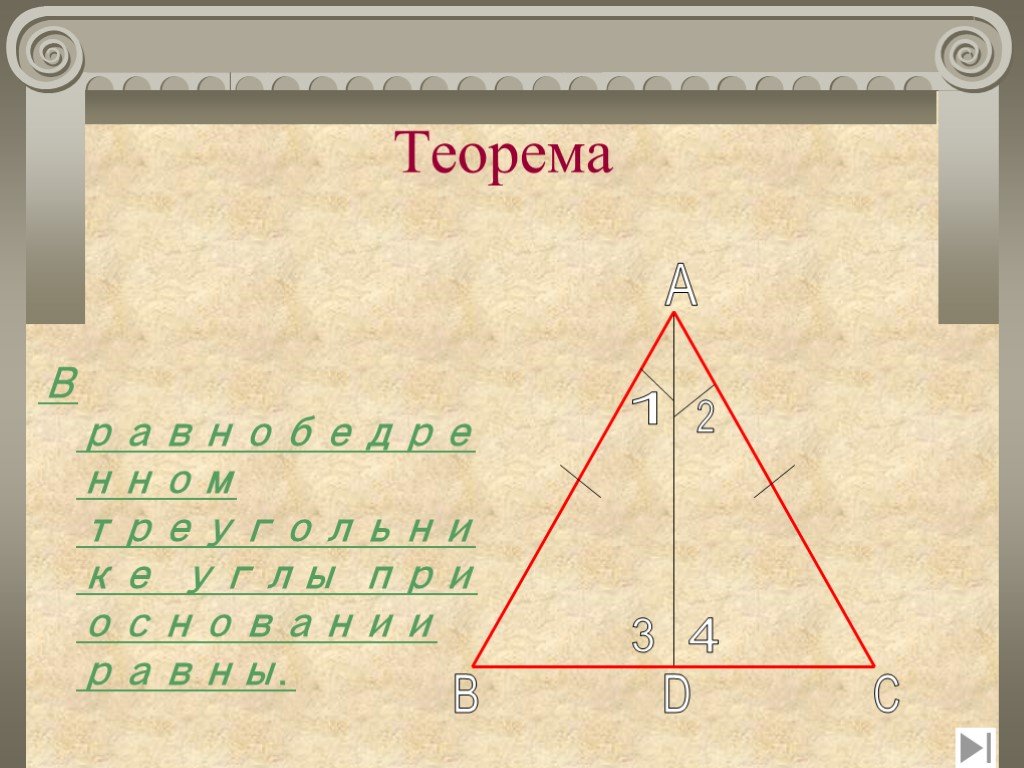
Конспект урока геометрии для 7 класса «Треугольники». Сумма углов любого треугольника равна 180°. . В равнобедренном треугольнике углы при ...Треугольники
Технологическая карта урока. . Класс:. 9. Предмет. : математика. Теме урока. : Решение задач по теме «Треугольники». Дидактическая цель ...Треугольники
МБОУ «Кипринская ООШ» учитель математики Кашичкина Лариса Николаевна. . Конспект урока. «Треугольники». Цели урока:. . Повторение и систематизация ...Треугольники
Треугольники. . ( Геометрия, 7 класс). Автор:. Шапеева Анфиса Васильевна,. . учитель математики. . МАОУ «Гимназия ...Треугольники
Муниципальное бюджетное общеобразовательное учреждение. г. Абакана. «Средняя общеобразовательная школа № 18». Конспект урока по математике ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:30 января 2019
Категория:Математика
Содержит:30 слайд(ов)
Поделись с друзьями:
Скачать презентацию