Презентация "Исследование функции" по математике – проект, доклад
Презентацию на тему "Исследование функции" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 18 слайд(ов).
Слайды презентации
Список похожих презентаций
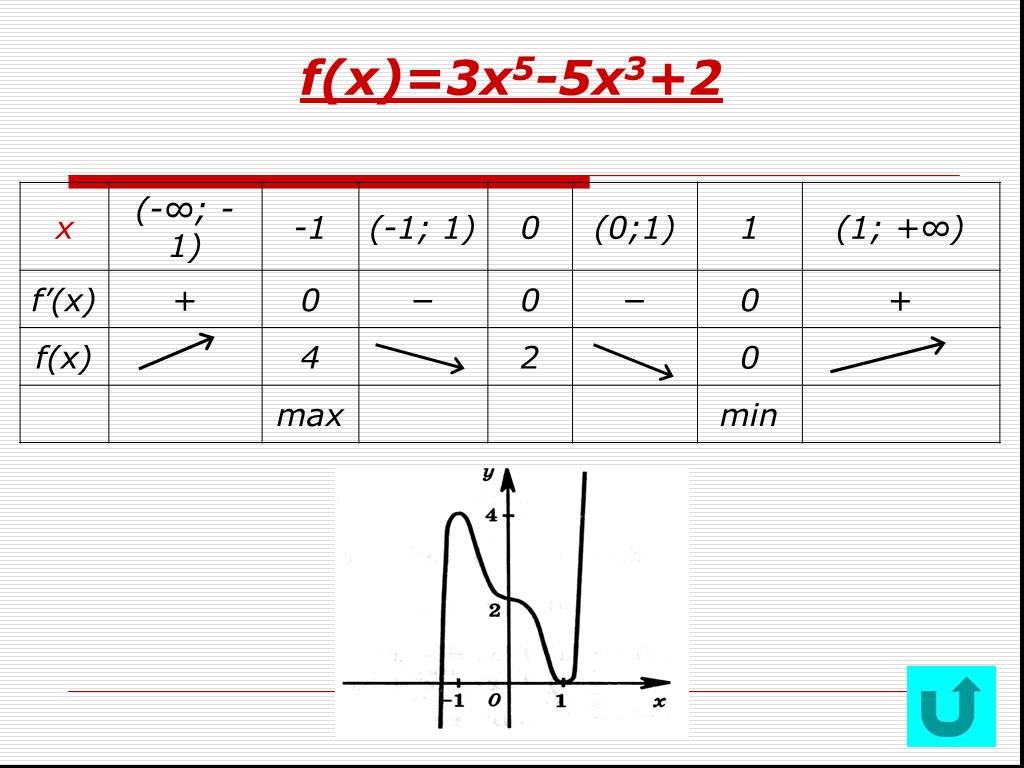
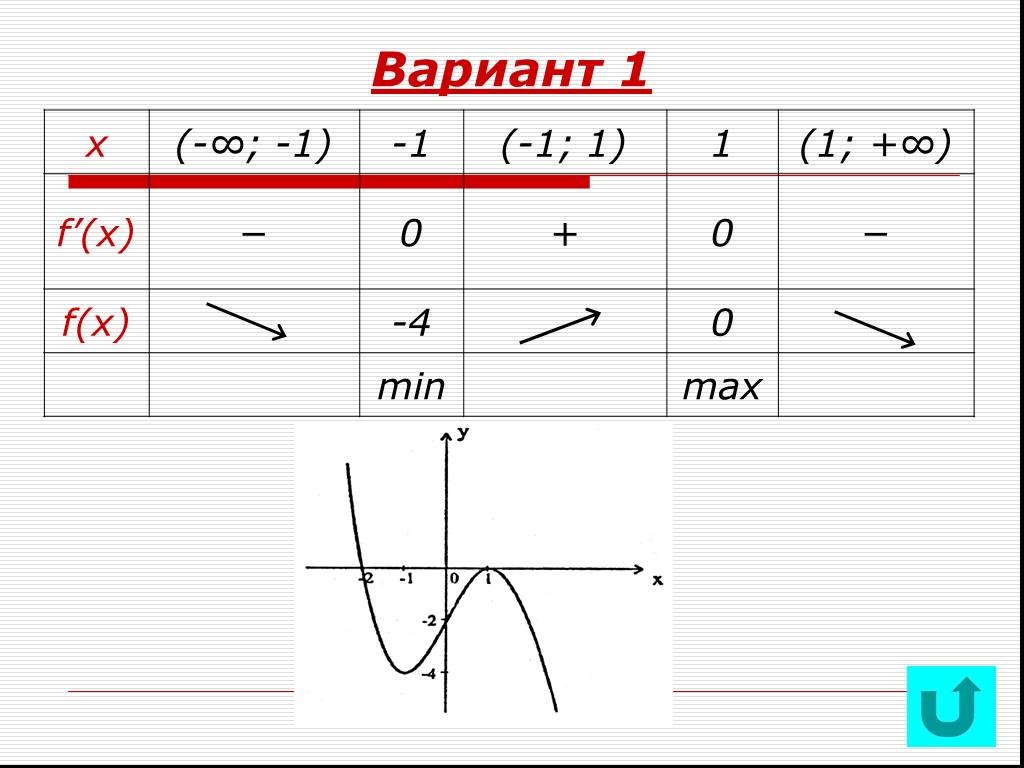
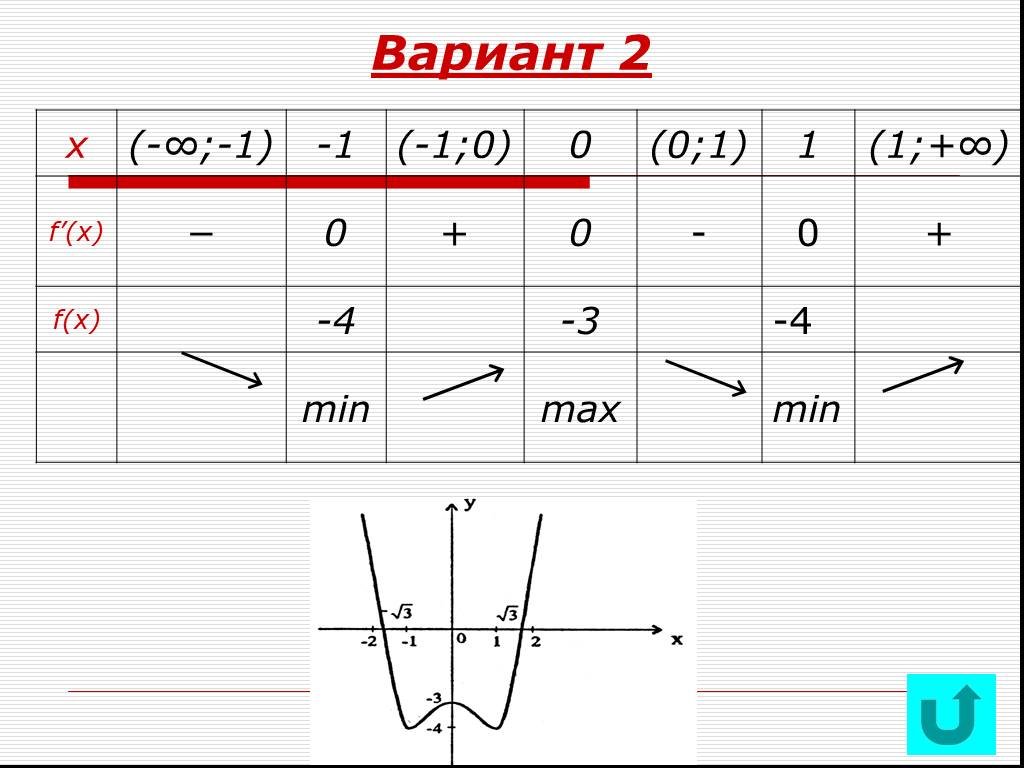
Исследование функции с помощью производной
Правила дифференцирования. Производная суммы равна сумме производных. Постоянный множитель можно вынести за знак производной. Производная произведения ...Исследование функции с помощью производной
Исследование функции с помощью производной. УСТНЫЙ ОПРОС. Достаточный признак возрастания функции. Достаточный признак убывания функции. Какие точки ...Исследование функции и построение графика
ЕГЭ - 2014 Ответ: 3. Ответ: -0,25. Ответ: 7. Ответ: 2. . Ответ: 9. Ответ: 0. Ответ: -2. Ответ: 5. Ответ: 4. Ответ: -3. . Ответ: -12. . Исследование ...Исследование функции производной
Цели урока: выяснение степени усвоения . правил вычисления производных; дать понятие «промежутка монотонности функции» уметь применять производную ...Исследование графика функции с помощью производной.
Задача 1. По графику производной укажите количество промежутков возрастания непрерывной на [-7;4] функции. -7 4 Y=f'(x) проверка 0 1 X Y Y=f‘(x). ...Тригонометрические функции углового аргумента - алгебра,
Тригонометрическая функция углового аргумента. Что будем изучать:. Определение. Примеры. Вспомним геометрию. Градусная мера угла. Радианная мера угла. ...Тригонометрические функции
Содержание. Введение................................................... .......3-5слайд Начало изучения..............................................6-7 ...Свойства функции
1.Определение функции. y= x, n=2 2.Область определения D(y)=[0;+ ). 3.Область значений. E(y)=[0;+ ) 4.Четность не четная и не нечетная. 0. 5.Ноль ...Свойства и график показательной функции
Тема: «Свойства и график показательной функции». Цели урока: Усвоить формулировку определения показательной функции; Научиться исследовать показательную ...Производная сложной функции
Производная сложной функции. Сложная функция. Производная простой функции. Простая функция. Пример:. . . . ...Признаки возрастания и убывания функции
Цель урока. Научить применять производную к определению промежутков монотонности функций, продолжать учить работать в парах, развивать навыки работы ...Построить график функции
Содержание:. 1. Функция y=sin x, её свойства и разновидности; 2. Функция y=cos x, её свойства и разновидности; 3. Примеры задач. 4. Закончить просмотр. ...График квадратичной функции Неравенства с одной переменной
Квадратичная функция и ее график. Квадратичной функцией называется функция, которую можно задать формулой вида y = ax² + bx + c, где х – независимая ...Геометрический смысл производной функции
Рано или поздно всякая правильная математическая идея находит применение в том или ином деле. А.Н.Крылов. Цель урока. 1) выяснить, в чем состоит геометрический ...Вычисление производной функции
При вычислении производной функции, будем иметь в виду, что один из способов найти производную - это взять достаточно малые значения справа и слева ...Возрастание и убывание функции
Числовые промежутки. [α;b] – отрезок (α;b) – интервал (α;b] – полуинтервал [α;b) - полуинтервал. Функция f(x) называется возрастающей на некотором ...Влияние коэффициентов а, b и с на расположение графика квадратной функции
Определите, график какой функции изображен на рисунке:. у = х² – 2х – 1; у = –2х² – 8х; у = х² – 4х – 1; у = 2х² + 8х + 7; у = 2х² – 1. у = ½х² – ...Взаимное расположение графиков линейной функции
Разбейте функции, заданные формулами, на группы:. у = 2х - 3; у = х2 - 3; у = - 5х; у = 4 - 0,5х; у = - х +2; у=15х;. 7. 8. 9. 10. у = х (1 - х). ...Взаимно обратные функции
Задача. у = f (x), x - ! Найти значение у при заданном значении х. Задача. у = f (x), у- ! Найти значение х при заданном значении у. Дано: у = 2х ...Функция. Свойства функции
Cодержание 4. Определение функции. 1 5. Способы задания функции. График функции. Алгоритм описания свойств функции. Свойства функции. 3. Числовой ...Конспекты
Исследование функции с помощью производной
Государственное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №151 Красногвардейского района Санкт-Петербурга. 195426, ...Исследование функции с помощью производной
Опорный конспект. . «Исследование функции с помощью производной. ». ГАОУ СПО ВПТК. Зотова И.В., преподаватель математики. Найти область ...Исследование функции
Яковлева Мария Викторовна. МОУ Приморская СОШ. Челябинская область Агаповский район поселок Приморский. Учитель математики. Урок по теме ...Исследование функции с помощью производной
Выездное заседание республиканского клуба «Пеликан». 20 марта 2012 г. План-конспект урока. Тема «Исследование функции с помощью производной». ...Свойства функции
Управление образования г.Астаны. ИПК и ПК СО. ГУ «Средняя школа № 36». Урок алгебры в 10 классе по теме: «Свойства функции». Подготовила: ...Производная сложной функции
АЛГЕБРА. 10 класс. «Производная сложной функции». Тема. : Производная сложной функции. ...Решение квадратного неравенства с помощью графика квадратичной функции
"Решение квадратного неравенства с помощью графика квадратичной функции". . Цели:. . 1. Повторить знания о квадратичной функции. 2. Познакомиться ...Применение понятия периодической функции
РАЗРАБОТКА УРОКА. учителя математики МОУ гимназии № 35 г.о. Тольятти. Батаевой Галины Александровны. Предмет: алгебра и начала анализа. Класс: ...Применение производной к исследованию функции
Обобщающий урок в 11 классе по теме. «Применение производной к исследованию функции». Цель урока:. Систематизирование и обобщение знаний ...Возрастание и убывание функции
Муниципальное общеобразовательное учреждение. . Копорская средняя общеобразовательная школа. Ленинградской области. КОНСПЕКТ УРОКА. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:2 мая 2019
Категория:Математика
Содержит:18 слайд(ов)
Поделись с друзьями:
Скачать презентацию