Презентация "Из истории обыкновенных дробей" по математике – проект, доклад

МБОУ «Пригородная средняя общеобразовательная школа №1 Оренбургского района»

Из истории обыкновенных дробей Работа учащегося 6 класса Какурина Даниила Руководитель: Рожко И.А.

Есть такая дробь у нас, Про неё пойдет весь сказ, Она из чисел состоит, А между ними, как мосточек, Дробная черта лежит, Над чертою числитель, Знайте, Под чертою – знаменатель, Дробь такую непременно Надо звать обыкновенной.

Объект исследования: История возникновения обыкновенных дробей Предмет исследования: Обыкновенные дроби Гипотеза: Если бы не было дробей – могла бы развиваться математика? 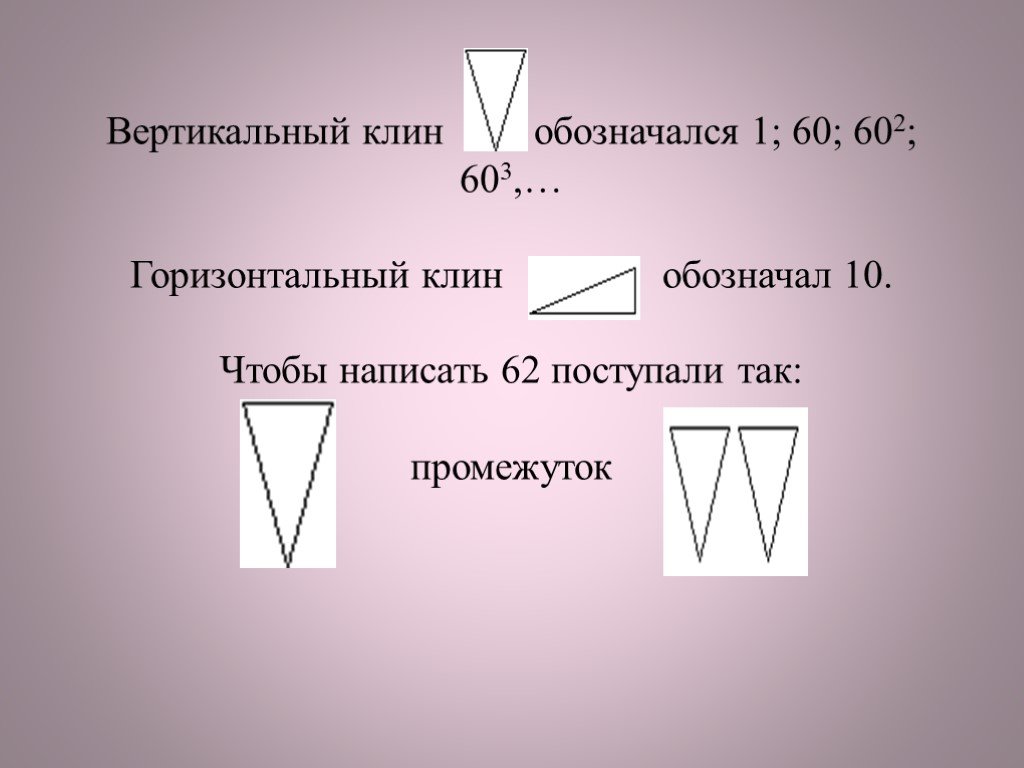Методы исследования: - работа с литературой - поиск информации во всемирной сети Интернет - работа с дробями в игровой форме Цель работы: -расширение знаний о происхождении дробей -изучение последовательности усовершенствования записи обыкновенных дробей Задачи: сделать анализ: -почему дроби записывают таким образом? -кто придумал такие записи? -есть ли их дальнейшее развитие?

На протяжении многих веков на языках народов ломаным числом именовали дробь. Необходимость в дробях возникла на ранней ступени развития человечества. Так, по-видимому, дележ десятка плодов между большим числом участников охоты заставлял людей обращаться к дробям. Первой дробью была половина. Для того, чтобы из одного получить половину, надо разделить единицу, или «разломить» ее на два. От сюда и пошло название ломаные числа. Теперь их называют дробями. Различают три вида дробей: Единичные (аликвоты) или доли (например, 1/2, 1/3, 1/4, и т.д.). Систематические, т.е дроби, у которых знаменатель выражается степенью числа (например, степенью числа 10 или 60 и т.д.). Общего вида, у которых числителем и знаменателем может быть любое число. Существуют дроби «ложные» – неправильные и «реальные» – правильные.

Первым европейским учёным, который стал использовать и распространять современную запись дробей, был итальянский купец и путешественник Фибоначчи (Леонардо Пизанский). В 1202 году он ввел слово дробь.

Дроби в Древнем Египте.

Первой дробью была половина. За ней последовали 1/4,1/8,1/16,…, затем 1/3,1/6, и т.д., т.е. самые простые дроби, доли целого, называемые единичные. Древние египтяне выражали любую дробь в виде суммы только основных дробей. Египтяне писали на папирусах, т.е на свитках, изготовленных из стебля крупных тропических растений, носивших то же название. Важнейшим по содержанию является папирус Ахмеса, названный так по имени одного из древнеегипетских писцов. Рукою которого он был написан. Его длина 544см, а ширина 33 см.

Хранится он в Лондоне, в Британском музее. Он был приобретён в прошлом веке англичанином Риндом и поэтому называется иногда папирусом Ринда. Этот старинный математический документ озаглавлен так: «Способы, при помощи которых можно дойти до понимания всех тёмных вещей, всех тайн, заключающихся в вещах».

Папирус представляет собой собрание решений 84 задач, имеющих прикладной характер; эти задачи относятся к действиям с дробями, определению площади прямоугольника, имеются также арифметические задачи на пропорциональное деление, определение соотношений между количеством зерна и получающегося из него хлеба или пива и т. д. Однако для решения этих задач не даётся никаких общих правил, не говоря уже о попытках каких-нибудь теоретических обобщений.

В Папирусе Ахмеса есть такая задача— разделить семь хлебов между восемью людьми поровну.

Современный школьник скорее всего решал бы задачу так: надо разрезать каждый хлеб на 8 равных частей и каждому человеку дать по одной части от каждого хлеба. А вот как эта задача решена на папирусе: Каждому человеку нужно дать по половине, четверти и восьмушке хлеба. Теперь ясно, что надо 4 хлеба разрезать пополам, 2 хлеба на 4 части и только один хлеб – на 8 частей. И если нашему школьнику пришлось бы сделать 49 разрезов, то Ахмесу – всего 17, т.е. египетский способ почти в 3 раза экономичнее.

Для разложения неединичных дробей на сумму единичных существовали готовые таблицы, которыми и пользовались египетские писцы для необходимых вычислений.

Эта таблица помогала производить сложные арифметические выкладки согласно принятым канонам. По-видимому, писцы заучивали ее наизусть, так же, как сейчас школьники запоминают таблицу умножения. С помощью этой таблицы выполняли и деление чисел. Умели египтяне также умножать и делить дроби. Но для умножения приходилось умножать доли на доли, а потом, быть может, снова использовать таблицу. Еще сложнее обстояло дело с делением.

Вавилон.

В древнем Вавилоне высокий уровень культуры был достигнут в третьем тысячелетии до нашей эры. Шумеры и аккадцы, населявшие Древний Вавилон, писали не на папирусе, который в их стране не рос, а на глине. Путем нажатия клиновидной палочкой на мягкие глиняные плитки наносились знаки, имевшие вид клиньев. Вот почему такое письмо называется клинописью.

Вертикальный клин обозначался 1; 60; 602; 603,… Горизонтальный клин обозначал 10. Чтобы написать 62 поступали так: промежуток

Дроби в Древнем Риме.

Интересная система дробей была в Древнем Риме. Она основывалась на делении на 12 долей единицы веса, которая называлась асс. Двенадцатую долю асса называли унцией. А путь, время и другие величины сравнивали с наглядной вещью - весом. Например, римлянин мог сказать, что он прошел семь унций пути или прочел пять унций книги. При этом, конечно, речь не шла о взвешивании пути или книги. Имелось в виду, что пройдено 7/12 пути или прочтено 5/12 книги. А для дробей, получающихся сокращением дробей со знаменателем 12 или раздроблением двенадцатых долей на более мелкие, были особые названия.

Римская система дробей и мер была двенадцатеричной. Даже сейчас иногда говорят: "Он скрупулезно изучил этот вопрос". Это значит, что вопрос изучен до конца, что ни одной самой малой неясности не осталось. А происходит странное слово "скрупулезно" от римского названия 1/288 асса - "скрупулус". В ходу были и такие названия: "семис" - половина асса, "секстане" - шестая его доля, "семиунция" - полунции, то есть 1/24 асса, и т. д. Всего применялось 18 различных названий дробей. Чтобы работать с дробями, надо было для этих дробей помнить и таблицу сложения, и таблицу умножения. Поэтому римские купцы твердо знали, что при сложении триенса (1/3 асса) и секстанса получается семис, а при умножении беса (2/3 асса) на сескунцию (3/2 унции, то есть 1/8 асса) получается унция. Для облегчения работы составлялись специальные таблицы, некоторые из них дошли до нас.

Древняя Греция.

В греческих сочинениях по математике дробей не встречалось. Греческие ученые считали, что математика должна заниматься только целыми числами. С дробями они предоставляли возиться купцам, ремесленникам, а также землемерам, астрономам и механикам. Но старая пословица говорит: « Гони природу в дверь, она влетит в окно». Поэтому и в строго научные сочинения греков дроби проникали, так сказать « с заднего хода». В Греции употреблялись наряду с единичными, «египетскими» дробями и общие, обыкновенные дроби. Среди разных записей употреблялась и такая: сверху знаменатель, под ним числитель дроби.

Еще за 2-3 столетия до Евклида и Архимеда греки свободно владели арифметическими действия с дробями. В VI в. до н.э. жил знаменитый ученый Пифагор. Рассказывают, что на вопрос, сколько учеников посещают его школу, Пифагор ответил: «Половина изучает математику, четверть – музыку, седьмая часть пребывает в молчании, кроме этого, есть три женщины».

Дроби на Руси.

На Руси дроби называли долями, позднее «ломанными числами» Например, - эти дроби назывались родовые или основными.

Половина, полтина –1 2 Четь – 1 4 Полчеть – 1 8 Полполчеть – 1 16 Пятина – 1 5 Треть – 1 3 Полтреть –1 6

Из истории обозначения дробей.

Современную систему записи дробей с числителем и знаменателем создали в Индии. Только там писали знаменатель сверху, а числитель – снизу и не писали дробной черты. Записывать дроби в точности, как сейчас, стали арабы. В Древнем Китае пользовались десятичной системой мер, обозначали дробь словами, используя меры длины чи: цуни, доли, порядковые, шерстинки, тончайшие, паутинки. Дробь вида 2,135436 выглядела так: 2 чи, 1 цунь, 3 доли, 5 порядковых, 4 шерстинки, 3 тончайших, 6 паутинок. В XV веке, в Узбекистане математик и астроном Джемшид Гиясэддин ал –Каши записал дробь в одну строчку числами в десятичной системе и дал правила действия с ними. Он пользовался несколькими способами написания дроби: то он применял вертикальную черту, то чернила черного и красного цветов.

Старинные задачи с дробями.

В произведении знаменитого римского поэта I века до н. э. Горация так описана беседа учителях учеником в одной из римских школ этой эпохи: Учитель. Пусть скажет сын Альбина, сколько останется, если от пяти унций отнять одну унцию? Ученик. Одна треть. Учитель. Правильно. Ты сумеешь беречь свое имущество. Решение: 4 унции 4 унции 4 унции Ответ: 1/3

Задача из "Папируса Ахмеса" (Египет, 1850 г. до н. э.)

"Приходит пастух с 70 быками. Его спрашивают: - Сколько приводишь ты своего многочисленного стада? Пастух отвечает: - Я привожу две трети от трети скота. Сочти!" Решение: 1) 70:2·3=105 голов - это 1/3 от скота 2) 105·3=315 голов скота Ответ: 315 голов скота

Спасибо за внимание!

Литература

1.История арифметики. Депман,1965г. 2.История математики от Декарта до середины 19 столетия. Вилейтнер, 1960г. 3.Энциклопедия для детей Аванта+ математика. 4.Детская энциклопедия. М.,1965г.