Презентация "Функция. Свойства функции" по математике – проект, доклад
Презентацию на тему "Функция. Свойства функции" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 19 слайд(ов).
Слайды презентации
Список похожих презентаций
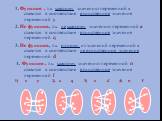
I Функция У=АХ², её график и свойства
А=1 У=Х ². А=2 У=2Х ². У=Х² У=2Х². Растяжение от оси Х в два раза. А=0.5 У=Х² У=0.5Х². Сжатие по оси Х в два раза. Вообще график функции У=АХ² можно ..."Функция y = kx², ее свойства и график". 8-й класс
Траектория движения комет в межпланетном пространстве. Архитектурные сооружения. . Траектория движения. Тема урока. Функция у=кх2, ее график и свойства ...Определение линейной функции
Урок алгебры в 7 классе. Тема урока: Определение линейной функции. введение понятия линейной функции; отработка навыка распознавания линейной функции ...Область определения функции
. . Найдите область определения функции. Цель. Научиться находить область определения функции, заданной аналитически Задачи: построить алгоритм нахождения ...Наибольшее и наименьшее значения функции на отрезке
схема нахождения наибольшего и наименьшего значения функции на отрезке:. 1. Найти производную функции. 2. Найти критические точки, в которых производная ...Логарифмы. Свойства логарифмов
Изобретатель первых логарифмических таблиц, впервые ввёл сам термин «логарифм» шотландский математик Джон Непер. «Я старался, насколько мог и умел, ...Коэффициенты квадратной функции
Предисловие. В данном проекте автор специально не использовал теоретическое обоснование, а только выводы на их основе. Для более глубокого и полного ...Построение графика функции методом ее исследования с помощью производной
доцент кафедры математического образования Батан Любовь Федоровна. учитель математики первой квалификационной категории МОУ лицей № 176 Ткаченко Зоя ...Понятие производной функции
Автор Сизова Н. В., г. Саров. Производная. Историческая справка. Тайны планетных орбит. Древнегреческие учёные умели решать немногие задачи кинематики ...Алгоритмы - их функции и виды
Разветвляющийся алгоритм. Сюда пойдешь – клад найдешь. Сюда пойдешь – жену найдешь. Сюда пойдешь – мегабайт найдешь. Составить блок-схему алгоритма ...Алгоритм. Свойства алгоритма
Алгоритм «Заваривания чая». Вскипятить воду. Окатить заварочный чайник кипятком. Засыпать заварку в чайник. Залить кипятком. Закрыть крышечкой. Накрыть ...Алгоритм построения графика квадратичной функции
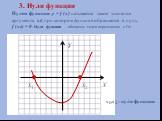
1)направление «ветвей» параболы. если а>0, то «ветви» параболы направлены вверх; если а 0 - «ветви» параболы направлены вверх;. 2)Нахождение координат ...Алгебра функции
Функции. Задания раздела направлены на проверку умений использовать графические представления для ответа на вопросы , связанные с исследованием функций. ...Параллелограмм. Свойства параллелограмма
Проверка домашнего задания. Параллелограмм – это. четырехугольник равны. многоугольник. у которого противоположные стороны попарно. параллельны. Правильно! ...Алгоритмы построения графиков функции
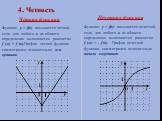
График функции у = |х| а) Если х≥0, то |х| = х функция у = х, т.е. график совпадает с биссектрисой первого координатного угла. б) Если х. Построить ...Понятие о комплексных числах. Рациональные функции одной переменной
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Спасибо за внимание. ...Взаимно обратные функции
Цель проекта: Изучить поведение взаимно обратных функций. Установить связь графиков прямой и обратной функций. Подготовиться к успешной сдаче ЕГЭ. ...Понятие функции
План. Различные подходы к определению понятия функция Методика введения понятия функции в учебниках различных авторов Методические особенности изучения ...Взаимно обратные функции
Задача. у = f (x), x - ! Найти значение у при заданном значении х. Задача. у = f (x), у- ! Найти значение х при заданном значении у. Дано: у = 2х ...Как построить график функции у = mf(x),если известен график функции у = f(x)
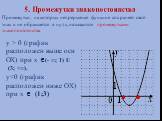
Вид преобразования: параллельный перенос. у = х у = 2х у =½х. у = 4х у =¼х. у =½x² у =2 х². у=5х² у = х². что произойдет с графиками при умножении ...Конспекты
Логарифмическая функция. График и свойства логарифмической функции
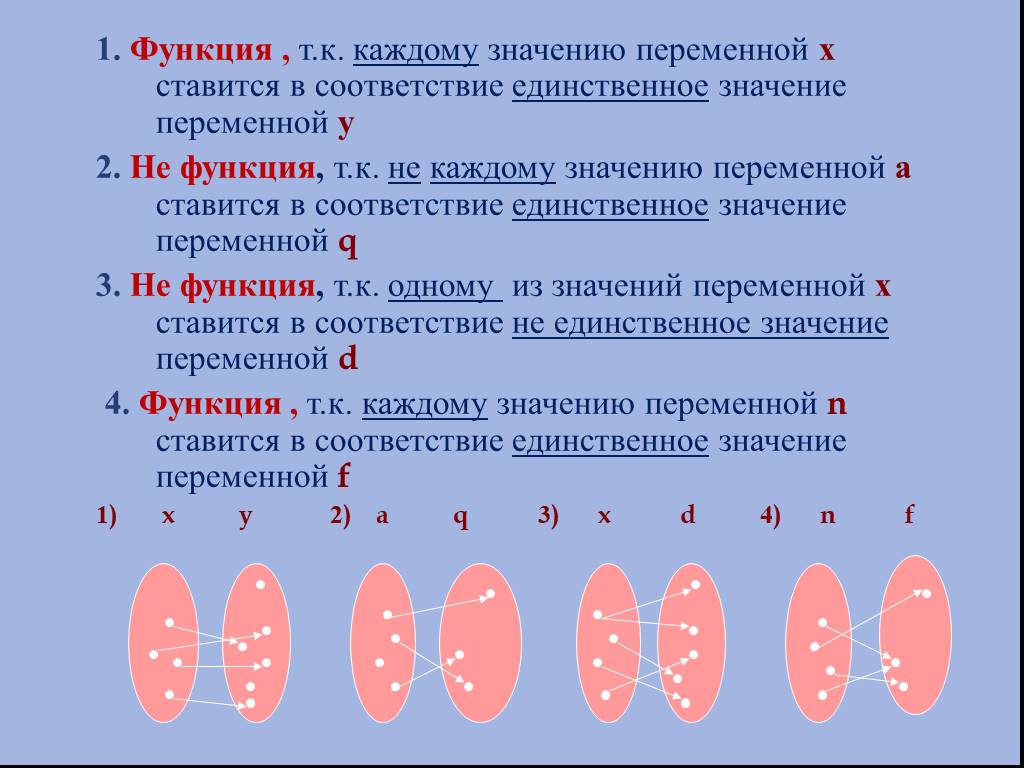
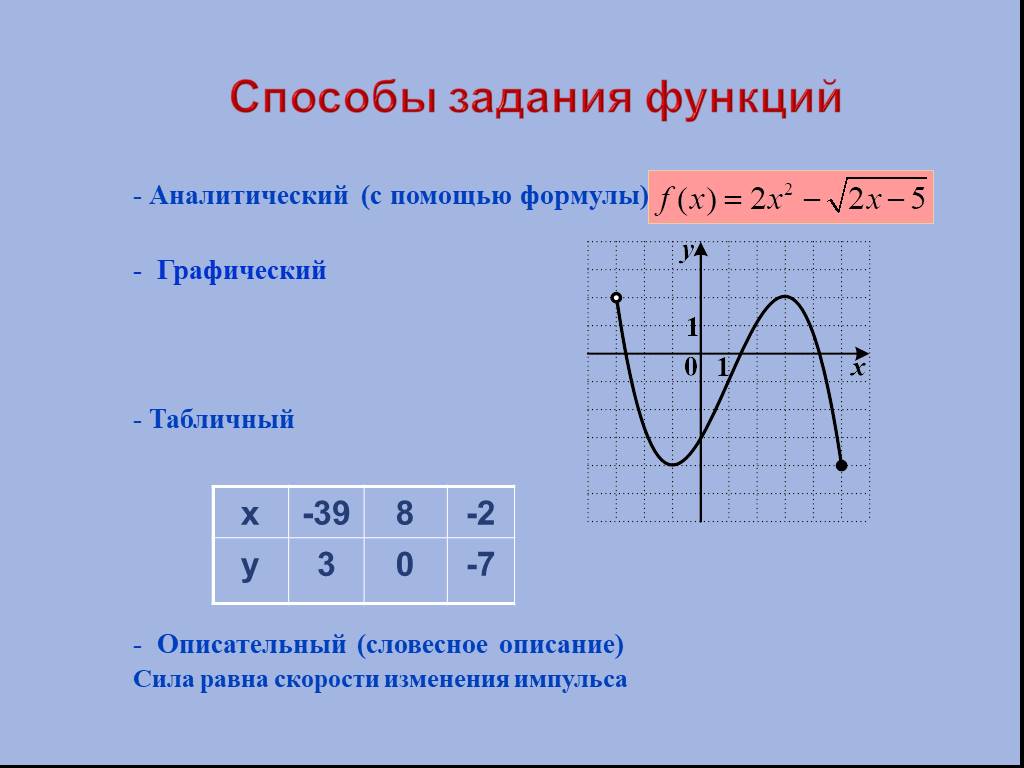
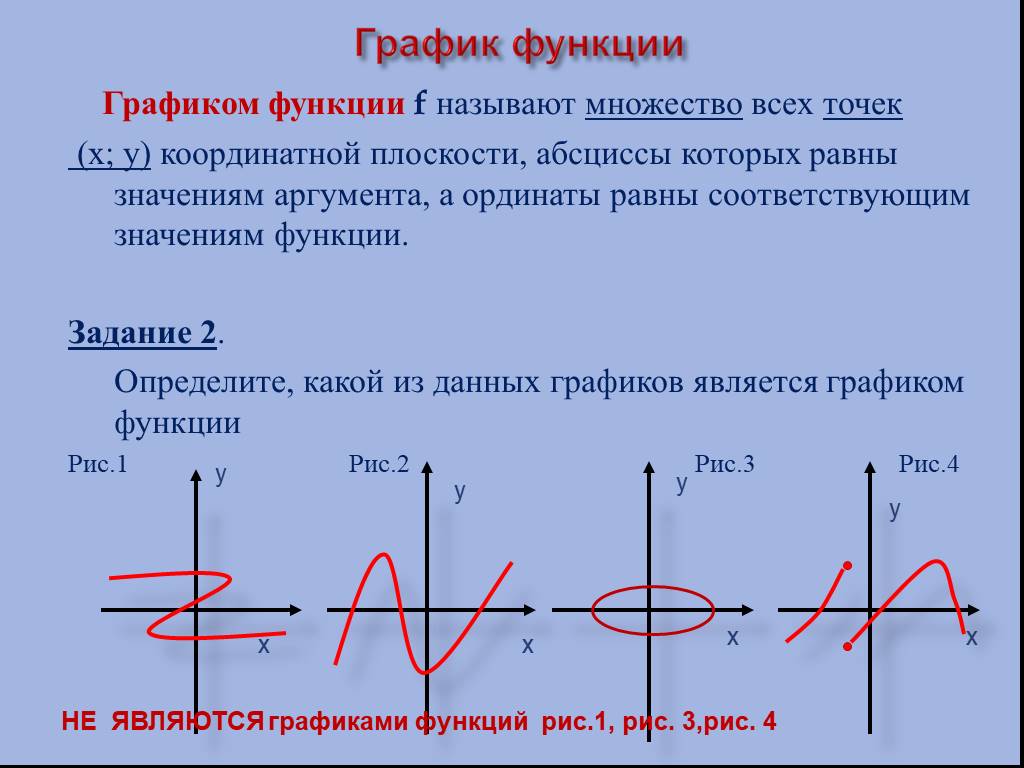
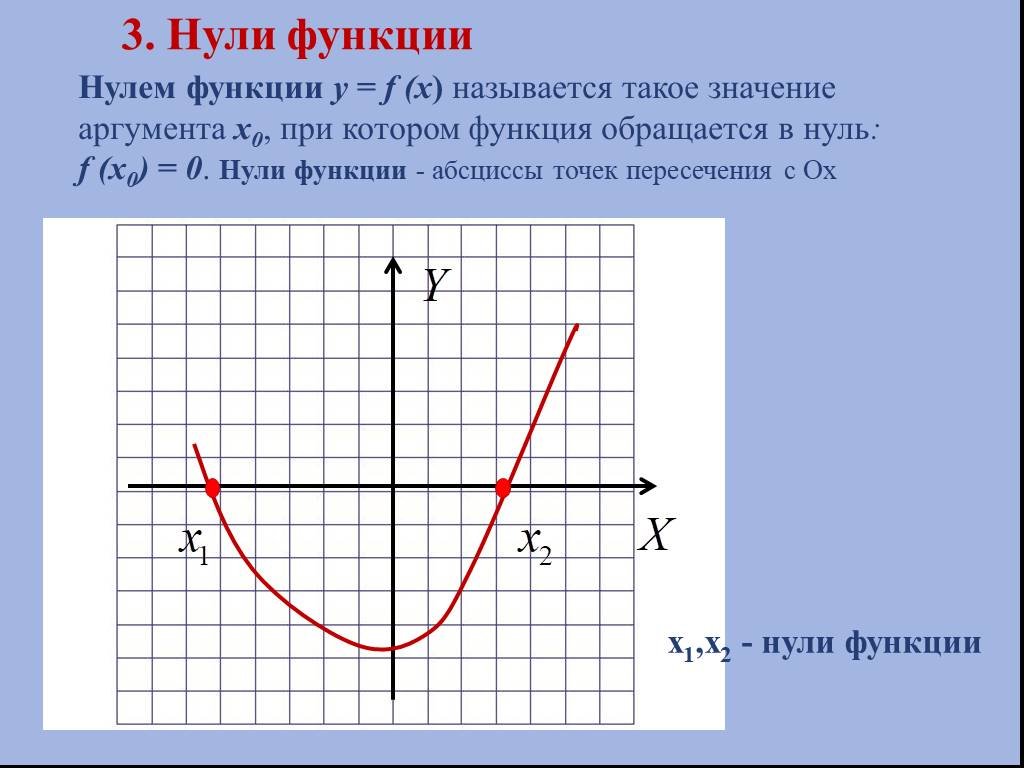
Класс: 11. Тема урока. : Логарифмическая функция. График и свойства логарифмической функции (Слайд 1,2). Цели урока:. . 1.Ввести определение ...Общее понятие функции, способы её задания, свойства функции
Методическая разработка урока математики по теме. «Общее понятие функции, способы её задания, свойства функции». Пояснительная записка. Преподаватель: ...Свойства линейной функции
Государственное бюджетное образовательное учреждение. средняя общеобразовательная школа №200 с углубленным изучением финского языка. Красносельского ...Предел функции в точке, свойства. Бесконечно большие и бесконечно малые функции. Непрерывность функции
Министерство образования и науки Самарской области. . ГБОУ СПО «Безенчукский аграрный техникум». Конспект занятия. ТЕМА. Предел функции ...Определение числовой функции. Виды. Свойства, графики числовых функций. Способы задания функции
Кейс технологии. Урок алгебры. . Калинина Ирина Борисовна. учитель математики. МАОУ ГИМНАЗИЯ №8 г. Перми. РАЗРАБОТКА УРОКА. c. применением ...Свойства показательной функции. Решение показательных уравнений и неравенств
Открытый урок по теме: «Свойства показательной функции. Решение показательных уравнений и неравенств.». Тип урока:. Обобщение и систематизация ...Квадратичная функция. Построение графика квадратичной функции
Конспект урока. Тема урока:. Квадратичная функция. Построение графика квадратичной функции . Класс:. 8. Цели урока:. . . 1. Формирование ...Свойства арифметического квадратного корня
Муниципальное бюджетное общеобразовательное учреждение. основная общеобразовательная школа № 8. поселка Садового муниципального образования Славянский ...Производная сложной функции
АЛГЕБРА. 10 класс. «Производная сложной функции». Тема. : Производная сложной функции. ...Решение квадратного неравенства с помощью графика квадратичной функции
"Решение квадратного неравенства с помощью графика квадратичной функции". . Цели:. . 1. Повторить знания о квадратичной функции. 2. Познакомиться ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:28 января 2019
Категория:Математика
Содержит:19 слайд(ов)
Поделись с друзьями:
Скачать презентацию