Презентация "Метод областей" по математике – проект, доклад
Презентацию на тему "Метод областей" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 40 слайд(ов).
Слайды презентации
Список похожих презентаций
Методы решений заданий С5. Метод областей в решении задач
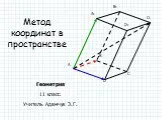
(«переход» метода интервалов с прямой на плоскость). 1. Область определения 2. Граничные линии 3. Координатная плоскость 4. Знаки в областях 5.Ответ ...Решение неравенств с параметрами методом областей
«Но когда эти науки (алгебра и геометрия) объединились, они энергично поддержали друг друга и быстро зашагали к совершенству». Ж.А. Лагранж. АКТУАЛЬНОСТЬ ...Метод координат
Рене Декарт (1596-1650). Французский математик, физик, философ, создатель знаменитого метода координат, сторонник механизма с физике, предтеча рефлексологии. ...Метод Гаусса и Крамера
Содержание. Что такое матрица? Карл Фридих Гаусс Метод Гаусса Габриэль Крамер Метод Крамера Вывод Использованные источники информации. Матрица Определение. ...Применения непрерывности Метод интервалов
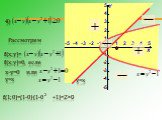
Задания для групп. Группа 1 а) (х-2)3(х+1)((х-1)(х2+2х+5)0 б) в) Группа 3 а) (х+4)2(х+5)2(х-6)(х+3)≤0 б) в). ответы. 1группа а) (-1;1),(1;2); б) (-5;-1),(2;3),(3;+∞); ...Метод площадей при решении геометрических задач
Cодержание. Введение. В элементарной математике, самыми трудными считаются геометрические задачи. При решении геометрических задач, как правило, алгоритмов ...Метод математической индукции
Содержание: 1.Введение. 2.Основная часть и примеры. 3.Заключение. Введение В основе всякого математического исследования лежат дедуктивный и индуктивный ...Метод координат на плоскости
1. Координатная ось. Координатной осью называется прямая, на которой отмечена точка О (начало отсчета или начало координат), выбран масштаб, т.е. ...Метод интервалов решения неравенств
Решение неравенства. Решением неравенства с неизвестным х называют число, при подстановке которого в это неравенство вместо х получается верное числовое ...Метод интервалов
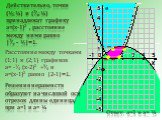
Рассмотрим функцию f(х)=(х+3)(х-1)(х-2). D(f)- любое число, нули функции- числа -3; 1; 2. Нули функции разбивают всю область определения на промежутки: ...Метод интервалов
Устная работа. На рисунке изображен график функции.Используя график, решите неравенство. Для каждой функции, заданной формулой, укажите ее график. ...
Метод интервалов
Корни многочлена делят числовую ось на промежутки, на каждом из которых функция сохраняет свой знак без изменения - либо везде положителен, либо отрицателен. ...Метод золотого сечения
Золотая пропорция – гармония и красота. Выполнили учащиеся 9 класса: Ларина Екатерина, Морозов Дмитрий, Кочеткова Яна, Петрович Денис и др. Гармоничны ...Метод графов
Введение. Графы заинтересовали нас своей возможностью помогать в решении различных головоломок, математических и логических задач. Так как мы участвуем ...Метод Гаусса решения систем линейных уравнений
Рассмотрим систему m линейных уравнений с n неизвестными:. Назовем матрицей системы матрицу, составленную из коэффициентов при неизвестных. Матрицу, ...Метод координат в пространстве
Цели урока:. 1.Повторить понятия вектора; 2.Ввести понятие прямоугольной системы координат в пространстве. Задачи урока: выработать умения строить ...Метод координат в пространстве
Распознай формулы. Решите задачи. A B C D. ...Метод интервалов. Общий метод интервалов
Литература С.М. Никольский «Алгебра и начала анализа: Учебник для 10 класса общеобразовательных учреждений» §2 п. 2.7 – 2.9. . Определение. . . + ...Метод Мажорант и его применение
Определение. Мажорантой данной функции f(х) на множестве Р, называется такое число М, что либо f(х) ≤ М для всех х ϵ Р, либо f(х) ≥ М для всех х ϵ ...Метод кейсов
Определение. Метод кейсов – это обучение посредством пакета ситуаций для принятия решений, то есть изучение предмета путём рассмотрения большого количества ...Конспекты
Формы представления информации. Метод координат
Автор:. Коджамонян Оксана Игоревна. Должность. : учитель информатики. Место работы. : МБОУ СОШ 30 посёлка Молодёжного муниципального образования ...Метод перебора
Учитель математики Епифанова Т. Н. Проблемно – диалогический урок в 5 классе. . . Тема: Метод перебора. . Учитель. Ученики. ...Системы линейных уравнений. Метод Гаусса
ГБОУ средней общеобразовательной школы №618 г. Москвы. Конспект урока. по теме. «Системы линейных уравнений. Метод Гаусса». ...Метод интервалов
Урок по теме "Метод интервалов ", 9-й класс. Цели:. Деятельностная цель:. формирование умений применением метода интервалов при решении простейших ...Метод координат на плоскости. Координаты на прямой
Муниципальное бюджетное общеобразовательное учреждение. «Вечерняя сменная средняя общеобразовательная школа при ИУ». Конспект урока. Метод координат ...Метод интервалов
Урок по теме "Метод интервалов". Цель:. Рассмотрение метода интервалов и его использование для решения квадратных неравенств, неравенств, связанных ...Метод интервалов
Конспект урока алгебры в 10-м классе. Сизых Галины Дмитриевны. учителя математики МБОУ. «Качульская средняя. . общеобразовательная школа». ...Метод интервалов
Филиал МОУ Петряксинская СОШ- Ново-Мочалеевская ООШ. Разработка урока. . «Метод интервалов». 8 класс. Урок разработан учителем ...Метод введения новой переменной
Алгебра 8 «б» класса. Тема урока :. Метод введения новой переменной. Образовательная. - закрепить навыки решения квадратных уравнений и заданий, ...Метод алгебраического сложения
Тема. Метод алгебраического сложения. Данный урок – изучение нового материала (урок первичного предъявления новых знаний). Цель:. 1. Сформулировать ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Математика
Автор презентации:ученицы 10 класса Сафина Алина и Харламова Анастасия
Содержит:40 слайд(ов)
Поделись с друзьями:
Скачать презентацию
















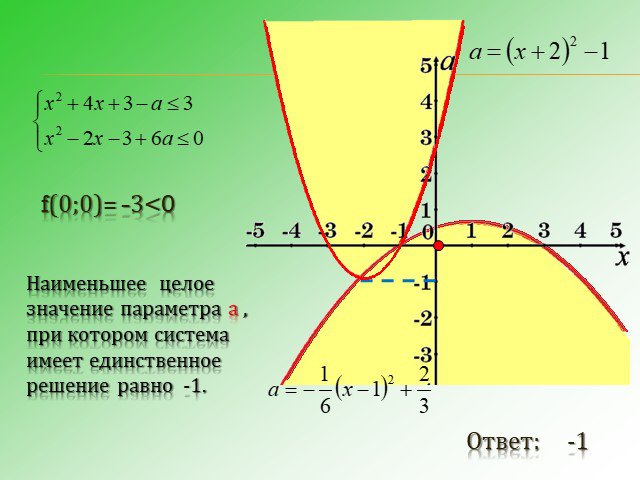


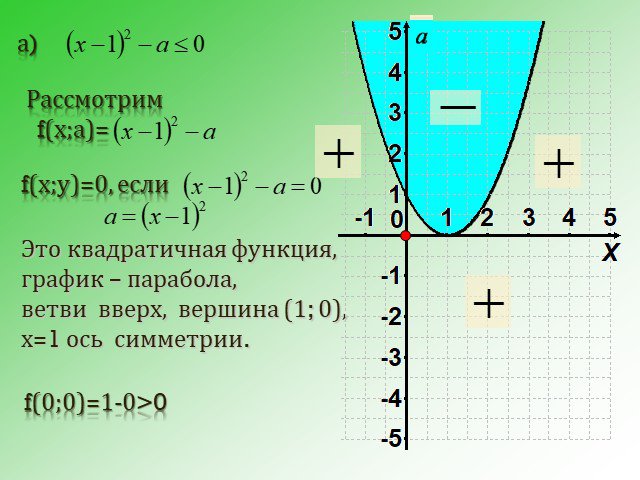

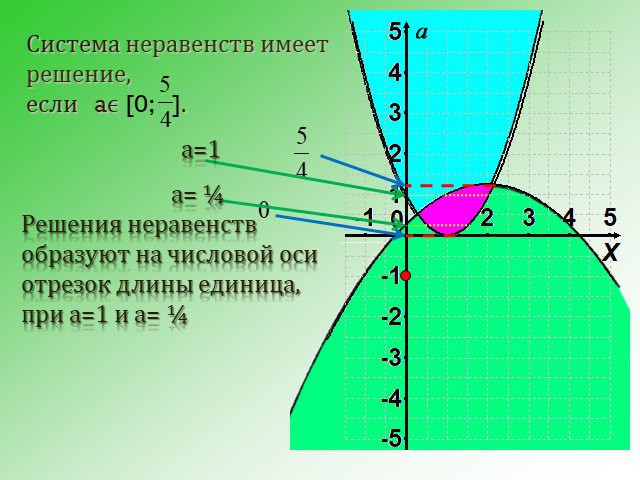
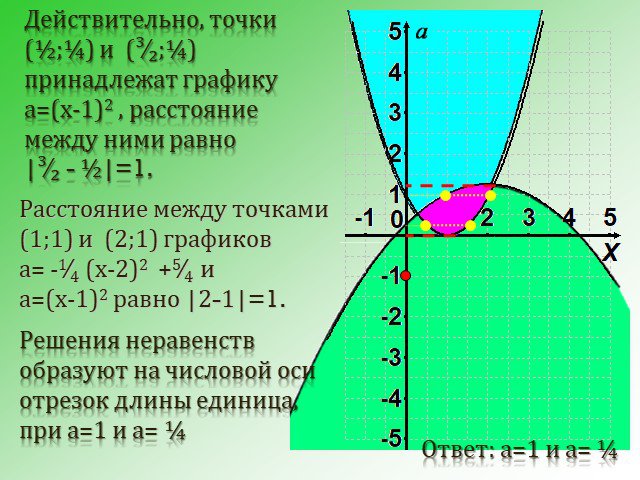


























![Система неравенств имеет решение, если aϵ [0; ]. Решения неравенств образуют на числовой оси отрезок длины единица, при а=1 и а= ¼. а=1 а= ¼ Система неравенств имеет решение, если aϵ [0; ]. Решения неравенств образуют на числовой оси отрезок длины единица, при а=1 и а= ¼. а=1 а= ¼](https://prezentacii.org/upload/cloud/14/09/6246/images/thumbs/screen30.jpg)