Презентация "Метод площадей при решении геометрических задач" по математике – проект, доклад
Презентацию на тему "Метод площадей при решении геометрических задач" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 19 слайд(ов).
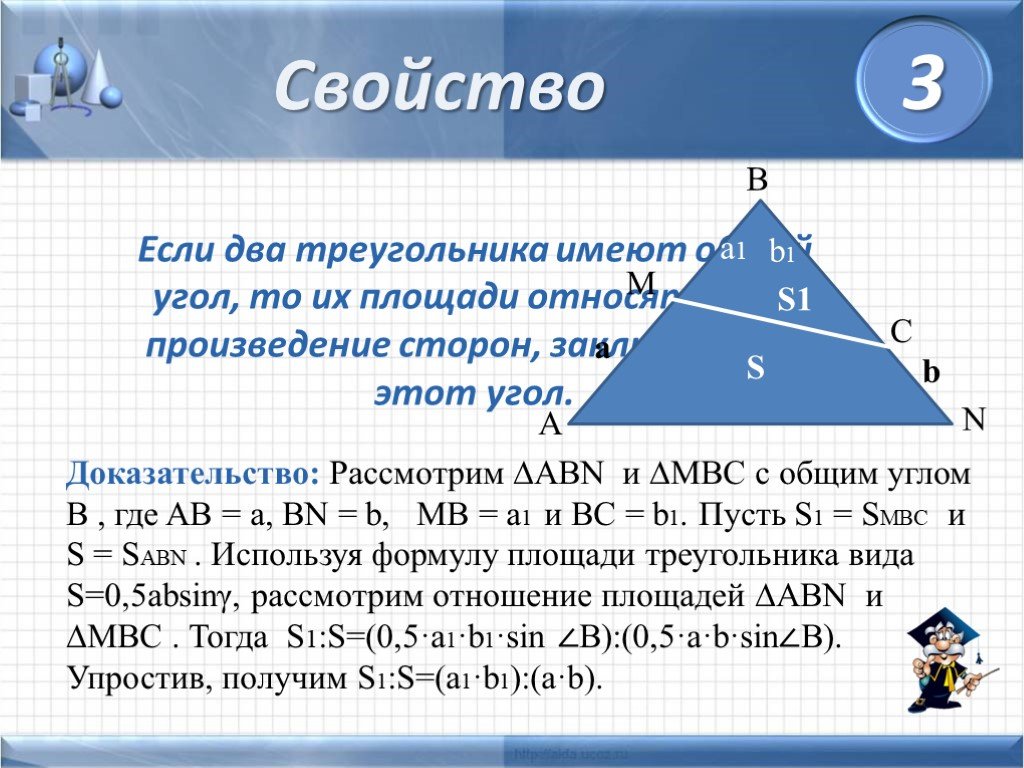
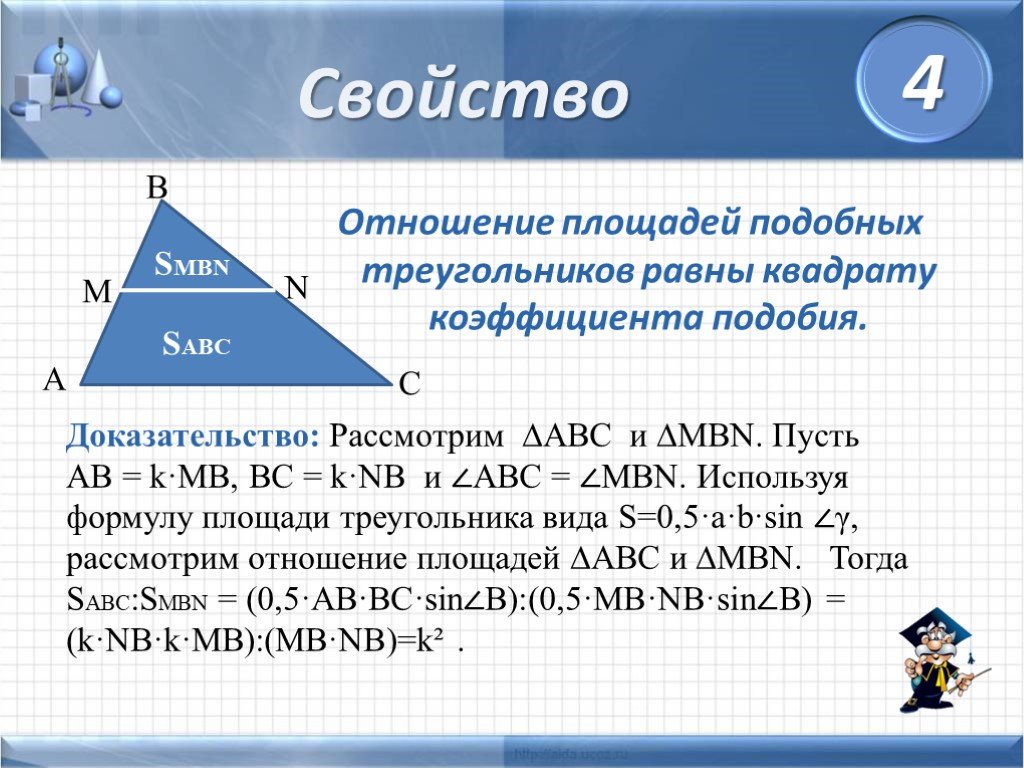
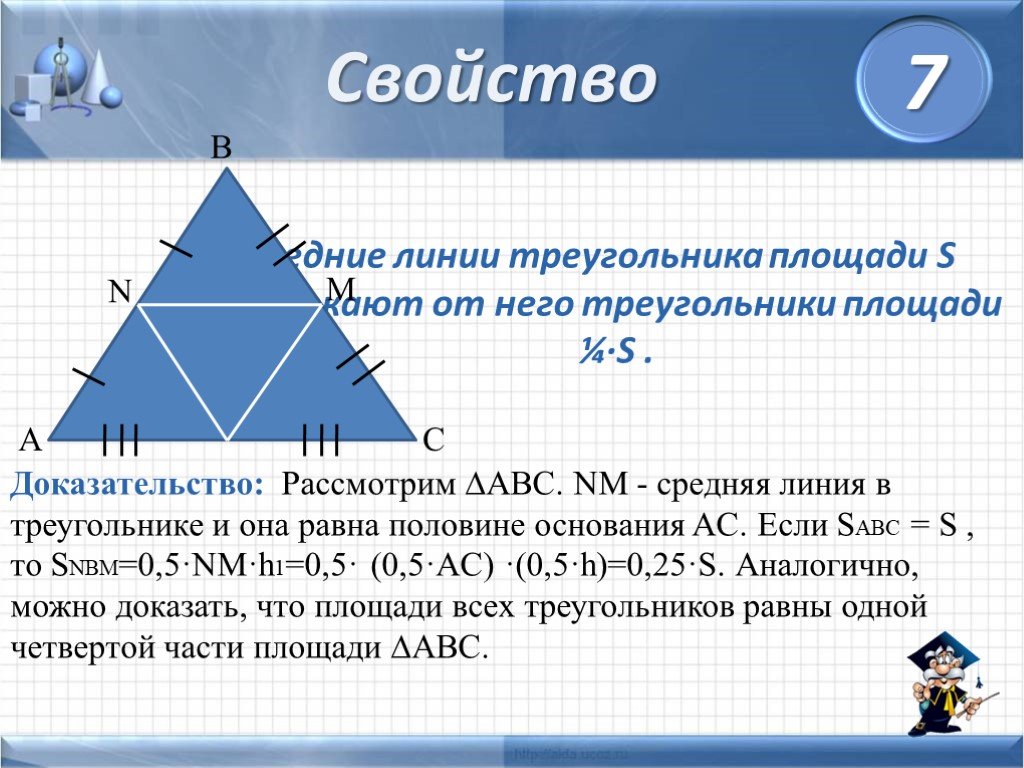
Слайды презентации
Список похожих презентаций
Арифметическая и геометрическая прогрессии при решении задач
с и п о г р я е. ПРОГРЕССИЯ. арифметическая аn+1=аn+ d an= a1+d(n-1). геометрическая bn+1= bn * q bn= b1*qn-1. Арифметическая и геометрическая прогрессии ...Дополнительные построения в трапеции при решении задач
Трапеция – четырёхугольник, две противоположные стороны которого параллельны между собой, а две другие не параллельны. Параллельные стороны трапеции ...Выбор действий при решении задач
Прочитай вопрос и выбери действие. Приношу свои извинения, но придётся начать заново! - · : +. На сколько 25 больше 5? У Лены 5 игрушек. У Вали в ...Графические приемы решения задач с параметрами
Решение уравнений и неравенств, содержащих параметры, является одним из самых трудных разделов элементарной математики. Для их решения обычно требуются ...Графы и их применение к решению задач
Как известно, умение решать задачи является одним из основных показателей уровня математического развития, глубины освоения учебного материала. Поэтому ...ГИА-2012. Решение планиметрических задач на нахождение углов геометрических фигур
1 3 4 5 6 7 8 9 10 11. Вашему вниманию представлено двенадцать прототипов задачи № 11 Открытого банка заданий по математике. ГИА – 2012. Два острых ...Вычисление площадей с помощью интегралов
Знаем:. 1.Как вычислить интеграл. 2. Что такое криволинейная трапеция. 3. Как связаны площадь криволинейной трапеции с интегралом. Криволинейной трапецией ...«Решение задач по математике»
10 февраля. В классе. Задача условие вопрос решение ответ. Быстро и правильно считать. Правильно записывать решение задачи. Кричать и сердиться, когда ...Вычисление площадей плоских фигур с помощью определенного интеграла
ВЫЧИСЛИТЕ ОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ И ВЫ УЗНАЕТЕ ОДНО ИЗ ВЫСКАЗЫВАНИЙ ФРАНЦУЗСКОГО МАТЕМАТИКА С.Д.ПУАССОНА. Жизнь украшается двумя вещами: занятием математикой ...Единицы измерения площадей
Вот как это выглядит. А как за рубежом. В Англии и США до сих пор используется «ступня» - фут ( 31 см), « большой палец» - дюйм ( 25 мм и даже ярд ...Единицы измерения площадей
Устно: Вычислите площадь фигуры. 4дм 2дм 8 дм 4 дм 6 дм. Устно: Вычислите площадь фигуры. А В С Д 4 2 1. Вычислите площадь фигуры. 3 6. Вычислите ...Алгебра высказываний. Решение логических задач
Задача 1: Составьте сложное высказывание в словесной форме из простых, заданных математическим формулировкам:. Высказывание А: «Учащийся Иванов хорошо ...Активизация познавательной деятельности при обучении математике
. Народная Классическая Педагогическая Цирковая (эстрадная) Спортивная. Группировка Классификация Систематизация Ассоциация Аналогия Рифмитизация ...Вектор решение задач
Выразить векторы AM, DA, CA, MB, CD через вектор a и вектор b. № 1 Выразить векторы ВС, CD, AC, OC, OA через векторы а и b. Тивякова Л.А. № 2 Выразить ...ГИА-2012. Решение задач по теме "Чтение графиков функций"
График какой из приведенных ниже функций изображен на рисунке? Задание 17 (№ 197785). Задание 17 (№ 193087). Задание 17 (№ 197695). Задание 17 (№ ...Ассоциация, как помощник, при изучении математики
Ассоциация- это мысленная связь между двумя образами. Чем многообразнее и многочисленнее ассоциации, тем прочнее они закрепляются в памяти. Странные, ...Бинарный урок геометрии и информатики "Четырехугольники. Решение задач" Лауреат
Проверка домашнего задания. В трапеции АВСD (АD – большее основание) диагональ АС ┴СD и делит ВАD пополам, СDА=60, периметр трапеции – 20 см. Найдите ...Аксиомы стереометрии и их следствия. Решение задач
Цель урока: обобщение и применение аксиом и их следствий к решению задач. Математический диктант. 1). Сформулируйте аксиомы стереометрии: Аксиома ...Алгоритм решения простых задач
. ЗАДАЧА условие Вопрос, задание. Работа в парах. 1. Налетело 5 гусей-лебедей, подхватили и унесли братца Иванушку. 2. Печка испекла девять ржаных ...Алгоритм решения задач на пропорции
Эпиграф: «Математика обладает двумя великими сокровищами. Первое-это теорема Пифагора, второе-деление отрезка в крайнем и среднем отношении.» Иоганн ...Конспекты
Закрепление вычислительных навыков при решении нестандартных задач
Урок математики в 4-м классе. Тема: ". . Закрепление вычислительных навыков при решении нестандартных задач". . . . Автор: Витязева ...Закрепление первоначальных приёмов умножения. Решение обратных задач
Открытый урок по математике во 2 «б» классе,. учитель Заруба Наталья Сергеевна. средняя школа № 96 г. Краснодар. Тема: Закрепление первоначальных ...Закрепление решения примеров и задач в пределах 20
Муниципальное казенное специальное (коррекционное) образовательное учреждение для обучающихся, воспитанников с ограниченными возможностями здоровья ...Закрепление решения примеров, простых и составных задач на табличное умножение и деления до 5
Абросимова Марина Владимировна. МБОУ «СОШ№1» г. Топки. . . Учитель начальных классов. Урок математики 3 класс. . Тема. ...Геометрическое решение негеометрических задач
Урок по теме:. «Геометрическое решение негеометрических задач». Сивак Светлана Олеговна. учитель математики. высшей категории. Гимназии №56. ...Закрепление изученного материала. Решение задач и примеров в пределах 100.
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа № 64 ». города Астрахани. Конспект урока ...Закрепление знаний, умений и навыков при прибавлении и вычитании числа 3
Викс Татьяна Юрьевна. МБОУ СОШ № 42 г. Читы. Учитель начальных классов. «Конспект урока по теме: Закрепление знаний, умений и навыков при ...Закрепление знаний о геометрических фигурах
Тема урока. : «Закрепление знаний о геометрических фигурах». Цели урока. :1. Закрепить знания о геометрических фигурах;. 2.Научить решать примеры ...Закрепление вычислительных навыков при сложении и вычитании двузначных чисел
Обобщающий урок по теме: "Закрепление вычислительных навыков при сложении и вычитании двузначных чисел". Урок – путешествие. по фрагментам из современного ...Закрепление .Сложение и вычитание в пределах 10. Решение задач
Путешествие в сказку. Урок математики в 1 классе по теме: «Закрепление .Сложение и вычитание в пределах 10. Решение задач». Цели: закрепить знания ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:12 марта 2019
Категория:Математика
Содержит:19 слайд(ов)
Поделись с друзьями:
Скачать презентацию