Презентация "Метод координат на плоскости" по математике – проект, доклад
Презентацию на тему "Метод координат на плоскости" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 30 слайд(ов).
Слайды презентации
Список похожих презентаций
Астрономия на координатной плоскости
Цели урока:. Закрепить полученные знания и навыки. Проявить творчество при изучении данного раздела. Избежать трудностей при изучении темы «Функция» ...Алгоритмы работы на координатной плоскости
Цели:. Формировать умение работать на координатной плоскости как с положительными, так и отрицательными координатами. Развивать алгоритмическое мышление. ...Алгебраические кривые в полярной системе координат и их применение в природе и технике
Цель: познакомиться с кривыми, не изучаемыми в школьном курсе алгебры, найти для них примеры в природе и технике. Локон Аньези. плоская кривая, геометрическое ...Активные методы обучения на уроках математики и во внеурочной деятельности
Активные методы обучения — это методы, которые побуждают учащихся к активной мыслительной и практической деятельности в процессе овладения учебным ...введение декартовых координат в пространстве
Рене Декарт. x y z 0 1 Ox Oy Oz Ox – ось абсцисс Oy – ось ординат Oz – ось аппликат Координатные оси:. Выберем в пространстве три попарно перпендикулярные ...Взаимное расположение прямой и окружности на плоскости
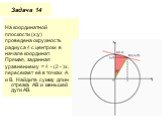
Прямая и окружность пересекаются. d R. d- расстояние от центра окружности до прямой R- радиус окружности. О А В d. Прямая и окружность касаются. d=R. ...Векторы на плоскости
Аналитическая геометрия. Алгебраические поверхности и линии на плоскости первого порядка. Опр. Геометрическое место точек в пространстве (на плоскости) ...Взаимное расположение прямых на плоскости
Цели:. Обобщить знания о прямых на плоскости из алгебры и геометрии 7 класса. Выяснить взаимное расположение прямых, заданных уравнением y=kx+b в ...Аксиомы расположения точек на прямой и плоскости
Выполните действия и сделайте записи:. 1. Изобразите точку С, лежащую на прямой а. 2. Изобразите точку D, не лежащую на этой прямой. 3. Проведите ...«Моя математика» - задачи на нахождение целого или части
МАТЕМАТИКА 1 3 4 5 7 6 8 9 0. Работа с числовым рядом. http://www.bajena.com/ru/kids/mathematics/sum-mathematics.php. 1. Прочитайте текст справа и ...Бумажные складные модели и их использование на уроках геометрии в 10 классе
Модель 1 – «Две пересекающиеся плоскости». Согнутый пополам лист бумаги служит моделью двух пересекающихся плоскостей. Линия сгиба – прямая их пересечения. ..."Разрезание геометрических фигур на части"
ЗАДАЧИ НА РАЗРЕЗАНИЯ. Теорема Бойяи-Гервина гласит: любой многоугольник можно так разрезать на части, что из этих частей удастся сложить квадрат. ...Арифметика Л.Ф. Магницкого. Задачи на сплавы и смеси
Цели моей работы. Познакомиться с биографией Леонтия Филипповича Магницкого Научиться решать задачи на сплавы, находить процентное содержание веществ ..."Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
1. Найти наибольшее значение функции по её графику на [ -5;6] и [-7; 6]. 5 4 -5 у наиб. = 4 [-5; 6] у наиб. = 5 [-7; 6] 1. 2. Найти наименьшее значение ...Влияние коэффициентов на расположение параболы
Цель:. Исследовать зависимость свойств параболы от ее коэффициентов. Задачи:. Выяснить закономерность расположения вершин параболы. Рассмотреть некоторые ...«Задачи на проценты»
Тема урока: Проценты. Тип урока: урок обобщения и систематизации знаний. Цели урока: Образовательные: Обобщение и систематизация знаний учащихся о ...«Старая сказка на новый лад»
3 268 :2 12 396:3 256 130:5 1634 51226. Полетели стрелы в разные стороны. Упала стрела царевича на царский двор. 1634 м. Стрела второго царевича улетела ...Введение понятий "больше‒меньше" на числовом луче
1 0 5 меньше левее. 8 больше правее. 3 3 < 5 < 8 8 > 5 > 3. 3 + 5 =. . . ...Активизация мыслительной деятельности на уроках математики
Активные формы урока. Урок-лекция. Урок-консультация. Урок-практикум Урок-семинар Урок-зачёт. урок-лекция. Зачёт №2 по геометрии в 11 классе 1.Объясните, ...Автоматизация труда учителя на примере решения систем алгебраических уравнений с использованием программного пакета MATHCAD
Ознакомить учителей математики с возможностями продукта MathCAD Обеспечить автоматизацию работы учителей с использованием MathCAD Рассмотреть решение ...Конспекты
Астрономия на координатной плоскости
Леткова Татьяна Викторовна,. учитель математики. Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа ...Декартовы координаты на плоскости
Обобщающий урок по геометрии "Декартовы координаты на плоскости". . Цель урока:. . . истематизировать и обобщить теоретический материал ...Вывод формул для вычисления координат вершины параболы
Нагаева Светлана Николаевна, учитель математики МАОУ « Лицей №1» города Березники. Проект. урока по алгебре в 9 классе. (гуманитарный профиль). ...Векторы на плоскости
. Конспект. обобщающего урока по теме «Векторы на плоскости». . (геометрия 9 класс). Тема. Систематизация и обобщение изученного материала ...Деление и умножение суммы на число
Спресова Наталья Николаевна. Муниципальное общеобразовательное учреждение: средняя общеобразовательная школа, с.Нялинское Ханты-Мансийского района ...Деление десятичных дробей на натуральные числа
МБОУ СОШ № 162. Открытый урок по математике в 5 классе. по теме « Деление десятичных дробей на натуральные числа. Учитель: Титкова Наталья ...Деление десятичной дроби на натуральное число
Азарова Лидия Васильевна, учитель математики МБОУ Михейковская СОШ. Тема:. «Деление десятичной дроби на натуральное число». Класс:. 5. . Тип ...Деление десятичной дроби на десятичную дробь
Урок математики для 5 класса на тему «Деление десятичной дроби на десятичную дробь». План-конспект урока математики в 5 классе по теме "Деление ...Алгоритм решения задачи на нахождение целого и частей
. Тимошенкова. Ирина Викторовна. Учитель начальных классов. МБ НОУ «Гимназия № 70». Г. Новокузнецк. Алгоритм. решения задачи. ...Деление многозначного числа на однозначное число
Тема урока:. Деление многозначного числа на однозначное число. . . Цель:. Систематизировать знания по теме «Деление многозначного числа на однозначное». ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:19 ноября 2018
Категория:Математика
Содержит:30 слайд(ов)
Поделись с друзьями:
Скачать презентацию