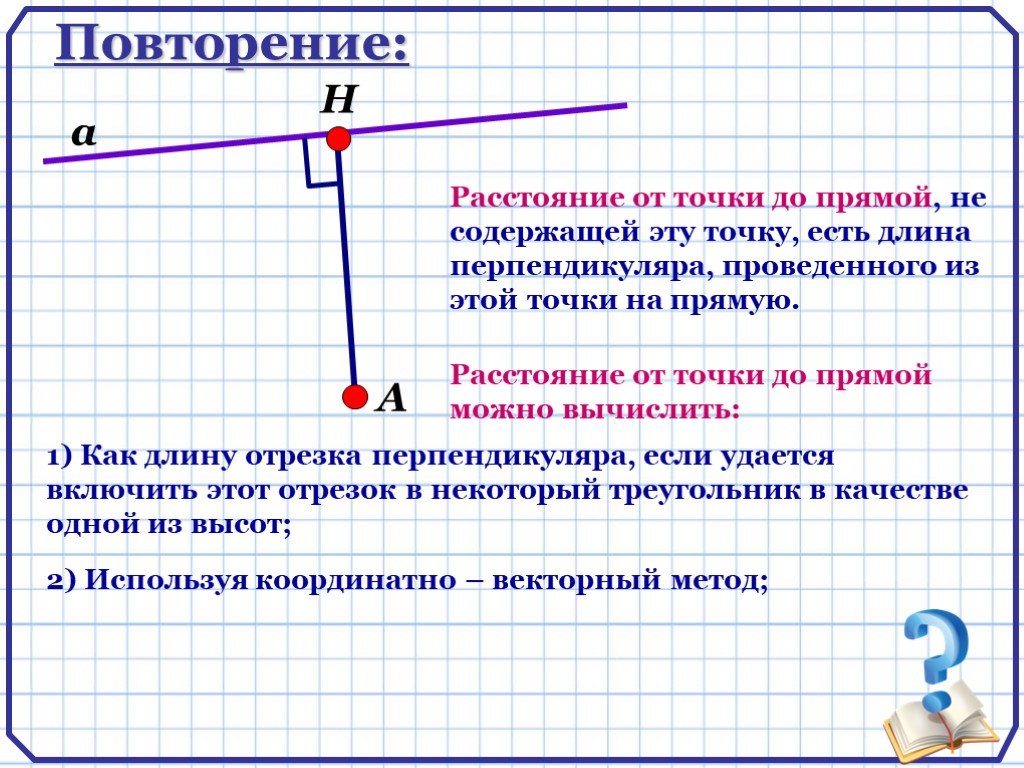
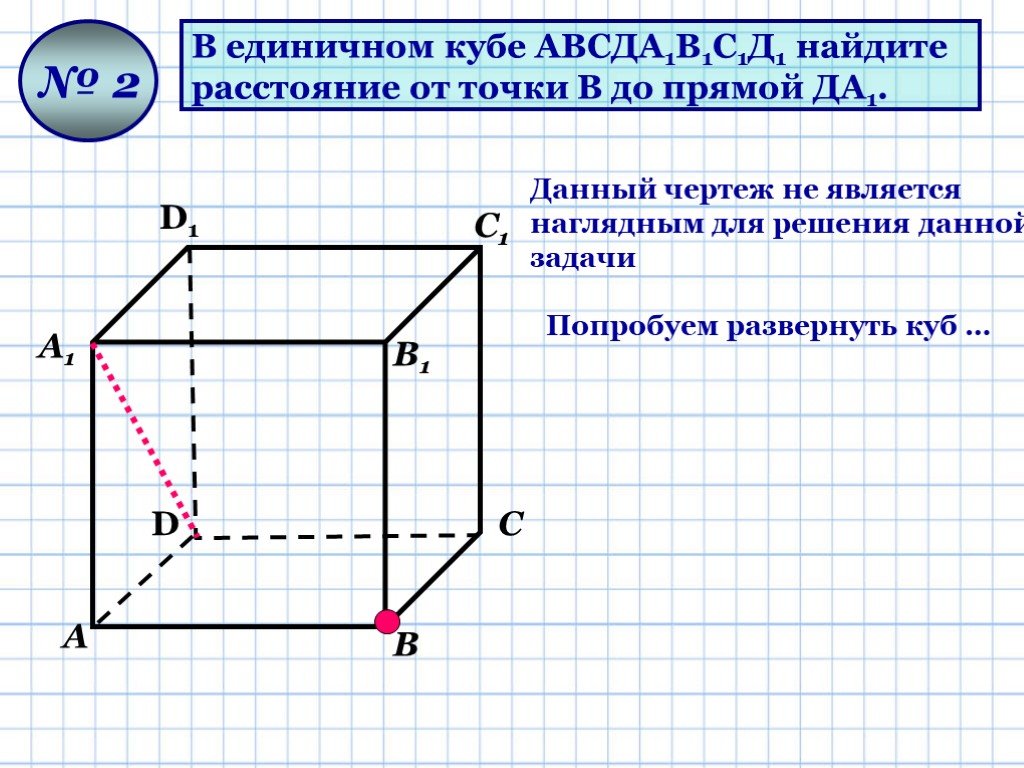
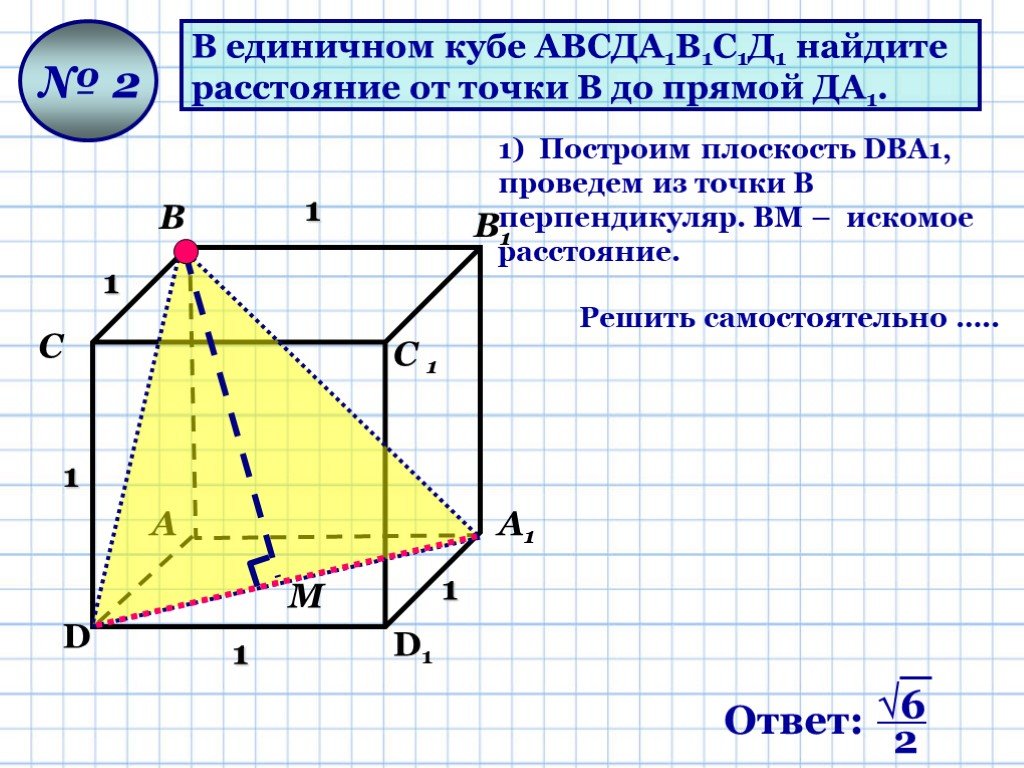
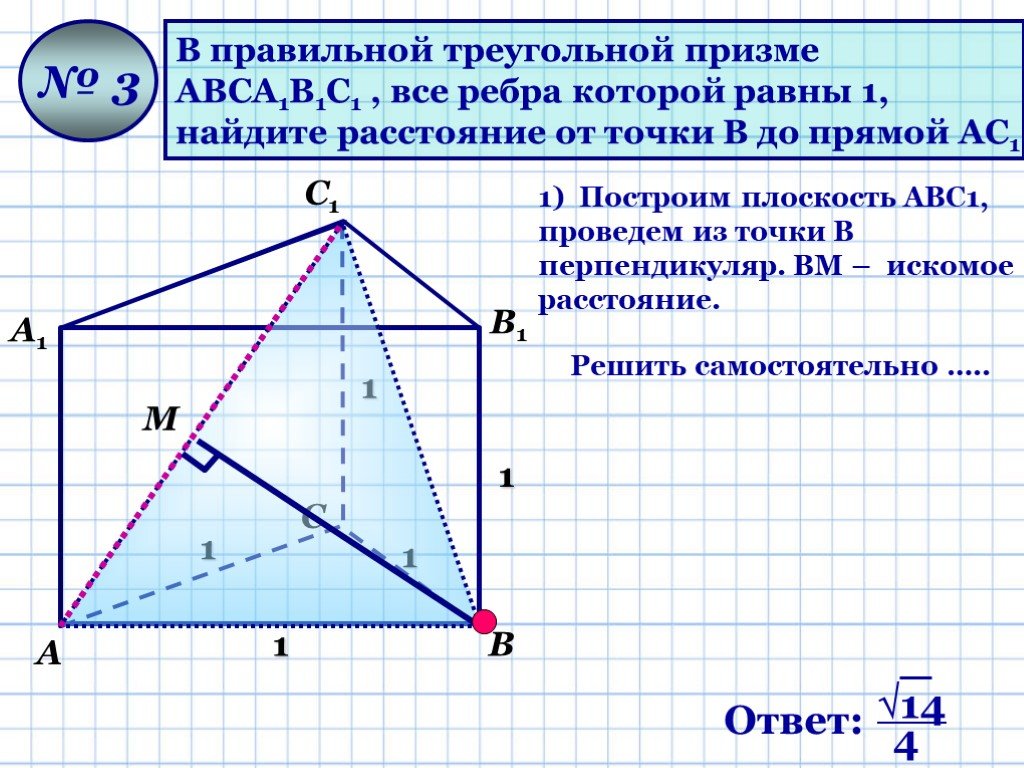
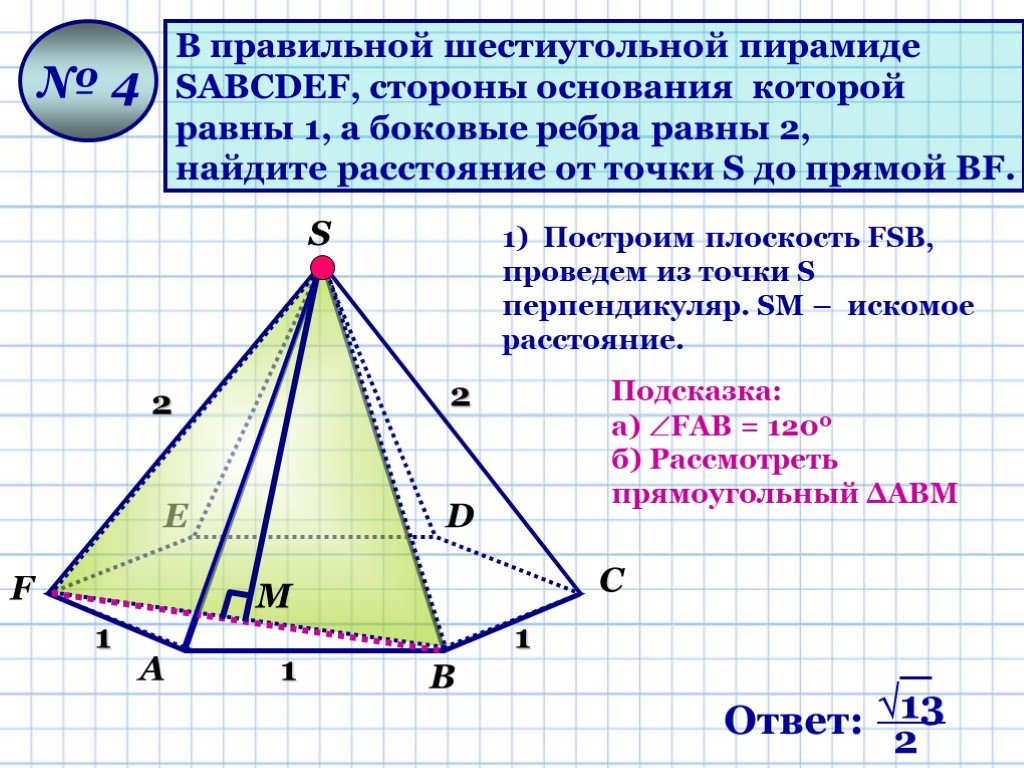
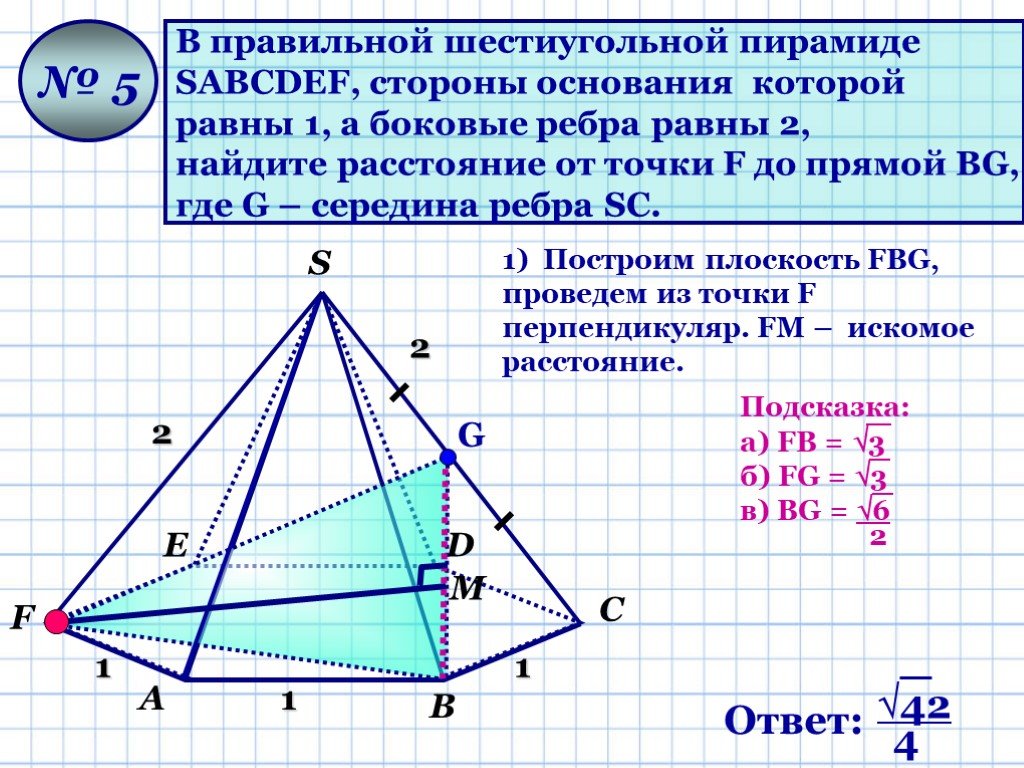
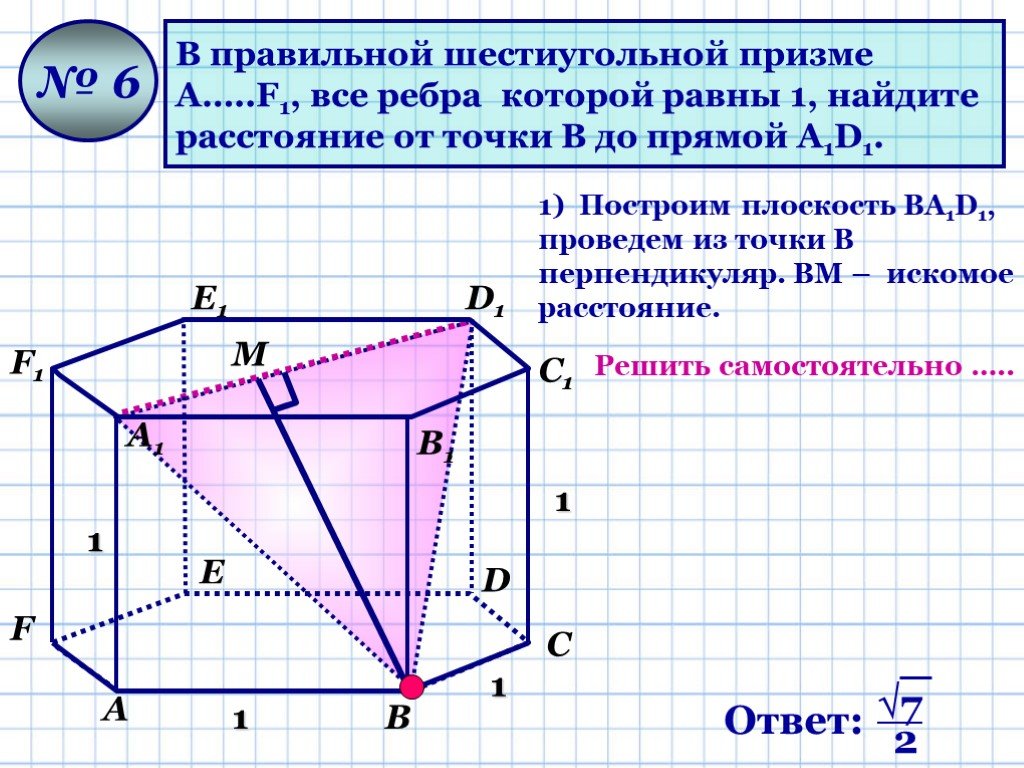
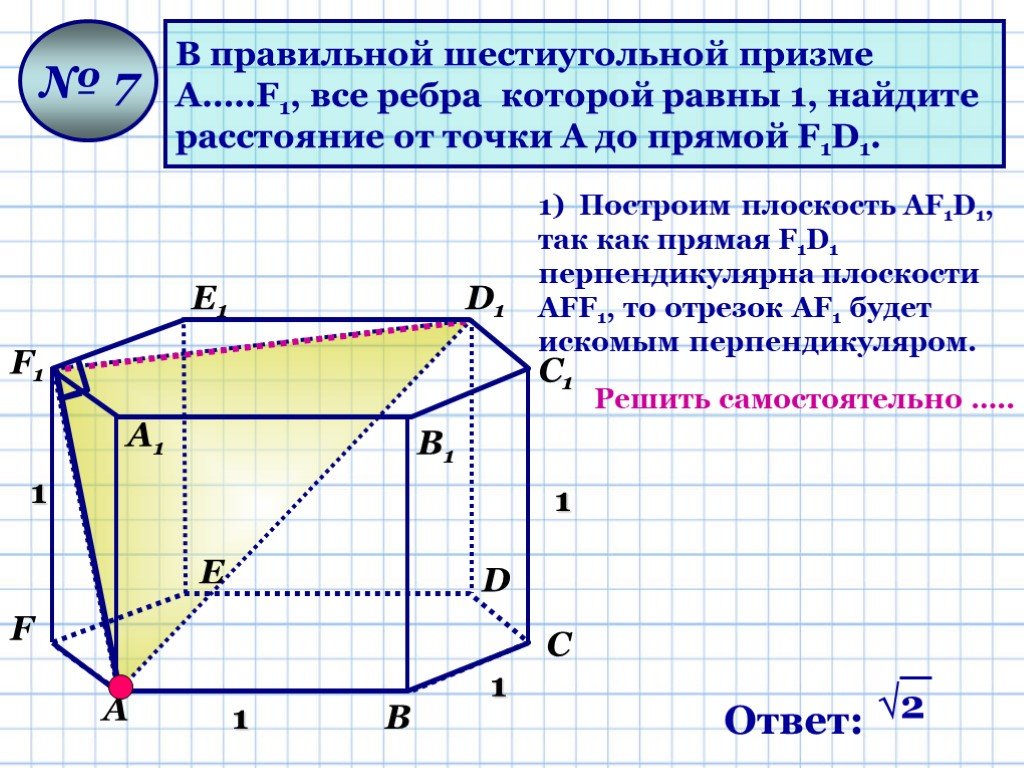
Презентация "Геометрические задачи «С2»" по математике – проект, доклад
Презентацию на тему "Геометрические задачи «С2»" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 17 слайд(ов).
Слайды презентации
Список похожих презентаций
Геометрические задачи со спичками
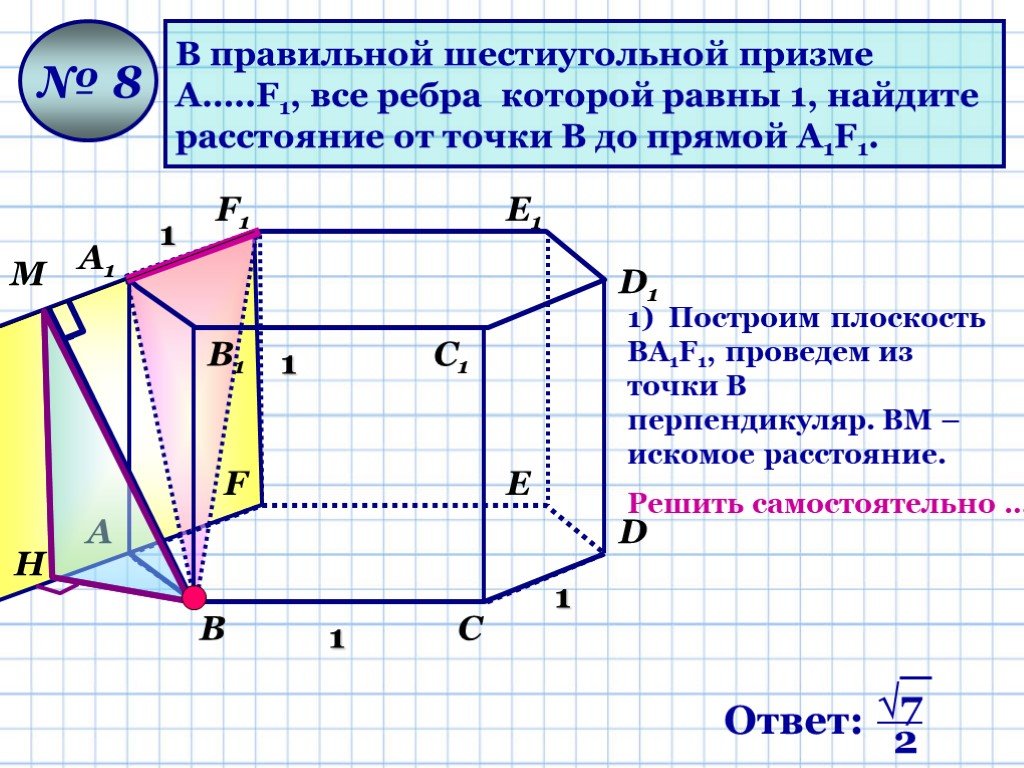
1. Уберите 4 спички так, чтобы осталось 4 маленьких и 1 большой квадраты. Ответ :. 2. От исходного квадрата убрать поочередно 4, 6, 8 спичек так, ...Геометрические задачи типа «С4»
Задачи Желаю успеха! "Дорогу осилит идущий!". Помните:. В треугольнике АВС АВ=15, ВС = 12, СА = 9. Точка D лежит на прямой ВС так, что BD:DC = 3:8. ...Геометрические задачи на построение
Задачи на построение. Окружность Предложение, в котором разъясняется смысл того или иного выражения или названия, называется определением. Мы уже ...Геометрические задачи на экстремум
Определения. Задачи, где требуется определить условия, при которых некоторая величина принимает наибольшее и наименьшее значение, принято называть ...Геометрические задачи с практическим содержанием
введение. Решение геометрических задач с практическим содержанием позволяет: усилить практическую направленность изучения школьного курса геометрии; ...Геометрические фигуры
Тор. Тор (тороид) — поверхность вращения, получаемая вращением образующей окружности вокруг оси, лежащей в плоскости этой окружности, но не проходящей ...Занимательные логические задачи
1. Судаки. Полтора окуня стоят полтора рубля. Сколько рублей стоят 9 окуней? 9. 2. Яблоки. Как разделить пять яблок между пятью девочками так, чтобы ...Занимательные задачи
Мишка 1 + =. Цыплята 2. Белка и орешки 3. Мышата 4. Синички 5. Клубнички 6. ...задачи вступительных экзаменов
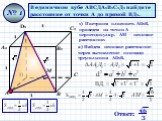
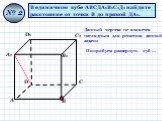
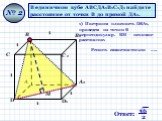
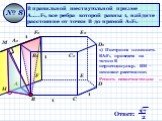
Правильная четырехугольная пирамида. плоскость, проходящая через сторону основания и среднюю линию одной из боковых граней, образует с плоскостью ...Анания Ширакаци и его задачи
Дата рождения: около 610 год Место рождения: в области Ширак провинции Айрарат Дата смерти: около 685 год Научная сфера: математик, астроном, географ. ...Геометрические фигуры вокруг нас
Геометрия возникла очень давно, это одна из самых древних наук. В переводе с греческого слово «геометрия» означает «землемерие» («гео»- по-гречески ...Геометрические фигуры
Результат теста. Верно: 16 Ошибки: 0 Отметка: 5. Время: 1 мин. 0 сек. ещё исправить. С.И. Волкова, И.С. Ордынцева. Математика. Тесты. 2 класс. М., ...Геометрические задания группы В ЕГЭ
Задания группы В4. 1. В треугольнике АВС угол С равен 90°, sin A = 1/7, AC = 4√3. Найдите AB. B A 4√3 C Ответ: 7. 2. В треугольнике АВС угол С равен ...Взаимообратные задачи
Условие Вопрос Схема Выражение Решение Ответ. На кормушке сидело 2 синички. Прилетела ещё 1синичка. Сколько синичек прилетело? На кормушке сидело ...Великие задачи математики. Квадратура круга
Автор: Монахов Станислав. МОУ "Средняя общеобразовательная школа № 59". Курск - 2006. Меня зовут Монахов Станислав. Я ученик 6-го класса, очень люблю ...Вводные задачи
Задачи на чередование. 1.На плоскости располо- жено 11 шестеренок,со- единенных по цепочке. Могут ли все шестеренки вращаться одновременно? Ответ:нет.Если ...Введение понятия "Задачи. Составные части задачи
4. 10. . . 3. Проверьте! 4 10 5 6 3 3 4 5 6 10. Что отсутствует у нашего солнышка, а в математике учит считать? Учит луч! 1 2 5 6 7 8 9 0+1 1+1 2+1 ...Геометрические фигуры
. Тема:. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ. ПРЯМОУГОЛЬНИКИ. ЧЕТЫРЁХУГОЛЬНИКИ. ТРЕУГОЛЬНИКИ. . . . . ЗНАЮ! ТРУДНО! ПОМОГИТЕ! ...Геометрические фигуры на плоскости
Цели урока. Вспомнить изученные геометрические фигуры и их свойства Убедиться в том, что геометрия не просто школьный предмет, а наука, на которой ...Конспекты
Упражнения и задачи на усвоение таблицы деления на 2. Закрепление
Урок математики во 2 классе. Тема: Упражнения и задачи на усвоение таблицы деления на 2. Закрепление . . Урок - закрепление. Цели:. -Воспроизводить ...Решение задачи исследовательского характера
Лукашова Маргарита Александровна, учитель математики МБОУ г. Мурманска лицей №4. . Предмет: математика. Возраст детей: 7 класс. Место проведения: ...Составление краткой записи условия задачи
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа №2. им. А. А. Араканцева г. Семикаракорска». Конспект ...Развивающие задачи
МЕТОДИЧЕСКАЯ РАБОТА. «Развивающие задачи в 5-х классах». Учителя математики высшей квалификационной категории. Васильевой Н. И. ГБОУ СОШ № ...Решаем задачи
Математика: «. Решаем задачи». Цели. :. закрепление навыков решения задач в 1 действие на сложение и вычитание. Задачи:. . Обобщить полученные ...Простейшие вероятностные задачи
Замечательно, что наука, которая начала с рассмотрения азартных игр, обещает стать наиболее важным объектом человеческого знания. Ведь большей частью ...Простые арифметические задачи на разностное сравнение
Тема урока. : «Простые арифметические задачи на разностное сравнение». Тип урока. : урок выработки умений и навыков (применение знаний в новых ситуациях). ...Геометрические фигуры
. План-конспект урока по математике. Тема урока. : «Геометрические фигуры». Тип урока. : обобщающий урок. Цели урока. :. . I. .Образовательно–развивающие ...Геометрические фигуры
Муниципальное бюджетное общеобразовательное учреждение. «Симская средняя общеобразовательная школа». Юрьев – Польского района Владимирской области. ...Геометрические фигуры
Конспект занятия. Тема занятия: «Геометрические фигуры». Тип занятия: З. анятие закрепления знаний. Цель:. формирование умения различать геометрические ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:11 августа 2019
Категория:Математика
Содержит:17 слайд(ов)
Поделись с друзьями:
Скачать презентацию