Презентация "Геометрические задачи типа «С4»" по математике – проект, доклад
Презентацию на тему "Геометрические задачи типа «С4»" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 14 слайд(ов).
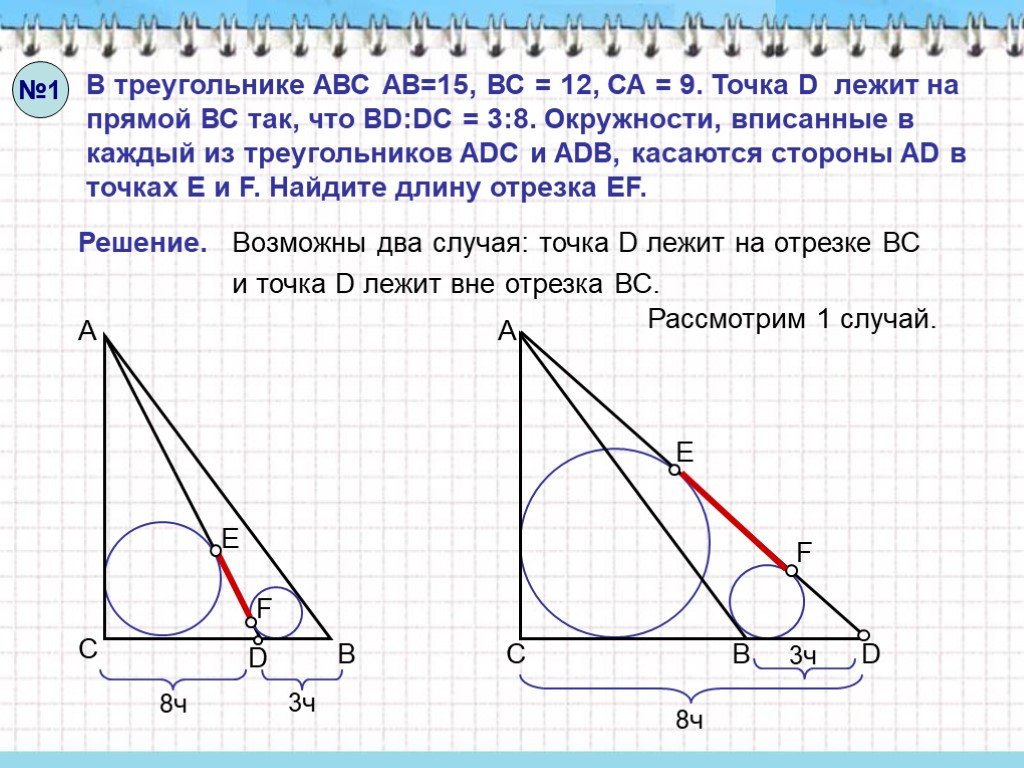
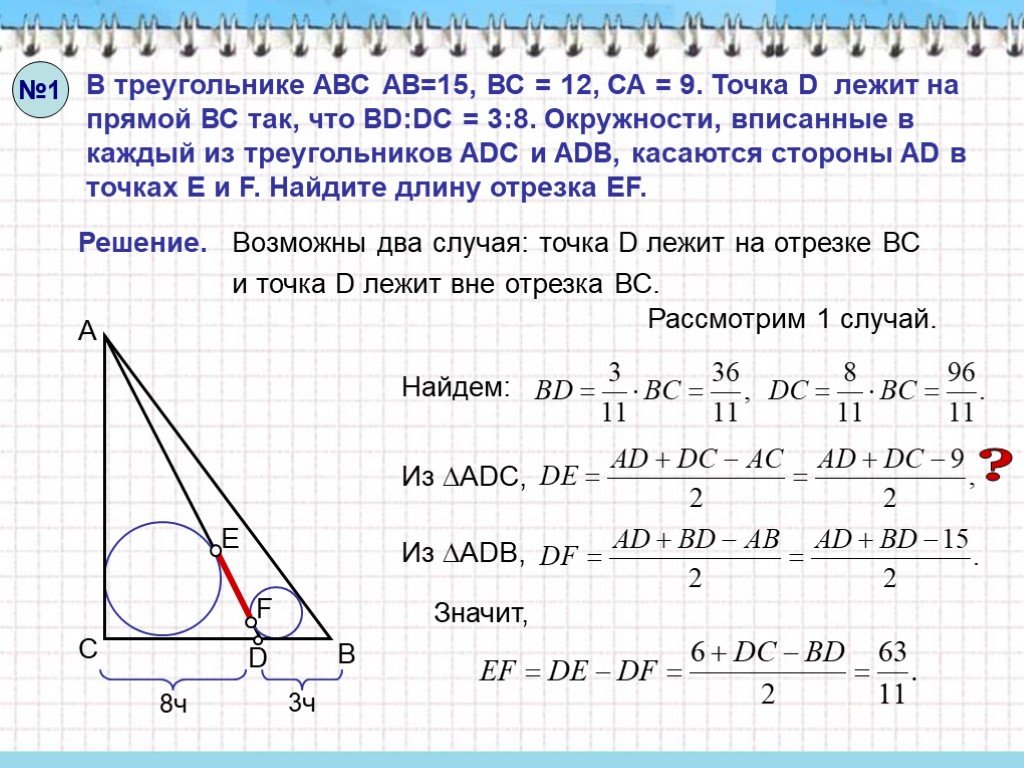
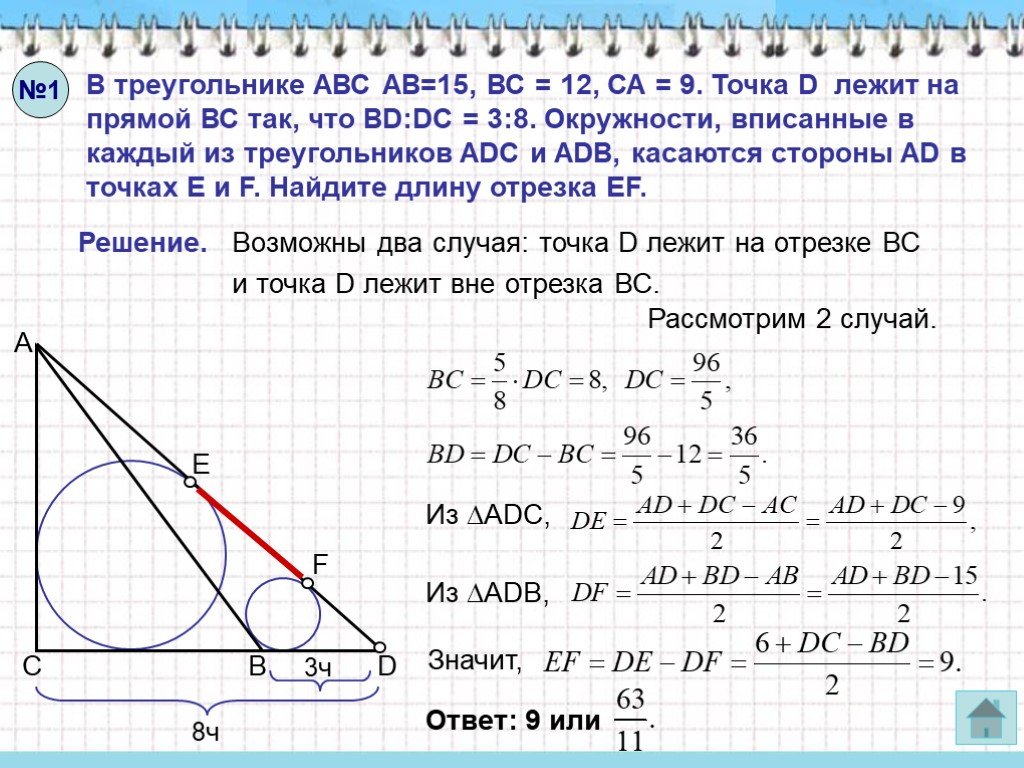
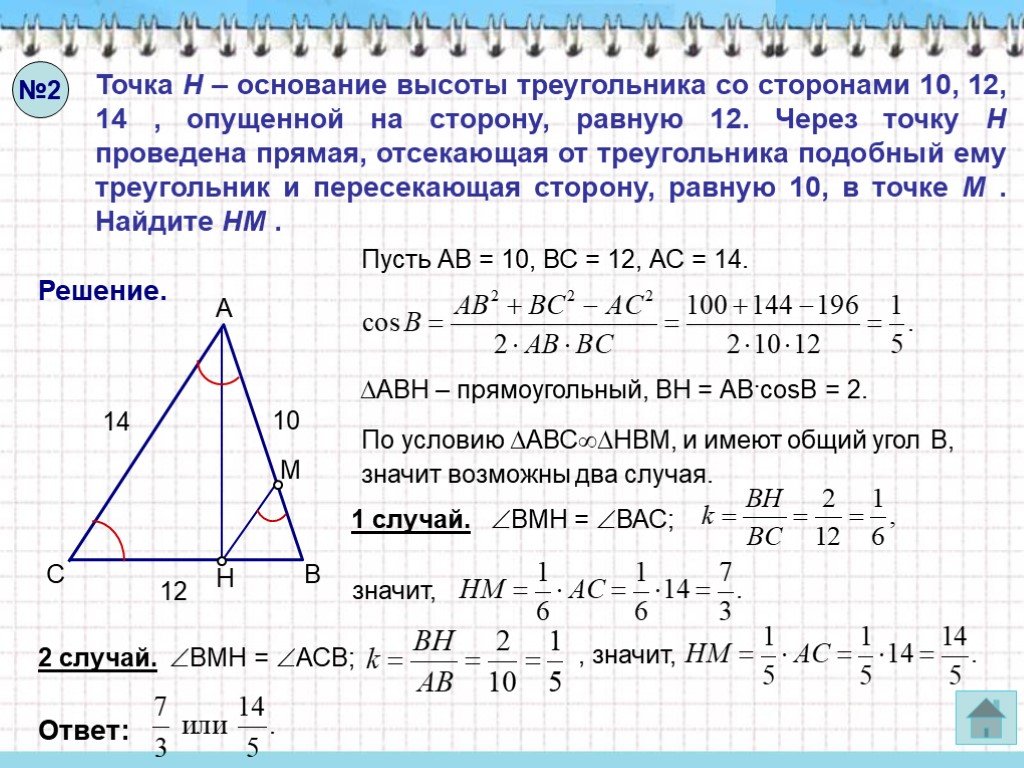
Слайды презентации
Список похожих презентаций
Геометрические задачи с практическим содержанием
введение. Решение геометрических задач с практическим содержанием позволяет: усилить практическую направленность изучения школьного курса геометрии; ...Геометрические задачи со спичками
1. Уберите 4 спички так, чтобы осталось 4 маленьких и 1 большой квадраты. Ответ :. 2. От исходного квадрата убрать поочередно 4, 6, 8 спичек так, ...Геометрические задачи «С2»
«Недостаточно лишь понять задачу, необходимо желание решить ее. Без сильного желания решить трудную задачу невозможно, но при наличии такового возможно. ...Геометрические задачи на построение
Задачи на построение. Окружность Предложение, в котором разъясняется смысл того или иного выражения или названия, называется определением. Мы уже ...Геометрические задачи на экстремум
Определения. Задачи, где требуется определить условия, при которых некоторая величина принимает наибольшее и наименьшее значение, принято называть ...Геометрические фигуры
Тор. Тор (тороид) — поверхность вращения, получаемая вращением образующей окружности вокруг оси, лежащей в плоскости этой окружности, но не проходящей ...Занимательные логические задачи
1. Судаки. Полтора окуня стоят полтора рубля. Сколько рублей стоят 9 окуней? 9. 2. Яблоки. Как разделить пять яблок между пятью девочками так, чтобы ...Занимательные задачи
Мишка 1 + =. Цыплята 2. Белка и орешки 3. Мышата 4. Синички 5. Клубнички 6. ...задачи вступительных экзаменов
Правильная четырехугольная пирамида. плоскость, проходящая через сторону основания и среднюю линию одной из боковых граней, образует с плоскостью ...Анания Ширакаци и его задачи
Дата рождения: около 610 год Место рождения: в области Ширак провинции Айрарат Дата смерти: около 685 год Научная сфера: математик, астроном, географ. ...Геометрические фигуры вокруг нас
Геометрия возникла очень давно, это одна из самых древних наук. В переводе с греческого слово «геометрия» означает «землемерие» («гео»- по-гречески ...Геометрические фигуры
Результат теста. Верно: 16 Ошибки: 0 Отметка: 5. Время: 1 мин. 0 сек. ещё исправить. С.И. Волкова, И.С. Ордынцева. Математика. Тесты. 2 класс. М., ...Геометрические задания группы В ЕГЭ
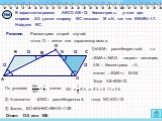
Задания группы В4. 1. В треугольнике АВС угол С равен 90°, sin A = 1/7, AC = 4√3. Найдите AB. B A 4√3 C Ответ: 7. 2. В треугольнике АВС угол С равен ...Взаимообратные задачи
Условие Вопрос Схема Выражение Решение Ответ. На кормушке сидело 2 синички. Прилетела ещё 1синичка. Сколько синичек прилетело? На кормушке сидело ...Великие задачи математики. Квадратура круга
Автор: Монахов Станислав. МОУ "Средняя общеобразовательная школа № 59". Курск - 2006. Меня зовут Монахов Станислав. Я ученик 6-го класса, очень люблю ...Вводные задачи
Задачи на чередование. 1.На плоскости располо- жено 11 шестеренок,со- единенных по цепочке. Могут ли все шестеренки вращаться одновременно? Ответ:нет.Если ...Введение понятия "Задачи. Составные части задачи
4. 10. . . 3. Проверьте! 4 10 5 6 3 3 4 5 6 10. Что отсутствует у нашего солнышка, а в математике учит считать? Учит луч! 1 2 5 6 7 8 9 0+1 1+1 2+1 ...Геометрические фигуры
. Тема:. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ. ПРЯМОУГОЛЬНИКИ. ЧЕТЫРЁХУГОЛЬНИКИ. ТРЕУГОЛЬНИКИ. . . . . ЗНАЮ! ТРУДНО! ПОМОГИТЕ! ...Геометрические фигуры на плоскости
Цели урока. Вспомнить изученные геометрические фигуры и их свойства Убедиться в том, что геометрия не просто школьный предмет, а наука, на которой ...Конспекты
Текстовые задачи в два действия
Конспект урока математики по УМК «Школа России» ФГОС. Класс:. 1-А. Учитель:. Примак Т.М. Тип урока:. урок «открытия» нового знания. Тема урока:. ...Решение задач. Вычисление и запись ответа задачи
Математика 1 класс. Тема: Решение задач. Вычисление и запись ответа задачи. Цели:. . Образовательная. Продолжить работу над задачей, повторить ...Решение примеров и задачи
Урок математики. 2 класс (II. отделение). Тема:. Решение примеров и задачи. Цели. :. . Обучающая. . Закреплять умение складывать и ...Разбиение текста задачи на условие и вопрос
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа № 18». г. Абакана Республики Хакасия. ...Решаем задачи
Конспект урока математики в 1 классе с учетом ФГОС. Составлен учителем высшей категории МАОУ гимназия №16 Козловой М.А. Тема урока: «. Решаем ...Приём устного деления двузначного числа на однозначное. Решение учебной задачи
. КОНСПЕКТ УРОКА по ФГОС. Предмет:. математика (УМК «Гармония»). Класс: 3 А. . Учитель:. Рамазанова Е.Л. Тема урока:. «. Приём устного деления ...Простые арифметические задачи на определение продолжительности, начала и конца события 7 класс
Простые арифметические задачи на определение продолжительности, начала и конца события. 7 класс. Цели урока:. - Формировать умения решать текстовые ...Геометрические фигуры
Муниципальное бюджетное дошкольное образовательное учреждение. «Детский сад комбинированного вида №22 «Солнышко». Конспект урока ...Геометрические фигуры
. План-конспект урока по математике. Тема урока. : «Геометрические фигуры». Тип урока. : обобщающий урок. Цели урока. :. . I. .Образовательно–развивающие ...Геометрические фигуры
1 класс – интегрированный урок (математика и трудовое обучение). Тема: «Геометрические фигуры». Цель: закрепление знаний о геометрических, пространственных ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:12 августа 2019
Категория:Математика
Содержит:14 слайд(ов)
Поделись с друзьями:
Скачать презентацию